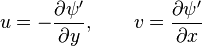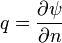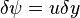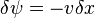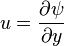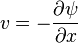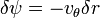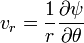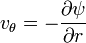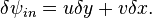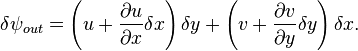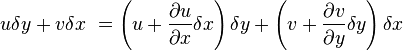Akım fonksiyonu
Akım Fonksiyonu çeşitli iki boyutlu akışlar için ifade edilir. Akım fonksiyonu, kararlı akıştaki partiküllerin yörüngelerini gösteren akım çizgileri, çıkış çizgileri ve yörüngeyi çizmek için kullanılabilir. Akım çizgileri eş potansiyel çizgilerine diktir.
Herhangi iki noktadaki akım fonksiyonu değeri arasındaki fark, aynı iki noktayı birbirine bağlayan hat boyunca var olan hacimsel akış oranını (hacimsel akı) verir.
Akım çizgileri akıştaki hız vektörlerine teğet olduğu için, akım fonksiyonunun değeri akım çizgisi boyunca sabit olmak zorundadır.
Akım fonksiyonunun kullanılabilirliği, verilmiş bir noktadaki x- ve y- yönlerindeki hız bileşenleri, bu noktadaki akım fonksiyonunun kısmi türevleri alınarak bulunur gerçeği altında yatar. Akım fonksiyonu iki veya daha çok boyutlu bir akış için ifade edilebilir. Fakat iki boyutlu durum genellikle hesaplama ve görüntüleme bakımından en kolay olanıdır.
Hız potansiyeli ile birlikte alındığı zamam akım fonksiyonu, potansiyel akışı türetmek için kullanılabilir. Diğer bir değişle, akım fonksiyonu iki boyutlu Helmholtz dekompozisyonunun selonoidal kısmını ifade ederken, hız potansiyeli ise irrotasyonel kısmını ifade eder.
İki Boyutlu Akım Fonksiyonu
Tanımlar
Akım fonksiyonunun simgesi kullanılan tanıma göre değişir.
Bunlardan birisi akım fonksiyonunu 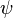 iki boyutlu akış için tanımlamaktır:
iki boyutlu akış için tanımlamaktır:
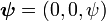 hız vektörü
hız vektörü 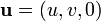 durumunda iken
durumunda iken
Kartezyen koordinat sistemi'nde aşağıdaki eşitlikteki gibidir
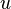 ve
ve 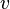 hızları, sırasıyla, kartezyen koordinatlardaki
hızları, sırasıyla, kartezyen koordinatlardaki 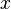 ve
ve 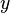 yönlerindeki hızlardır.
yönlerindeki hızlardır.
Alternatif Tanımı
Diğer bir tanımı ise şöyledir (genellikle meteoroloji ve okyanus biliminde kullanılır):
 ,
,
 ,
, 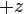 yönündeki birim vektördür ve and alt indisler kısmi türevleri belirtir.
yönündeki birim vektördür ve and alt indisler kısmi türevleri belirtir.
Burada kullanılan tanım, yukarıdakine göre ters işarete sahiptir(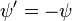 ), böylelikle kartezyen koordinatlardaki biçimi şöyledir
), böylelikle kartezyen koordinatlardaki biçimi şöyledir
İki Boyutlu Akım Fonksiyonunun Türevi
İki boyutlu düz bir akışta A ve B gibi iki farklı nokta farzedin. Eğer bu iki nokta arası uzaklık çok küçükse: δn, ve bir akış bu iki noktalar arasında ortalama bir hızla hareket eder. q AB çizgisine diktir. Birim kalınlık başına düşen hacimsel akış oranı δΨ:
δn → 0, (δn sıfıra yaklaştıkça) yukarıdaki eşitlik düzenlenirşe şunu elde etmiş oluruz:
Kartezyen Koordinatlardaki Akış
x-y kartezyen koordinat sistemindeki elementer bir alan içindeki akışı incelediğimizde şunu elde ederiz:
u hızı x eksenine paralel, v ise y eksenine paralel hızdır. Bu yüzden, δn → 0 yaklaştıkça:
Polar Koordinatlardaki Akış
r-θ polar koordinat sistemindeki çok küçük bir bölgeyi incelersek:
vr r eksenine paralel radyal hız bileşeni, vθ ise θ eksenine paralel teğetsel hız vektörüdür. Böylece, δn → 0 gittikçe ve eşitlik yeniden düzenlenince:
Süreklilik: Türev
Kartezyen koordinatlarda iki boyutlu düz bir akış düşünün. Süreklilik denklemi; elementer bir bölge içinde sıkıştırılamaz bir akış için, çıkan kütle giren kütleye eşittir.
Toplam akış aşağıdaki ifadeyle verilir:
Kontrol hacmi dışına çıkan toplam akış:
Böylelikle:
sadeleştirirsek:
Akım fonksiyonunun tanımı itibariyle yukarıdaki eşitliği birleştirirsek:
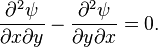 bulmuş oluruz
bulmuş oluruz
Kaynaklar
- B. S. Massey and J. Ward-Smith, Mechanics of Fluids, 7th ed., Nelson Thornes, UK (1998).
- F. M. White, Fluid Mechanics, 5th ed., McGraw-Hill, New York (2003).
- T. W. Gamelin, Complex Analysis, Springer, New York (2001). ISBN 0-387-95093-1.
- AMS Glossary of Meteorology entry: