Atış hareketi

Suyun parabolik yörüngesi

Eğik atışta ilk hız

İlk hızın bileşenlerine ayrılması

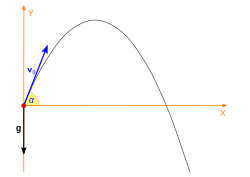
Atış hareketi, Dünya yüzeyine yakın yerlerde; düşen, fırlatılan cisimlerin yaptığı harekettir. Bu harekette cismin ivmesi sabittir ve yerçekimi ivmesine eşittir.

İlk hız

Eğer cisim belli bir v₀ ilk hızı ile atılırsa bu hız birim vektörler cinsinden aşağıdaki gibi yazılabilir.

${\displaystyle \mathbf {v} _{0}=v_{0x}\mathbf {i} +v_{0y}\mathbf {j} }$

Bileşenler, birim vektörler dışında, yatayla yapılan θ açısı cinsinden de yazılabilir:

${\displaystyle v_{0x}=v_{0}\cos \theta }$,

${\displaystyle v_{0y}=v_{0}\sin \theta }$.

Eğer cismin menzili, fırlatılma açısı ve maksimum yüksekliği biliniyorsa; ilk hız aşağıdaki gibi yazılabilir.

${\displaystyle V_{0}={\sqrt {{R^{2}g} \over {R\sin 2\theta +2h\cos ^{2}\theta }}}}$.

Kinematik nicelikler

Atış hareketi, sabit hızlı yatay hareketin ve sabit ivmeli düşey hareketin bir birleşimidir. Yatay ve düşeydeki hareketin formülleri birbirinden bağımsızdır.

İvme

Yatay harekette ivme yoktur, bu yüzden hız sabit ve v₀cos θ ya eşittir. Düşey hareketteyse ivme sabittir ve g'ye eşittr. Böylece ivmenin bileşenleri şu şekilde yazılır:

${\displaystyle a_{x}=0}$,

${\displaystyle a_{y}=-g}$.

Hız

Yatayda ivme olmadığı için cismin yatay hızı değişmez. Düşeyde ise cisim yükseliyorsa hız azalır, düşüyorsa artar. Herhangi bir t anında cismin hızları şu şekildedir:

${\displaystyle v_{x}=v_{0}\cos(\theta )}$,

${\displaystyle v_{y}=v_{0}\sin(\theta )-gt}$.

Cismin toplam hızı Pisagor teoremi yardımıyla şu şekilde bulunur:

${\displaystyle v={\sqrt {v_{x}^{2}+v_{y}^{2}\ }}}$.

Yerdeğiştirme

Eğik atışta koordinatlar ve yerdeğiştirme

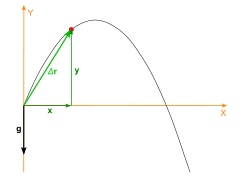
Atılma noktası orijin kabul edilirse, atılan cismin zamana bağlı koordinatları şu şekildedir:

${\displaystyle x=v_{0}t\cos(\theta )}$,

${\displaystyle y=v_{0}t\sin(\theta )-{\frac {1}{2}}gt^{2}}$.

Yerdeğiştirmenin büyüklüğü:

${\displaystyle \Delta r={\sqrt {x^{2}+y^{2}\ }}}$.

Parabolik yörünge

Cismin konumunun zaman parametresine bağlı denklemi şudur:

${\displaystyle x=v_{0}t\cos(\theta )}$,

${\displaystyle y=v_{0}t\sin(\theta )-{\frac {1}{2}}gt^{2}}$.

Zamandan bağımsız bir konum denklemi yazılmak istenirse şu şekilde olur:

${\displaystyle y=\tan(\theta )\cdot x-{\frac {g}{2v_{0}^{2}\cos ^{2}\theta }}\cdot x^{2}}$,

Burada, g, θ ve v sabittir. Dolayısıyla fonksiyonun grafiği parabol şeklindedir. Bu da atış hareketinde yörüngenin parabolik olduğunu gösterir.

Atılan cisim parabol çizerek ileryeceği için

θ = atış açısı

h= maxsimum yükseklik

x = maksimum yükseliğe ulaştığı noktanın yatay uzaklığı (menzilin yarısı)

θ=arctan(2h/x) olur.

Maksimum yükseklik

Maksimum yükseklik h

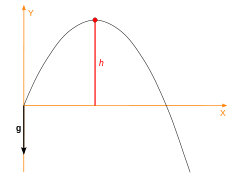
Yerden eğik atılan bir cisim maksimum yüksekliğe çıktığında düşey hızı ${\displaystyle v_{y}=0}$ olur. Kinematik denklemleri kullanılırsa:

${\displaystyle 0=v_{0}\sin(\theta )-gt_{h}}$.

Bu yüksekliğe çıkış süresi

${\displaystyle t_{h}={v_{0}\sin(\theta ) \over g}}$.

Buradan maksimum yükseklik şu bulunur:

${\displaystyle h=v_{0}t_{h}\sin(\theta )-{\frac {1}{2}}gt_{h}^{2}}$

${\displaystyle h={v_{0}^{2}\sin ^{2}(\theta ) \over {2g}}}$ .

Kaynakça

• "Atış Simülasyonu". 11 Aralık 2013 tarihinde kaynağından arşivlendi. http://web.archive.org/web/20131211084514/http://www.meb.gov.tr/duyurular/duyurular2008/egitek/webII/ogrenci_fen/1/Atislar.swf. Erişim tarihi: 6 Aralık 2013. 
• Harran Üniversitesi. "Düzlemsel Hareket". 10 Aralık 2013 tarihinde kaynağından arşivlendi. http://web.archive.org/web/20131210213856/http://eng.harran.edu.tr/moodle/moodledata/47/Ders_Notlari/Bolum_6.pdf. Erişim tarihi: 6 Aralık 2013. 
• Ankara Üniversitesi. "İki Boyutta Hareket". 18 Temmuz 2013 tarihinde kaynağından arşivlendi. http://web.archive.org/web/20130718065243/http://acikders.ankara.edu.tr/pluginfile.php/281/mod_resource/content/1/iki%20boyutta%20hareket%20.pdf. Erişim tarihi: 6 Aralık 2013.