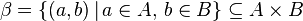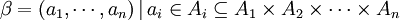Bağıntı

Matematikte iki kümenin Kartezyen çarpımının herhangi bir alt kümesi bağıntı olarak tanımlanır. Bir kümedeki bir öğeyi başka bir kümedeki bir öğeye götürür. Yâni, iki öğe arasında bir bağ kurar. Örneğin, göndermeler tek yönlü bir bağıntıdır.

Tanım

A ve B herhangi iki küme olsun. 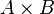$A \times B$'nin herhangi bir altkümesine bağıntı denir:

(2)İki ya da daha çok şey arasındaki karşılıklı ilişki, ilinti.

Eşyayı, kavramları ya da tasarımları birlik, bağlılık, birliktelik gibi durumlarda toplayan görünüş ya da nitelik, görelik, °izafiyet, °rölativite.

$\beta=\{(a,b) \, | \, a \in A, \, b \in B \} \sube A \times B$

burada a ile b öğeleri arasında bir bağ vardır. Dikkat edilirse bir bağıntı boş olabilir. Çünkü kümedeki öğelerin varlığından söz edilmiyor, eğer 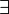$\exist$ simgesi olsaydı o zaman öğelerin varlığı zorunlu olurdu. Boşküme de kartezyen uzayın bir altkümesi olduğu için boş bağıntı mümkündür.

Daha genel olarak, birbirinden farklı olması gerekmeyen n küme (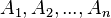$A_1, A_2, ..., A_n$) arasındaki n 'li bağıntı (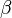$\beta$), bu kümelerin kartezyen çarpımının herhangi bir alt kümesidir.

$\beta = {(a_1, \cdots, a_n) \, | \, a_i \in A_i} \subseteq A_1 \times A_2 \times \cdots \times A_n$

n, iki ise ikili bağıntı olarak adlandırılır.

Örnekler

Evlilik ilişkisi

A={Ayşe, Fatma, Esra, Ali, Veli, Ahmet, Mehmet}

A ile A arasındaki hayali bir evlilik ilişki (E) aşağıdaki gibi olabilir:

E={(Ayşe, Ali), (Ali, Ayşe), (Esra, Mehmet), (Mehmet, Esra)}

Buna göre A kümesinin elemanlarından, Ayşe ve Ali, Esra ve Mehmet evlidir.

Yaşça büyüklük ilişkisi

Bütün ilişkiler simetrik olmak zorunda değildir. Örneğin K kümesinden, yaşça büyüklük ilişkisi (B) şöyle olabilir.

K={Ayşe, Fatma, Esra}

B={(Fatma, Ayşe), (Fatma, Esra), (Esra, Ayşe)}

Bu ilişkiye göre yaş sıralaması büyükten küçüğe Fatma, Esra, Ayşe şeklindedir.

Ayrıca bakınız

• Küme
• Denklik bağıntısı
• Sıralama bağıntısı
• Gönderme (Fonksiyon)
• İlişkisel cebir