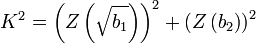D'Agostino'nun K-kare sınaması
İstatistik bilim dalında D'Agostino'nun K2 sınaması normal dağılımdan ayrılmayı ölçmek için kullanılan bir uygulama iyiliği ölçüsüdür. Örneklem basıklık ve çarpıklık ölçülerinin dönüşümlerinden elde edilmiştir. K2 istatistiği şöyle elde edilir:
n değerinin gözlem sayısı ve böylelikle genellikle serbestlik derecesi olduğu bilinmektedir. Örneklem çarpıklık ölçüsü, 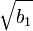 , şöyle tanımlanır:
, şöyle tanımlanır:
Örneklem basıklık ölçüsü, 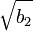 ise şöyle tanimlanır:
ise şöyle tanimlanır:
Burada  örneklem ortalaması, σ2 ikinci merkezsel moment veya varyans ve sırasiyla μ3 ve μ4 üçüncü ve dördüncü merkezsel moment lerdir.
örneklem ortalaması, σ2 ikinci merkezsel moment veya varyans ve sırasiyla μ3 ve μ4 üçüncü ve dördüncü merkezsel moment lerdir.
Dönüştürülmüş çarpıklık
Önce, çarpıklık ölçüsü 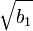 'nin bir dönüşümü olan
'nin bir dönüşümü olan
hesaplanır. Verinin normal dağılım gösterdiğine dair sıfır hipotez geçerli ise, bu ifade yaklaşık olarak normal dağılım gösterir:
Dönüştürülmüş Basıklık
Sonra, basıklık ölçüsü olan 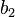 'in bir dönüşümü olan
'in bir dönüşümü olan 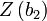 hesaplanır. Verinin normal dağılım gösterdiğine dair sıfır hipotez geçerli ise, bu ifade de yaklaşık olarak normal dağılım gösterir:
hesaplanır. Verinin normal dağılım gösterdiğine dair sıfır hipotez geçerli ise, bu ifade de yaklaşık olarak normal dağılım gösterir:
Bundan sonra ise, basıklık ifadesinin çaprazlığı bulunur:
İçerikli K2 istatistiği
Şimdi, bu 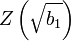 ile
ile 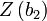 ifadelerini birleştirip normallik sınaması için D'Agustino'nun sinama istatistigi şöyle tanımlanır:
ifadelerini birleştirip normallik sınaması için D'Agustino'nun sinama istatistigi şöyle tanımlanır:
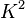 istatistiği yaklaşık olarak serbestlik derecesi 2 olan bir
istatistiği yaklaşık olarak serbestlik derecesi 2 olan bir 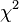 ile dağılım gösterir.
ile dağılım gösterir.
İçsel kaynaklar
- Normallik sınamaları
- Kolmogorov-Smirnov sınaması
- Shapiro-Wilk sınaması
- Smirnov-Cramér-von-Mises sınaması
- Jarque-Bera sınaması
Kaynak
Referanslar
- D'Agostino, Ralph B., Albert Belanger, and Ralph B. D'Agostino, Jr. "A Suggestion for Using Powerful and Informative Tests of Normality", The American Statistician, Cilt. 44, No. 4. (Kasım., 1990), say. 316-321.
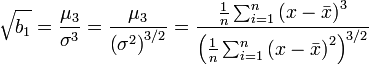
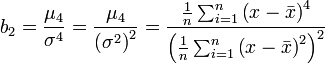
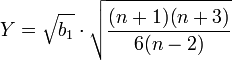
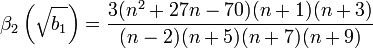
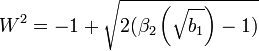
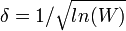
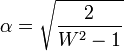
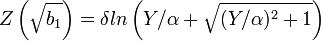
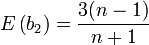
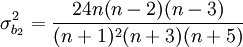
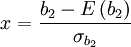
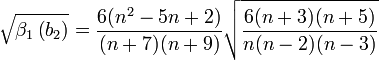
![A = 6 + \frac{8}{\sqrt{\beta_1\left(b_2\right)}} \left[ \frac{2}{\sqrt{\beta_1\left(b_2\right)}} + \sqrt{1+\frac{4}{\beta_1\left(b_2\right)}}\right]](../I/m/f07c7ef9bda42c71a718aa0e2e8be4ea.png)
![Z\left(b_2\right) = \left(\left(1 - \frac{2}{9A}\right) - \sqrt[3]{\frac{1-2/A}{1+x\sqrt{2/(A-4)}}}\right)\sqrt{\frac{9A}{2}}](../I/m/0ee250958e8fe6441267ea66c288ad25.png)