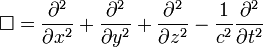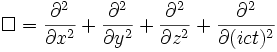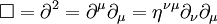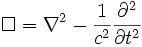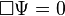D'Alembert işleci

D'Alembert İşlemcisi, Özel görelilikte, elektromanyetizmada ve dalga kuramında; Minkowski uzayını ve Einstein alan denklemlerinin diğer çözümlerini sağlayan Laplace işlemcisine d'Alembert işlemcisi veya dalga işlemcisi denir.

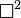İşlemci, $\square$ ya da $\square^2$ olarak da gösterilebilir. Kare olmasının nedeni 4 boyutlu Minkowski uzayını temsil ediyor olmasıdır. Aynı şekilde Laplace işlemcisindeki 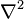$\nabla^2$ simgesi de 3 boyutlu uzayı temsil etmektedir. Kuantum alan kuramında daha çok 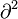$\partial^2$ gösterimi yeğlenir.

Tanım

Minkowski uzayında d'Alembert işlemcisinin açık tanımı, c ışık hızı olmak üzere,

$\square = {\partial^2 \over \partial x^2 } + {\partial^2 \over \partial y^2 } + {\partial^2 \over \partial z^2 } - \frac {1}{c^2}{\partial^2 \over \partial t^2 }$

şeklindedir. Burada açıkça görüleceği gibi uzay 4 boyutludur. Ancak sâdelik adına (x,y,z,t) koordinatları yerine (x,y,z,ict) seçilerek,

$\square = {\partial^2 \over \partial x^2 } + {\partial^2 \over \partial y^2 } + {\partial^2 \over \partial z^2 } + {\partial^2 \over \partial (ict)^2 }$

biçimine dönüşür. Burada i sanal birim]dir.

Einstein toplam uzlaşımı ile 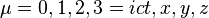$\mu={0,1,2,3}={ict,x,y,z}$ koordinatlar ve 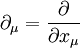$\partial_\mu = {\partial \over \partial x_\mu}$ türevler olmak üzere d'Alembert işlemcisi,

$\square = \partial^2 = \partial^\mu \partial_\mu = \eta^{\nu\mu} \partial_\nu \partial_\mu$

olarak ifâde edilebilir ki burada 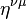$\eta^{\nu\mu}$ Minkowski metriğidir.

Ayrıca Laplace işlemcisi ile de tanımlanabilir:

$\square = \nabla^2 - {1 \over c^2}{\partial^2 \over \partial t^2}$

Fizikte d'Alembert işlemcisi

Dalga denklemi, d'Alembert işlemcisi ile ifâde edilebilir:

$\square \Psi=0$

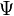burada $\Psi$ dalga fonksiyonudur.