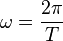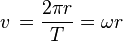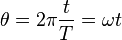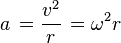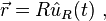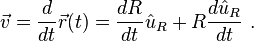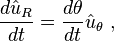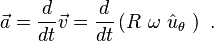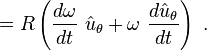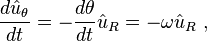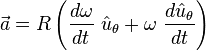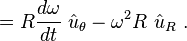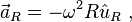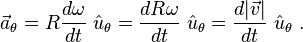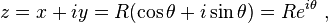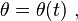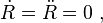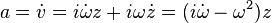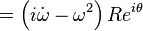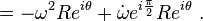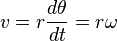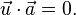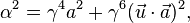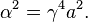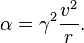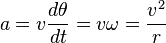Dairesel hareket
Fizikte, dairesel hareket bir nesnenin dairesel bir yörünge boyunca bir rotasyon ya da çemberin çevresinde yaptığı harekettir. Rotasyonun (ve sürekli hızın) sürekli açısal değeriyle birlikte düzgün ya da değişen rotasyon değeriyle düzensiz olabilir. 3 boyutlu bir cismin sabit ekseni etrafındaki rotasyon parçalarının dairesel hareketini içerir. Hareketin denkliği bir cisim kütlesinin merkezini tanımlar.
Dairesel hareketin örnekleri şunları içerir: sabit ağırlıkta Dünya yörüngesinde dönen yapay bir uydu, bir ipe bağlanmış ve daireler şeklinde sallanan bir taş, parkurda viraj boyunca dönen bir araba, düzgün bir manyetik alana dikey olarak hareket eden bir elektron ve bir mekanizmanın içerisinde dönen bir dişli. Nesnenin sürat vektörü sürekli yön değiştirdiği için, hareket eden nesne rotasyon merkezinin yöndeki merkezcil bir kuvvet tarafından ivme kazandırılıyor. Newton’un hareket yasalarına göre bu ivme olmadan nesne düz bir çizgide hareket eder.
Üniform
Fizikte, düzgün dairesel hareket dairesel bir yörüngeyi sabit hızla geçen bir cismin hareketini tanımlar. Cisminin rotasyon ekseninden uzaklığı her zaman sabit kalır. Cismin hızının sabit olmasına rağmen, sürati sabit değildir: sürat, vektörel bir büyüklük, hem cismin hızına hem gidiş yönüne bağlıdır. Bu değişken sürat bir ivmenin varlığını gösterir; bu merkezcil ivme düzgün genlikten kaynaklanır ve her zaman rotasyon eksenine doğru yönlendirilir. Bu ivme dolayısıyla aynı şekilde genlikte düzgün ve rotasyon eksenine doğru yönlendirilmiş merkezcil bir güç tarafından üretilir.
Yörüngenin yarıçapına oranla göz ardı edilebilecek küçüklükte olmayan sert bir cismin sabit ekseni etrafındaki rotasyon durumunda, cismin her bir parçacığı aynı açısal sürat fakat konum ve yörüngeye bağlı olarak değişen sürat ve ivmeli bir düzgün dairesel hareket tanımlar.
Formüller

r yarıçaplı bir dairede hareket için, dairenin çevresi C = 2π r’dir. Bir rotasyon için dönem T, aynı zamanda açısal sürat olarak bilinen rotasyonun açısal değeri, ise ω :
Ve birimler radyan/saniye’dir.
Daireyi dolaşan nesnenin hızı:
T sürede süpürülen θ açısı:
Yöndeki değişiklikten kaynaklanan ivme:
Vektörel ilişkiler Şekil 1’de gösteriliyor. Rotasyon ekseni ω = dθ / dt genliğiyle ve yörünge düzlemine dik Ω vektörü olarak gösterilmiştir. Ω vektörünün yönü sağ el kuralı kullanılarak seçilmiştir. Rotasyon belirlemek için olan bu kuralla, sürat vektör çarpı ürün olarak verilir; F burda vektör hem Ω hem de r ( t )’ye dikey, yörüngeye teğet ve ω r genliğindedir.
Aynı şekilde, ivme :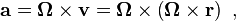 olarak verilir, burda vektör ω |v| = ω2 r genliğinde hem Ω hem de v ( t )’ye dikeydir ve r ( t )’nin tam zıddı yöne doğrultulmuştur.
olarak verilir, burda vektör ω |v| = ω2 r genliğinde hem Ω hem de v ( t )’ye dikeydir ve r ( t )’nin tam zıddı yöne doğrultulmuştur.
En basit olarak hız, kütle ve yarıçap sabittir.
Bir kilogramlık bir cismin saniyede bir radyanın açısal süratiyle bir metre yarıçap etrafında dairesel olarak hareket ettiğini varsayalım.
• Hız saniyede 1 metredir. • İçeriye doğru ivme 1 m / s2’dir. • 1 m / s2’de 1 kilogram merkezcil güce bağlıdır ve bu bir newton eder. • Cismin momentumu 1 kg•m•s−1’dir. • Eylemsizlik momentumu 1 kg•m2’dir. • Açısal momentumu 1 kg•m2•s−1’dir. • Kinetik enerji ½ jouledür. • Yörüngenin çevresi 2π (~ 6.283) metredir. • Hareketin devri dönüş başında 2π saniyedir. • Frekans (2π)−1 hertz’dir.
Kutupsal Koordinatlar
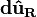 and
and 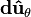 in the unit vectors
in the unit vectors 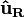 and
and 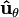 for a small increment
for a small increment 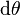 in angle
in angle 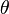 .
.Dairesel hareket boyunca cisim herhangi bir referans yönden konumlandırılmış θ (t) açısında orijin olarak alınan yörüngenin merkezinden R sabit uzaklığı olan kutupsal koordinat sistemi olarak tanımlanabilecek bir eğride hareket eder.
Bakınız Şekil 2. 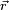 vektörünün yer değişimi orijinden parçacık konumuna olan radyal vektördür:
vektörünün yer değişimi orijinden parçacık konumuna olan radyal vektördür:
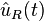 t süresinde orijinden uzaklaşan radyal vektöre paralel birim vektörün olduğu yerdir. Ortogonal birim vektörü
t süresinde orijinden uzaklaşan radyal vektöre paralel birim vektörün olduğu yerdir. Ortogonal birim vektörü 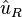 olarak da adlandırılan
olarak da adlandırılan 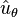 ’ye göstermek için uygun bir noktadır.
’ye göstermek için uygun bir noktadır. 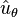 ’yi yörünge boyu dolaşım yönüne doğrultmak için müsaittir.
’yi yörünge boyu dolaşım yönüne doğrultmak için müsaittir.
Hız yerdeğişimin zamana göre türevidir:
Dairenin yarıçapı sabit olduğundan, hızın radyal bileşeni sıfırdır. 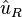 birim vektörü değişmez zamanlı birleşme genliğine sahiptir, böylece süre değiştikçe ucu daima
birim vektörü değişmez zamanlı birleşme genliğine sahiptir, böylece süre değiştikçe ucu daima 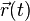 ile aynı açıda olan θ açısıyla birim yarıçapın dairesinde uzanır.
Eğer parçacık yerdeğişimi dt sürede dθ açısıyla dönerse dθ genliğindeki birim daire üzerinde bir yay tanımlayan
ile aynı açıda olan θ açısıyla birim yarıçapın dairesinde uzanır.
Eğer parçacık yerdeğişimi dt sürede dθ açısıyla dönerse dθ genliğindeki birim daire üzerinde bir yay tanımlayan 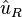 de döner.
de döner.
Bakınız Şekil 2’deki solda birim daire. Bu yüzden,
Değişimin yönü 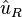 ’ye dikey (diğer bir değişle
’ye dikey (diğer bir değişle 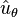 ) boyunca) olmalıdır çünkü
) boyunca) olmalıdır çünkü 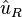 yönünde d
yönünde d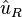 ’deki herhangi bir değişim
’deki herhangi bir değişim 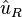 ’nin büyüklüğünü değiştirecektir.
’nin büyüklüğünü değiştirecektir.
İşaret pozitif çünkü dθ’daki artış nesne ve 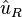 ’nin
’nin 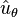 yönünde hareket ettiklerini gösteriyor.
yönünde hareket ettiklerini gösteriyor.
Bu yüzden hız,
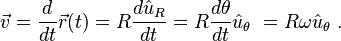 haline geliyor.
haline geliyor.
Cismin ivmesi de radyal ve teğet bileşenlere ayrılabilir. İvme, hızın zamana göre türevidir:
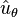 ’nin zamana göre türevi
’nin zamana göre türevi 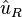 için olan aynı yöntemle bulunur.
Yine,
için olan aynı yöntemle bulunur.
Yine, 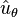 bir birim vektördür ve ucu π/2 + θ açılı bir birim daireyi takip eder. Dolayısıyla,
bir birim vektördür ve ucu π/2 + θ açılı bir birim daireyi takip eder. Dolayısıyla, 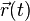 ile dθ açısındaki bir artış
ile dθ açısındaki bir artış 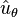 ’nin dθ genliğinde bir yayı izlediğini gösterir ve
’nin dθ genliğinde bir yayı izlediğini gösterir ve 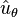
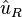 ’ye ortogontal olduğu için:
’ye ortogontal olduğu için:
Negatif işaret 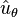 ’yi
’yi 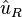 ’ye otogonal tutmak için zorunlu. (Aksi takdirde
’ye otogonal tutmak için zorunlu. (Aksi takdirde 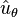 ve
ve 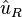 arasındaki açı dθ’daki artışla birlikte azalacaktı.)
Bakınız Şekil 2 solda birim daire. Sonuç olarak ivme:
arasındaki açı dθ’daki artışla birlikte azalacaktı.)
Bakınız Şekil 2 solda birim daire. Sonuç olarak ivme:
Merkezcil hızlanma yarıçap içine doğru yönlendirilen radyal bileşendir.
Teğet bileşen süratın genliğini değiştirirken:
Karmaşık sayıları kullanma
Dairesel hareket karmaşık sayılar kullanılarak tanımlanabilir. 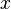 ekseni reel eksen ve
ekseni reel eksen ve 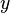 ekseni sanal eksen olsun. Cismin konumu bu durumda
ekseni sanal eksen olsun. Cismin konumu bu durumda 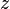 , karmaşık “vektör”, olarak verilebilir.
, karmaşık “vektör”, olarak verilebilir.
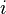 sanal birim ve
sanal birim ve
reel eksen ile karmaşık vektörün açısıdır ve t süresinin bir fonksiyonudur. Yarıçap sabit olduğundan:
Her bir nokta zaman farklılığını temsil eder. Bu formül ile sürat:
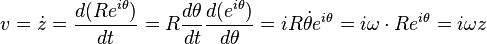 haline gelir.
haline gelir.
Ve ivme:
İlk terim yerdeğiştirme vektörüne ters yönde ve ikinci terim daha önceki sonuçlarda gösterildiği gibi dikeydir.
Sürat (.)(.)
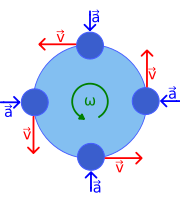
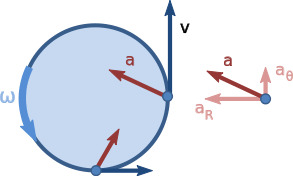
Şekil 1 sürat ve ivme vektörlerinin yörüngede dört farklı noktadaki değişmeyen hareketlerini gösteriyor. v vektörü dairesel yola teğet olduğu için, iki vektör hiçbir zaman aynı yöne doğrulmaz. Nesne sabit bir hıza sahip olmasına rağmen, yönü sürekli değişir. Sürattaki bu değişim genliği sabit tutulan (süratin olduğu gibi) fakat yönü sürekli değişen a ivmesinden kaynaklanır. İvme yarıçapın içine doğru (merkezcil olarak) yönelir ve sürate diktir. Bu ivme merkezcil ivme olarak bilinir
Bir r yarıçaplı yol için, bir θ açısı süpürüldüğünde yörünge çevresinde gidilen mesafe s = rθ’dır. Bu yüzden, yörünge etrafında dönüşün hızı:
Rotasyonun açısal değeri ω’dir. (Yeniden düzenleme ile, ω = v/r.) Yani, vdeğişmez ve sürat vektörü v de sabit genlik v ile aynı ω açısal değerinde döner.
Bağıl Dairesel Hareket
Bu durumda üç ivme vektörü üç sürat vektörüne diktir,
Ve bütün referans çerçevelerinde aynı skaler sabit olarak ifade edilen düzgün ivmenin karesine dik,
Dairesel hareketin ifadesi haline gelir.
Ya da pozitif karekökünü alarak ve üç ivmeyi kullanarak, dairesel hareket için uygun ivmeye ulaşırız:
İvme
Şekil 2’deki sol daire iki komşu zamanda sürat vektörlerini gösteren yörüngedir. Sağda, bu iki sürat kuyrukları çarpıştırılmak için hareket ettiriliyor. Hız sabit olduğu için, sağdaki sürat vektörler zaman geçtikçe bir daire oluşturuyor. Bir dθ = ω dt süpürülme açısı için, v’deki değişiklik v’nin sağ açılarında ve v dθ genliğinde bir vektördü, ki bu dolayısıyla ivme genliği şöyle verilmiştir:
Bazı sürat yarıçap ve genlik değerleri için merkezcil ivme
|v| r |
1 m/s 3.6 km/h 2.2 mph |
2 m/s 7.2 km/h 4.5 mph |
5 m/s 18 km/h 11 mph |
10 m/s 36 km/h 22 mph |
20 m/s 72 km/h 45 mph |
50 m/s 180 km/h 110 mph |
100 m/s 360 km/h 220 mph | |
|---|---|---|---|---|---|---|---|---|
| Slow walk | Bicycle | City car | Aerobatics | |||||
| 10 cm 3.9 in |
Laboratory centrifuge |
10 m/s² 1.0 g |
40 m/s² 4.1 g |
250 m/s² 25 g |
1.0 km/s² 100 g |
4.0 km/s² 410 g |
25 km/s² 2500 g |
100 km/s² 10000 g |
| 20 cm 7.9 in |
5.0 m/s² 0.51 g |
20 m/s² 2.0 g |
130 m/s² 13 g |
500 m/s² 51 g |
2.0 km/s² 200 g |
13 km/s² 1300 g |
50 km/s² 5100 g | |
| 50 cm 1.6 ft |
2.0 m/s² 0.20 g |
8.0 m/s² 0.82 g |
50 m/s² 5.1 g |
200 m/s² 20 g |
800 m/s² 82 g |
5.0 km/s² 510 g |
20 km/s² 2000 g | |
| 1 m 3.3 ft |
Playground carousel |
1.0 m/s² 0.10 g |
4.0 m/s² 0.41 g |
25 m/s² 2.5 g |
100 m/s² 10 g |
400 m/s² 41 g |
2.5 km/s² 250 g |
10 km/s² 1000 g |
| 2 m 6.6 ft |
500 mm/s² 0.051 g |
2.0 m/s² 0.20 g |
13 m/s² 1.3 g |
50 m/s² 5.1 g |
200 m/s² 20 g |
1.3 km/s² 130 g |
5.0 km/s² 510 g | |
| 5 m 16 ft |
200 mm/s² 0.020 g |
800 mm/s² 0.082 g |
5.0 m/s² 0.51 g |
20 m/s² 2.0 g |
80 m/s² 8.2 g |
500 m/s² 51 g |
2.0 km/s² 200 g | |
| 10 m 33 ft |
Roller-coaster vertical loop |
100 mm/s² 0.010 g |
400 mm/s² 0.041 g |
2.5 m/s² 0.25 g |
10 m/s² 1.0 g |
40 m/s² 4.1 g |
250 m/s² 25 g |
1.0 km/s² 100 g |
| 20 m 66 ft |
50 mm/s² 0.0051 g |
200 mm/s² 0.020 g |
1.3 m/s² 0.13 g |
5.0 m/s² 0.51 g |
20 m/s² 2 g |
130 m/s² 13 g |
500 m/s² 51 g | |
| 50 m 160 ft |
20 mm/s² 0.0020 g |
80 mm/s² 0.0082 g |
500 mm/s² 0.051 g |
2.0 m/s² 0.20 g |
8.0 m/s² 0.82 g |
50 m/s² 5.1 g |
200 m/s² 20 g | |
| 100 m 330 ft |
Freeway on-ramp |
10 mm/s² 0.0010 g |
40 mm/s² 0.0041 g |
250 mm/s² 0.025 g |
1.0 m/s² 0.10 g |
4.0 m/s² 0.41 g |
25 m/s² 2.5 g |
100 m/s² 10 g |
| 200 m 660 ft |
5.0 mm/s² 0.00051 g |
20 mm/s² 0.0020 g |
130 m/s² 0.013 g |
500 mm/s² 0.051 g |
2.0 m/s² 0.20 g |
13 m/s² 1.3 g |
50 m/s² 5.1 g | |
| 500 m 1600 ft |
2.0 mm/s² 0.00020 g |
8.0 mm/s² 0.00082 g |
50 mm/s² 0.0051 g |
200 mm/s² 0.020 g |
800 mm/s² 0.082 g |
5.0 m/s² 0.51 g |
20 m/s² 2.0 g | |
| 1 km 3300 ft |
High-speed railway |
1.0 mm/s² 0.00010 g |
4.0 mm/s² 0.00041 g |
25 mm/s² 0.0025 g |
100 mm/s² 0.010 g |
400 mm/s² 0.041 g |
2.5 m/s² 0.25 g |
10 m/s² 1.0 g |
Düzensiz Dairesel Hareket
Düzensiz dairesel hareket dairesel bir yolda hareket eden bir nesnenin sahip olduğu değişken bir hızın olduğu her durumdur. Teğetsel ivme sıfırdan farklıdır; hız değişkendir.
Sıfırdan farklı bir teğetsel ivme olduğu için, kendi merkezcil gücüne (kütle ve radyal ivmeden oluşan) ek olarak, bir nesne üzerine etki eden güçler vardır. Bu güçler ağırlık, normal kuvvet ve sürtünme kuvvetini içerir.
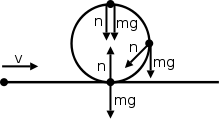
Düzensiz dairesel harekette, normal kuvvet her zaman ağırlığın tersi yöne doğrulmaz. İşte düz bir şekilde hareket eden ve aniden düz bir yola geri atlayan bir nesne görüyorsunuz. Bu diyagram ağırlığın tersi yönden ziyade farklı yönlere doğrulan normal kuvveti gösteriyor. Normal kuvvet aslında ağırlık kuvvetini önlemek ve merkezcil kuvvete katkı sağlamaya yardım eden radyal ve teğet kuvvetlerin toplamıdır. Merkezcil kuvvete katkı sağlayan Normal kuvvetin yatay bileşenidir. Normal kuvvetin dikey bileşeni ise nesnenin ağırlığına karşı koyar.
Düzensiz dairesel harekette normal kuvvet ve ağırlık aynı yöne doğru olabilir. İki kuvvet de aşağıya doğrulabilir fakat nesne aşağıya düşmeden dairesel bir yolda kalacaktır. Öncelikle normal kuvvetin neden ilk olarak aşağıya doğrulacağını görelim. İlk diyagramda, nesnenin bir uçağın içinde oturan bir insan olduğunu varsayalım, iki güç de yalnızca nesne dairenin tepesine ulaştığında aşağıya yöneliyor. Hem ağırlık hem de merkezcil kuvvet dairenin tepesindeyken aşağıya yöneldiğinden, normal kuvvet de aşağıya yönelecektir. Mantıklı bir açıdan, uçakta seyahat eden bir kişi dairenin tepe noktasında tepetaklak olacaktır. O anda, kişinin koltuğu aslında kişi üzerine bastırır ve bu normal kuvvettir
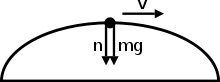
Nesnenin yalnızca aşağıya doğru olan kuvvetlere maruz kaldığında aşağıya düşmeme nedeni basittir. Bir nesneyi fırlatıldıktan sonra havada tutanın ne olduğunu bir düşünün. Bir nesne havaya atıldığı anda, nesne üzerine etki eden aşağıya doğru tek kuvvet yerçekimi kuvvetidir. Bu bir nesne havaya atıldığında hemen yere düşeceği anlamına gelmez. Nesneyi havada tutan şey süratidir. Newton’un hareket yasalarının ilki bir nesnenin eylemsizliği onu hareketli tuttuğunu belirtir ve nesne havadayken bir sürati olduğundan o yönde hareket etmeyi sürdürmeye eğilim gösterir.
Uygulamalar
Düzensiz dairesel hareket ile ilgili çözüm uygulamaları kuvvet analizlerini içerir. Düzgün dairesel hareketle, bir dairede hareket eden nesne üzerine etki eden tek kuvvet merkezcil kuvvettir. Düzensiz dairesel harekette, sıfırdan farklı bir teğetsel ivmeden dolayı nesne üzerine etkiyen ek kuvvetler vardır. Ek kuvvetler olmasına rağmen, nesne üzerine etki eden bütün kuvvetlerin toplamı merkezcil kuvvete eşit olmak zorundadır.
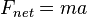
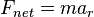
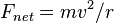
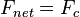
Radyal ivme total kuvvet hesaplanırken kullanılır. Teğetsel ivme nesneyi bir dairesel yolda tutmaktan sorumlu olmadığı için hesaplamada kullanılmaz. Nesneyi dairede hareket halinde tutan tek ivme radyal ivmedir. Bütün kuvvetlerin toplamı merkezcil kuvvet olduğu için, merkezcil kuvveti serbest cisim diyagramına çizmek gerekli değildir ve genellikle önerilmez.
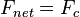 ’yı kullanarak, cisme etki eden ve
’yı kullanarak, cisme etki eden ve 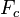 ’ye eşit kılan bütün kuvvetleri listelemek için serbest cisim diyagramları çizebiliriz. Daha sonra, bilinmeyenin ne olduğunu (bu bir kütle, sürat, eğrilme yarıçapı, sürtünme katsayısı, normal kuvvet vb. olabilir) çözebiliriz.
Örneğin yukarıdaki bir yarım dairenin tepe noktasındaki nesneyi gösteren görsel
’ye eşit kılan bütün kuvvetleri listelemek için serbest cisim diyagramları çizebiliriz. Daha sonra, bilinmeyenin ne olduğunu (bu bir kütle, sürat, eğrilme yarıçapı, sürtünme katsayısı, normal kuvvet vb. olabilir) çözebiliriz.
Örneğin yukarıdaki bir yarım dairenin tepe noktasındaki nesneyi gösteren görsel 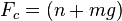 . olarak ifade edilebilir.
. olarak ifade edilebilir.
Düzgün dairesel harekette, dairesel yoldaki bir nesnenin total ivmesi radyal ivmeye eşittir. Düzensiz dairesel harekette teğetsel ivme var olduğundan, bu geçerli olmuyor. Düzensiz dairesel harekette bir nesnenin total ivmesini bulmak için, radyal ve teğetsel ivmenin toplam vektörünü bulun.
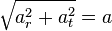
Radyal ivme yine 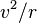 .’ye eşittir. Teğetsel ivme basit olarak verilen herhangi bir noktada süratin türevidir:
.’ye eşittir. Teğetsel ivme basit olarak verilen herhangi bir noktada süratin türevidir: 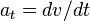 . Bu ayrı radyal ve teğetsel ivmelerin karelerinin toplamı kökü, yalnızca dairesel hareket için doğrudur; bu durumda radyal ivme
. Bu ayrı radyal ve teğetsel ivmelerin karelerinin toplamı kökü, yalnızca dairesel hareket için doğrudur; bu durumda radyal ivme 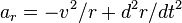 . olduğu için polar koordinatlarla
. olduğu için polar koordinatlarla 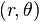 bir uçak içindeki genel hareket için Coriolis terimi
bir uçak içindeki genel hareket için Coriolis terimi 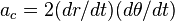
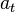 ’ye eklenmelidir.
’ye eklenmelidir.