Diffie-Hellman anahtar değişimi

Diffie-Hellman

Diffie-Hellman anahtar değişimi (D-H)^{[nb 1]}, kriptografik anahtarların değişiminde kullanılan özel bir yöntemdir. Bu kriptografi alanında uygulanan ilk pratik anahtar değişimi örneklerinden biridir. Diffie-Hellman anahtar değişimi metodu karşılıklı iki tarafın ortaklaşa güvensiz medya üzerinden ortak gizli anahtar elde etmelerine olanak sağlar. Bu anahtar daha sonra bir simetrik anahtar şifre kullanarak sonraki güvenli olmayan kanal'dan iletişim'i şifrelemek için kullanılabilir.

Bu tasarım ilk defa 1976 yılında Whitfield Diffie ve Martin Hellman tarafından "New Directions in Cryptography" isimli makalelerinde yayımlanmıştı. Her ne kadar bu tasarımı ayrı üzerinde çalışan ve yayımlamadan birkaç yıl önce İngiliz sinyalleri istihbarat teşkilatı, GCHQ kapsamında çalışan Malcolm J. Williamson tarafından da bulunmuş olmasına rağmen gizli tutulmuştu. 2002 yılında Hellman, açık-anahtarlı şifrelemenin icadında katkıda bulunan Ralph Merkle'e saygıdan bulmuş oldukları algoritmanın adını Diffie-Hellman-Merkle anahtar değişimi olarak adlandırılmasını önerdi (Hellman, 2002).

Diffie-Hellman anahtar anlaşması anonim (kimliği doğrulanmamış) anahtar-anlaşma protokolü olmasına rağmen, çeşitli kimliği doğrulanmış protokoller için temel oluşturur ve Taşıma Katmanı Güvenliği'nin (TLS) geçici modlarında kusursuz iletme gizliliği'ni sağlamak için kullanılır.

Yöntemi kısa bir süre sonra RSA takip etti, "asimetrik algoritmaları" kullanarak açık-anahtarlı şifreleme gerçekleştiriminde.

2002'de Martin Hellman:

Sistem...Diffie-Hellman anahtar değişimi olarak bilinmektedir. İlk defa sistem kağıt üzerinde Diffie ve benim tarafımdan açıklansa da, Merkle tarafından geliştirilmiş olan bir açık anahtar dağıtım sistemidir. Bundan dolayı 'Diffie-Hellman-Merkle anahtar değişimi' olarak adlandırılmalıdır. Ümit ediyorum bu küçük iletişim aracı Merkle'in açık anahtarlı kriptografi'nin icadına sağladığı katkıların tanınmasına yardımcı olur.

U.S. Patent 4,200,770 numara altında patentlenen bu sistemin patenti dolmuş olup, algoritmanın kendisini tanımlar ve mucidleri olarak Hellman, Diffie ve Merkle bilinir.^[1]

Tanım

Diffie-Hellman gizli iletişimlerde kullanılabilecek ortak gizli anahtar üretir. Bu anahtar da ortak ağlarda (güvenli olmayan kanaldan) güvenli veri alışverişini sağlar. Aşağıdaki diyagram anahtar değişiminin genel çalışma mantığını çok büyük sayılar yerine renkler kullanarak açıklar. Bu sürecin önemli bir parçası Alice ve Bob kendi gizli renklerini sadece karışım içinde değişirler. Sonunda her iki taraf matematiksel olarak arada dinleyen başka bir kişi tarafından geri döndürülmesi zor olan (bugünkü süper bilgisayarların mantıklı bir zamanda geri döndürememesi)aynı anahtarı elde eder. Bu aşamadan sonra Alice ve Bob oluşturmuş oldukarı ortak gizli anahtarla aralarındaki veri alışverişini şifrelemek ve deşifrelemek için kullanırlar. Sarı rengin zaten Alice ve Bob tarafından anlaştıklarına dikkat edin:

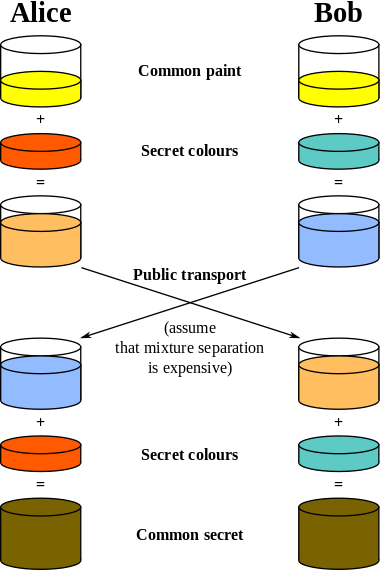
Şimdi ise bu şifrelemenin matematiksel olarak gerçekleştirimine açıklık getirelim:

Orijinal ve en sade haliyle protokolün gerçekleştirimi tamsayıların çarpımsal grubu modül p, burdaki p asal sayı ve g primitif kök mod p'ye göre. Aşağıda protokolle ilgili bir örnek verilmiştir. Gizli olmayan değerler mavi, gizli değerler ise kalın kırmızı ile gösterilmiştir:

Alice Bob Gizli Açık Hesaplar Gönderir Hesaplar Açık Gizli a p, g p,g${\displaystyle \rightarrow }$ b a p, g, A g^a mod p = A A${\displaystyle \rightarrow }$ p, g b a p, g, A ${\displaystyle \leftarrow }$ B g^b mod p = B p, g, A, B b a, s p, g, A, B B^a mod p = s A^b mod p = s p, g, A, B b, s

1. Alice ve Bob aralarında asal sayı olarak p=23 ve taban olarak g=5'i seçmeyi anlaşırlar.
2. Alice gizli bir tamsayı seçer a=6, ve Bob'a A = g^a mod p hesaplayıp gönderir.
   • A = 5⁶ mod 23
   • A = 15,625 mod 23
   • A = 8
3. Bob da gizli bir tamsayı seçer b=15, ve aynı şekilde Alice B = g^b mod p hesaplayıp gönderir.
   • B = 5¹⁵ mod 23
   • B = 30,517,578,125 mod 23
   • B = 19
4. Alice s = B ^a mod p yi hesaplar.
   • s = 19⁶ mod 23
   • s = 47,045,881 mod 23
   • s = 2
5. Bob da s = A ^b mod p yi hesaplar.
   • s = 8¹⁵ mod 23
   • s = 35,184,372,088,832 mod 23
   • s = 2
6. Bu aşamada Alice ve Bob aynı gizli anahtara sahiptirler: s = 2. Çünkü 6*15 ile 15*6 aynıdır. Bu yüzden bu iki gizli tamsayıyı bilen biri de s yi aşağıdaki gibi hesaplayabilir:
   • s = 5^6*15 mod 23
   • s = 5^15*6 mod 23
   • s = 5⁹⁰ mod 23
   • s = 807,793,566,946,316,088,741,610,050,849,573,099,185,363,389,551,639,556,884,765,625 mod 23
   • s = 2

Alice de Bob da aynı sonucu ulaştılar, çünkü (g^a)^b ve (g^b)^a ikisi de aynı mod p'ye göre. Dikkat ederseniz sadece a, b ve g^ab = g^ba mod p gizli tutulmuştu. Geri kalan bütün değerler – p, g, g^a mod p, and g^b mod p – açıkça gönderilmişti (hesaplanarak). Bir kere Alice ve Bob sadece kendilerinin bildiği ortak gizli anahtarı oluşturduktan sonra, bunu açık iletişim kanalında mesaj gönderimlerinde şifreleme anahtarı olarak kullanabilirler. Tabii ki, bu örneğimizi daha güvenli hale getirmek için daha büyük a, b, ve p değerlerine ihtiyacımız var, çünkü g^ab mod 23 bütün olası değerlerini denemek oldukça basit. Burada olası 23 tane tamsayı değeri vardır mod 23'ün sonucunda. Eğer p en az 300 haneli asal sayı olsaydı, ve a and b en az 100 haneli olsalardı, işte o zaman günümüzde bilinen en iyi algoritmalar bile sadece g, p, g^b mod p ve g^a mod p verilmiş bile olsa a yı bulamazlar, hatta insanoğlunun bütün işlem gücü verilse de. Bu ayrık logaritma problemi olarak bilinir. Dikkat edin g'nin büyük olmasına gerek yoktur, ve pratikte genelde 2, 3 veya 5 kullanılır.

Protokol hakkında daha genel bir açıklama:

1. Alice ve Bob sınırlı bir devirsel grup olan G ve Gde bulunan üretici eleman g de anlaşırlar. (Bu işlem genellikle protokolün geri kalan kısmından daha önce yapılır; g nin saldırganlar tarafından bilindiğini varsayıyoruz.) Grup G yi çarpımsal olarak yazacağız.
2. Alice rastgele bir a doğal sayısı seçer ve g^a yı Bob'a gönderir.
3. Bob da rastgele bir b doğal sayısı seçer ve aynı şekilde g^b yi hesaplayıp Alice gönderir.
4. Alice (g^b)^a hesaplar.
5. Bob da (g^a)^b hesaplar.

Şu aşamada Alice de and Bob da ortak gizli anahtar olarak kullanılabilecek g^ab ye sahipler. (g^b)^a ve (g^a)^b değerleri aynıdır çünkü gruplara kuvvet birleşimi uygulanabilir. (Ayrıca bakınız: Üslü sayı.)

mg^ab olarak gönderilen şifreli m metnini çözbilmek için, Bob (ya da Alice) ilk önce (g^ab)^-1 aşağıdaki gibi hesaplamalı:

Bob |G|, b, ve g^a yı biliyor. Grup teoriden G yapısına göre sonuç saptanır, x^|G| = 1 G de bulunan tüm x ler için.

Bob daha sonra (g^a)^|G|-b = g^a(|G|-b) = g^a|G|-ab = g^a|G|g^-ab = (g^|G|)^ag^-ab=1^ag^-ab=g^-ab=(g^ab)^-1 hesaplar.

Alice Bob'a, mg^ab şeklinde şifreli mesaj gönderdiğinde, Bob orijinal metni elde edebilmek için (g^ab)^-1 uygular ve orijinal metni mg^ab(g^ab)^-1 = m(1) = m geri döndürmüş olur.

Tablo

Bu tablonun amacı kimin hangi bilgilere sahip olduğunu kolayca anlaşılması içindir. (Eve Eavesdropper— Alice ve Bob'un arasındaki iletişimi içeriğini değiştirmeden dinliyor.)

• s = ortak gizli anahtar olsun. s = 2
• g = herkes tarafından bilinen taban(base) olsun. g = 5
• p = herkes tarafından bilinen (asal) sayı olsun. p = 23
• a = Alice'in gizli anahtarı olsun. a = 6
• A = Alice'in açık anahtarı olsun. A = g^a mod p = 8
• b = Bob'un gizli anahtarı olsun. b = 15
• B = Bob'un açık anahtarı olsun. B = g^b mod p = 19

Alice biliyor bilmiyor p = 23 b = ? base g = 5 a = 6 A = 5^6 mod 23 = 8 B = 5^b mod 23 = 19 s = 19^6 mod 23 = 2 s = 8^b mod 23 = 2 s = 19^6 mod 23 = 8^b mod 23 s = 2

Bob biliyor bilmiyor p = 23 a = ? base g = 5 b = 15 B = 5^15 mod 23 = 19 A = 5^a mod 23 = 8 s = 8^15 mod 23 = 2 s = 19^a mod 23 = 2 s = 8^15 mod 23 = 19^a mod 23 s = 2

Eve biliyor bilmiyor p = 23 a = ? base g = 5 b = ? s = ? A = 5^a mod 23 = 8 B = 5^b mod 23 = 19 s = 19^a mod 23 s = 8^b mod 23 s = 19^a mod 23 = 8^b mod 23

Not: Alice için Bob'un gizli anahtarını çözmek zor olmalı ya da Bob için Alice'in gizli anahtarını çözmek zor olmalı. Eğer, Alice için Bob'un gizli anahtarını çözmek (ya da tam tersi) zor olmazsa, Eve basitçe kendi gizli / açık anahtar çiftiyle değiştirebilir, ve Bob'un açık anahtarını kendi gizli anahtarına katıp, sahte ortak gizli anahtar oluşturur, ve Bob'un gizli anahtarını elde eder (elde edeceği anahtarla da ortak gizli anahtarı bulabilir. Bob'un gizli anahtarını bulabilmek için Eve gizli / açık anahtar çiftini hesaplamasını kolaylaştıracak şekilde seçmeyi deneyebilir). Diffie-Hellman pratikte demo'su için (pratiklik açısından küçük sayılar kullanın) ^[2].

Notlar

1. Synonyms of Diffie–Hellman key exchange include:
   • Diffie–Hellman key agreement
   • Diffie–Hellman key establishment
   • Diffie–Hellman key negotiation
   • Exponential key exchange
   • Diffie–Hellman protocol
   • Diffie;Hellman handshake

Kaynakça

1. "Cryptographic apparatus and method patent". google. http://www.google.com/patents?vid=4200770. Erişim tarihi: 5 Mayıs 2013. 
2. Diffie-Hellman Example

Örnekler

• Blum-Goldwasser Kriptosistem
• RSA
• Merkle-Hellman Kriptosistem