EPR paradoksu

Albert Einstein

EPR paradoksu (EPR özçelişkisi) kuantum (nicem) mekaniğinin Kopenhag yorumuna karşı erken ve etkili bir eleştiridir. Albert Einstein ve arkadaşları Boris Podolsky ve Nathan Rosen (topluca EPR olarak bilinen) kuantum mekaniğinin daha önce fark edilmemiş fakat belli sonuçlara sahip olan kabul edilmiş denklemlendirimini meydana çıkaran bir düşünce deneyi hazırladılar, ancak zamanla bu denklemlendirimler mantıksız göründü. Açıklanan senaryo kuantum dolaşıklığı olarak bilinen bir olay içeriyordu.

Kuantum mekaniğine göre, bazı koşullar altında, ortaklaşa veya bireysel olan çift kuantum sistemleri, çift sistemde gerçekleşen deneylerin sonuçlarının olasılıklarını kodlayan tek bir dalganın işleviyle tarif edilebilir. Aşağıda ele alınan EPR makalesi yazıldığında, yapılan deneyler sonucu, bir deneyin sonucunun bazen tek bir tahmini olmadığı biliniyordu. Bu tip bir belirsizlik, bir ışık süzmesi yarım gümüşlenmiş bir aynanın üzerine düştüğünde görülebilir. Işık süzmesinin yarısı yansırken diğer yarısı geçecektir. Eğer ışık süzmesinin şiddeti, tek bir foton geçene kadar indirgenirse, kuantum mekaniğinde fotonun yansıması veya geçişi tahmin edilemez.

Bu etkinin rutin açıklaması o zamanlar Heisenberg'in belirsizlik ilkesiyle sağlanmıştı. Fiziksel nicelikler eşlenik denilen çiftler halinde gelir. Bu tür eşlenik çiftlerinin örnekleri arasında konumu ve farklı eksenler etrafında ölçülen bir parçacığın ve bileşenlerinin devinirliği verilebilir. Bir nicelik ölçüldüğünde ve belirlendiğinde, birleşmiş nicelikler belirsizleşir. Heisenberg bunu ölçümden kaynaklanan bir rahatsızlık olarak açıklamıştır.

1935 yılında yazılmış bir EPR kağıdı, bu açıklamanın yetersiz olduğunu göstermeyi amaçlamıştır. A ve B olarak adlandırılan iki dolaşık parçacığı dikkate aldığımızda; A parçacığının miktarının ölçülmesi, B parçacığının eşleniğinin miktarının hiçbir temas ve karışıklık olmadan belirsizleşmesine neden olur.Temel fikir, bir sistemin içindeki iki parçacığın kuantum durumları, her zaman ikisinin ortak durumundan ayrışamaz. Bunun bra-ket yazılımındaki bir örneği şu şekildedir;

${\displaystyle |\Phi ^{+}\rangle ={\frac {1}{\sqrt {2}}}\left(|00\rangle +|11\rangle \right)}$

Heisenberg'in ilkesi bazen yerel olmayan denilen bir kuantum etkisinin klasik bir açıklamasının sağlanmasına çabaladı. EPR'ye göre bu durumun iki olası açıklaması vardı. Parçacıklar arasında ayrım olsa bile ya aralarında bir etkileşim vardı ya da tüm olası ölçümlerin sonuçları hakkında bilgiler parçacıklarda mevcuttu.

EPR yazarları ikinci açıklamayı, bazı kodlanmış 'gizli değişkenlerden' dolayı tercih etmişlerdir. Bir etki anında bir mesafe boyunca yayılan ilk açıklama, görelilik teorisi ile çelişmekteydi. Daha sonra, kuantum mekaniğinin kuralcılığından dolayı tamamlanmamış olduğu sonucuna vardılar çünkü bu tip gizli değişkenlere kuantum mekaniğinde yer yoktur.

Bell'in teorem sonuçlarındaki ihlaller genellikle Einstein, Poldolsky ve Rosen tarafından da varsayılan Bell'in teoreminin hipotezlerinin bizim dünyamızda geçerli olmamasından anlaşılmaktadır. Konuyu ve konuyla ilgili deneyleri inceleyen Alain Aspect ve grubu gibi fizikçilerin çoğu, EPR ilk dikkat çektiğinde, kuantum teorisinin öngördüğü gibi, EPR'in tercih ettiği “yerel gizli değişken” teorisini Bell eşitsizliklerini ihlal ettiğinden ötürü geçersiz kabul etti.

EPR gelişimlerinin tarihi

Bu konuları ilk ortaya koyan makale, 1935 yılında yayınlanan "Fiziksel Gerçekliğin Kuantum Mekaniksel Tanımı Tam Olarak Düşünülebilir Mi?"'dir. Einstein kuantum mekanik biçimciliği açısından ölçümlerle yorumlanarak ortaya çıkanlar dışındaki nesnel fiziksel bir gerçekliğin var olduğu görüşünü protesto etmiş, kendi düşüncesine daha çok uyan nedensellik teorisi için hayatının sonuna kadar mücadele etmiştir. Ancak, Einstein'ın ölümünden sonra, bir EPR kağıdında anlatılan andıran deneyler Fransız bilim adamları Lamehi-Rachti ve Mittig tarafından 1976 yılında Saclay Nükleer Araştırma Merkezinde gerçekleştirilmiştir. Bu deneyler, yerel gerçekçilik fikrinin yanlış olduğunu göstermiştir.

Kuantum mekaniği ve yorumlanması

Yirminci yüzyılın başından beri, kuantum kuramı, doğru mezoskopik ve mikroskobik dünyanın fiziksel gerçekliğini açıklayan birden fazla tekrarlanabilir fizik deneylerinde başarılı olduğunu kanıtlamıştır.

Kuantum mekaniği, atomunları tanımlayan ve bir ölçüm cihazında gözlenen tayfi çizgileri açıklama amacı ile geliştirilmiştir.Yirminci yüzyılın başlarında iddialı olmasına rağmen, konuyla ilgili henüz ciddi bir meydan okuma yapılmamıştır. Kuantum olaylarının felsefi yorumlaması, ancak, başka bir meseledir: kuantum mekaniğinin matematiksel denklemlendirimini yorumlamanın nasıl olacağının sorusu farklı felsefi görüşlerden insanların farklı cevaplar vermesini doğurmuştur.

Kuantum teorisi ve kuantum mekaniği belirleyici bir şekilde tek ölçüm sonuçları vermemektedir. Kopenhag yorumlaması olarak bilinen kuantum mekaniği anlayışına göre, ölçümlerin dalga işlevlerinin anlık çökmesine neden olması, özdurumdaki kuantum sistemini betimler. Einstein, 1927 Solvay Konferansında bu çökmenin canlandırmasını yapmıştır. Deneyi, iç yüzeyi algılanım ekranına sahip küredeki küçük bir delikten elektron tanımlamasıyla yapmıştır. Bu deneyde elektronlar kürenin iç yüzeyiyle yaygın olarak dağınık bir şekilde temasta bulunmuştur. Ancak bu elektronlar dalga cephelerinin girdiği noktadan bütün yönlere genişlemesiyle açıklanabilir. Günlük yaşamdan da anlaşılacağı gibi bir dalga algılanım ekranında geniş bir bölge kaplar fakat elektronların tek noktalarda ekrana bir etkisi olacaktır ve sonunda kendi özdeş dalga fonksiyonları tarafından açıklanan olasılıkları doğrultusunda bir model oluşturacaktır. Einstein, konumuna bağlı olarak neden her elektronun dalgasının ön cephesinin çöktüğünü, niye elektronların yüzey üzerindeki enerji gibi loş olması yerine tek parlak pırıldanımlar olarak görünmesini ve neden tek bir elektronun herhangi bir nokta yerine sabit tek bir noktada bulunduğunu sorar. Elektronların davranışı, bütün olası noktalara gönderilmiş fakat biri dışında tüm hepsini geçersiz kılan bazı sinyallerin izlenimini verir. Diğer bir değişle, tüm noktalar haricinde tek bir nokta seçilebilir.

Einstein'ın karşıtlığı

Einstein Kopenhag yorumunun en önemli rakibi oldu. Onun görüşüne göre, kuantum mekaniği tamamlanmamıştı. Bunu yorumlayan, John von Neumann ve David Bohm gibi diğer yazarlar orijinal kağıt açıkca iddia edilmemiş, rastgele yapılan ölçüm sonuçlarından 'gizli' değişkenleri sorumlu tutmuştur.

1935 EPR kağıdı felsefi tartışmayı fiziksel bir tartışmanın içine sıkıştırmıştır. Yazarlar bir ölçümün sonucu olan verilmiş özgül bir deneyde ölçüm gerçekleşmeden önce gerçeklik unsuru denilen bir şeyin gerçek dünyada var olduğunu iddia etmişlerdir. Yazarlar, gerçekliğin bu unsurlarının her uzayzamandaki belli bir noktaya ait olduğunu yani yerel olduğunu varsaymaktadır. Her element sadece uzay-zamanın (yani, geçmişin) onun ışık konisinin gerisinde bulunan olaylardan etkilenmiştir. Bu iddialar artık yerel gerçekçilik olarak bilinen teşkil doğası hakkında varsayımlar üzerine kurulmuştur.

EPR kağıdı sık sık Einstein'ın görüşlerinin tam bir ifadesi olarak alınmış olsa da, başta Einstein ve Rosen ile Gelişmiş Çalışma Enstitüsündeki görüşmelere dayanarak, Podolsky tarafından yazılmıştır. Einstein, daha sonra Erwin Schrödinger'e "bu, benim normalde istediğim gibi bir sonuç vermedi, daha ziyade, önemli şey, tabiri caizse, biçimcilik tarafından boğuldu." demiştir. 1936 yılında, Einstein yerel gerçekçi fikirlerinin bir bireysel hesabını sundu.

Paradoksun tanımı

Orijinal EPR paradoksu, kuantum mekaniğinin bir tahmini olan bir kuantum parçacığının konumunun ve devinirliğinin aynı anda bilinememesine meydan okur. Bu meydan okuma, başka fiziksel özelliklerin diğer çiftlerinin genişlemesiyle olabilir.

EPR kağıdı

Orijinal kağıt, etkileşime geçmesine izin verilen iki sisteme ne olacağını ve bir süre sonra etkileşim kalmadığında neler olacağını tanımlama amacı gütmüştür. Kumar'ın sözleriyle bu, A ve B olan iki parçacığın kısaca etkileşimde olması ve daha sonra farklı yönlere hareket etmesi olarak tanımlanabilir. Heisenberg'in belirsizlik ilkesine göre, devinirliği ve B parçacığının tam olarak konumunu aynı anda ölçmek mümkün değildir fakat Kumar'a göre A parçacığının kesin konumunu belirlemek mümkündür. Bu nedenle, ölçümler sonucu A'nın bilinen kesin konumu yardımıyla B'nin kesin konumu bulunabilir. Ayrıca, A parçacığının devinirliği ölçülebildiğinden, B parçacığınınkini de A'ya bağlı olarak bulmak mümkündür. Kumar, bunu şu şekilde yazmıştır; “EPR, B parçacığı eş zamanlı olarak kesin ve gerçek bir devinirlik ve konum değerine sahiptir yargısını kanıtlamış ve savunmuştur.” EPR, B parçacığı fiziksel olarak rahatsız olma olasılığı olmadan, parçacık A üzerinde yapılan ölçümler sonucunda B'nin ya devinirliğinin ya da pozisyonunun kesin değerlerini bulmayı amaçladı.

EPR Kuantum Mekaniği gerçek uygulama aralığını sorgulamak için bir paradoks yaratmaya çalıştı. Bu paradoks; Kuantum teorisi iki değerin de parçacık için tahmin edilemez olmasını ve henüz EPR düşünce deneyinin hepsinin belirli değerlere sahip olması gerektiğini göstermesini içeriyordu. EPR kağıdı: "Biz, fiziksel gerçekliğin kuantum mekaniksel tanımının tam olarak dalga işlevleri tarafından açıklanamayacağı sonunu kabul etmek zorunda kalıyoruz.” demiştir.

EPR kağıdı şu söz ile sonlanır: Biz böylece dalga fonksiyonun fiziksel gerçekliğin tam bir açıklamasını yapamadığını göstersek de, biz böyle bir açıklamanın var olup olmadığı sorusuna kesin bir cevap bulamadık. Biz böyle bir teori mümkün olduğuna, yine de, inanıyoruz.

Dolaşık durumda ölçümler

Elimizde elektron-pozitron çiftlerini yayan bir kaynak var ve Alice adından bir gözlemcinin olduğu A noktasına elektron, Bob adında bir gözlemci bulunan B noktasına da pozitron gönderiyoruz. Kuantum mekaniğine göre, kaynağımızı, yayılan her çiftin tekli fırıl adı verilen kuantum durumunu işgal edeceği şekilde ayarlayabiliriz. Böylece, bu parçacıklar dolaşıktır diyebiliriz. Bu, durum 1 ve durum 2 olarak adlandırdığımız iki kuantum çakışması durumu olarak görülebilir. Durum 1de, pozitif z ekseninde bir fırılı olan elektron ve negatif z ekseninde bir fırıla sahip pozitron vardır. Durum 2de ise, elektron negatif z ekseninde bir fırıla sahipken, pozitif z ekseninde pozitron bir fırıla sahiptir. Bundan dolayı, ölçüm yapmadan tekli fırıl durumundaki bir parçacığın durum fırılını belirlemek mümkün değildir.

Elektron-pozitron çiftiyle yapılan EPR düşünce deneyi. Merkezdeki kaynak iki gözlemciye parçacık gönderir; sol taraftaki Alice gözlemcisine elektron gönderirken, sağ taraftaki Bob gözlemcisine pozitron gönderilir ve fırıl ölçümleri yapılabilir.

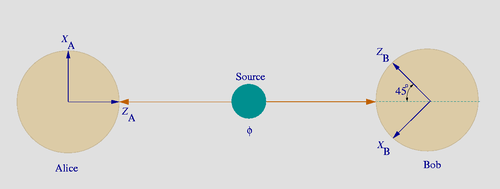
Artık, Alice z ekseni etrafındaki fırılı ölçer ve +z veya -z olmak üzere iki muhtemel sonuç elde edebilir. Eğer elde ettiği sonuç +z ise; kuantum mekaniğinin Kopenhag yorumlamasına göre sistemin kuantum durumu durum 1de çöker. Kuantum durumu sistemde gerçekleşen her türlü ölçümün sonucunu belirler. Bu durumda, eğer Bob z ekseni etrafında sonradan ölçüm yaparsa, bulacağı sonuç -z ekseninde olur. Aynı şekilde, eğer Alice -z ekseninde sonuç alırsa, Bob +z ekseninde bir sonuç alır.

Özellikle z eksenini seçmemizin belirli bir nedeni yoktur, kuantum mekaniğine göre tekli fırıl durumu x eksenini gösteren fırıl durumunun çakışması da eşit olur. Eğer Alice ve Bob fırılı x ekseninde ölçmeye karar verirse, buna durum 1a ve durum 2a deriz. Durum 1a'da, Alice'in elektronu +x fırılına sahipken, Bob'un pozitronu -x fırılına sahiptir. Durum 2a'da ise, Alice'in elektronu -x fırılına sahipken, Bob'un pozitronu +x fırılına sahiptir. Bundan dolayı, Eğer Alice +x ölçerse, sistem durum 1ada çöker ve Bob -x sonucunu elde eder. Eğer Alice -x ölçerse, sistem durum 2a'da çöker ve Bob +x sonucunu elde eder.

Herhangi bir eksende fırılları ölçülürse, sonuç her zaman birbirlerinin tersi olur. Bu durum, sadece parçacıklar birbirlerine bağlıysa açıklanabilir. Ya her eksende kesin olarak farklı fırıla sahip şekilde yaratılmışlardır (gizli değişken tartışması) ya da birbirlerine bağlılardır ve bu yüzden bir elektron diğerinin eksenin hangi tarafında olduğunu hissediyordur ve onun karşıt sonucunu alıyorudur (dolaşıklık tartışması). Ayrıca, eğer iki parçacığın farklı eksenler boyunca fırılları ölçülüyorsa, x ekseninde elektron fırılı ölçüldüğünde (ve x eksenindeki pozitronun fırılı yok sayıldığında), z eksenindeki pozitronun fırılı kesin değildir çünkü ölçüm yerini almıştır ve zaten ikinci bir eksende fırılı mevcuttur. Buna rağmen, deneyler tarafından onaylanan kuantum mekaniği hakkındaki varsayımlar, herhangi bir gizli değişken teorisiyle açıklanamaz. Bu, Bell teoreminde gösterilmiştir.

Kuantum mekaniğinde,Heisenberg belirsizlik ilkesine göre iki değişken için de kuantum durumu kesin bir sonuca sahip olamaz ve bu durum x-fırılı ve z-fırılı “uyumsuz gözlemlenenlerdir” anlamına gelir. Alice'in z-fırılı ölçtüğünü varsayalım ve bulduğu sonuç +z olsun, bu durumda kuantum durumu durum 1de çöker. Şimdi, z-fırılını ölçmek yerine, Bob x-fırılını ölçsün. Kuantum mekaniğine göre, eğer sistem durum 1de ise, Bob'un x-fırıl ölçümü %50 ihtimalle +xde olabilir ya da %50 ihtimalle -xde olabilir. Bob'un kendisi ölçüm yapana kadar, nasıl bir sonuç elde edileceğini tahmin etmek imkansızdır.

Bu, konunun dönüm noktasıdır. Bob pozitronun x-fırılını ölçtüğünde, kesin bir sonuca ulaşabilir çünkü kendi parçacığını rahatsız etmemiştir. Bob'un pozitronu %50 ihtimalle +x veya -x'dedir ve kesin bir sonuç yoktur çünkü Bob'un pozitronu Alice'in elektronunu bilir ve Alice'in elektronu bilinip ölçüldüğü için Bob'un elektronunun spini hakkında kesin bir bilgi elde edemeyiz.

Kopenhag yorumuna göre, dalga işlevi ölçüm yapıldığı zaman çöker ve bu yüzden belli bir uzaklıkta bir etki olmalıdır veya pozitron bilmesi gerekenden daha fazlasını bilmelidir.

Paradoksun özeti

İlk parçacığın fiziksel ölçümleri kendi konumunda devinirliğe etkisi kesin değildir fakat ilk parçacığın devinirliğini ölçmek öbürünün konumunun kesinliğini etkiler. Einstein, Podolsky ve Rosen, ikinci parçacığın nasıl kesin olmayan konumuna rağmen kesin bir devinirliğe sahip olduğunu sorguladı. Bir parçacık diğeriyle uzayda iletişim halinde olduğundan, bu bir “paradokstur”.

Bu arada, Bell, fırılı kendi örneğinde kullandı fakat kuantum mekaniğinde gözlemlenebilirler denilen birçok çeşit fiziksel nicelik kullanılıyordu. EPR kağıdı, bu gözlemlenebilirlerin devinirliği için kullanılıyordu. EPR planının deneysel gerçekleştirmeleri genellikle foton kutuplaşmasında kullanıyor çünkü kutuplaşmış fotonların hazırlanması ve ölçülmesi kolaydır.

EPR deneylerindeki yerellik

Yerellik ilkesi, bir yerde meydana gelen fiziksel işlemlerin başka bir yerdeki gerçeklik unsurları üzerinde bir etkisinin olmaması gerektiğini belirtir. İlk bakışta, bu bilgiler nedenselliği ihlal etmeden ışık hızından daha hızlı iletilmeyen bilgileri savunan özel göreliliğin sonuçları hakkında makul bir varsayım gibi görünüyordu. Genellikle nedenselliği ihlal eden herhangi bir teori de içten tutarsız olacağından, yararsız olacağı düşünülmektedir.

Kuantum mekaniği ve klasik tanımların birleştirmek için olan olağan kurallar, nedensellik yasasını ihlal etmeden yerellik ilkesini ihlal etmektedir. Nedensellik korunmaktadır çünkü Alice'in Bob'un ölçüm eksenini yönlendirerek mesaj iletmesinin başka bir yolu yoktur. Alice hangi ekseni kullanırsa kullansın, %50 oranında + veya – sonuç elde etme olasılığı vardır ve kuantum mekaniğine göre temel olarak hangi sonucu alacağını etkilemesi imkansızdır. Ayrıca, Bob sadece bir kez kendi ölçümünü yapabilir çünkü kuantum mekaniğinin temel özelliği aldığı elektronların milyon tane kopyasını yapmasını, hepsine tek tek fırıl ölçümü yapmasını ve sonuçların istatiksel dağılımına bakmasını imkansız kılar. Bu nedenle, eğer sadece bir ölçüm yapmasına izin verilirse, + veya – sonuç bulması Alice'le aynı eksende olup olmamasına bağlı olmadan %50 şansı olduğunu görürüz.

Yine de, yerellik ilkesi fiziksel sezgilere güçlü bir şekilde hitap etmiştir ve Einstein, Podolsky ve Rosen bu yüzden bu teoriyi terk etmek istemiyorlardı. Einstein, kuantum mekaniksel tahminlerle “bir noktada ürkütücü” diyerek dalga geçmiştir. Bu nedenle, kuantum mekaniğinin henüz tamamlanmamış olmasıyla sonuçlandırmışlardır.

Son yıllarda ise, EPR'nin ulaştığı sonuç yerellik anlamadaki gelişmelerden ve kuantumun elverişli olmamasından şüphe uyandırmıştır. Yerellik kelimesi, fizikte birçok anlama sahiptir. Örneğin, kuantum alan teorisinde "yerellik" uzayın değişik noktalarındaki kuantum alanlarının birbirleriyle etkileşimde olmamaları anlamına gelir. Ancak, bu anlamda "yerel" olan kuantum alan teorileri EPR tarafından tanımlanan yerellik ilkesine aykırı görünmektedir, ama yine de daha genel anlamda yerelliği ihlal etmezler. Dalga işlevinin çöküşü, kuantum elverişsizliğinin epifenomeni olarak görülebilir. Temel davranış yerel nedenselliği ihlal etmediğinden, bu gerçek ya da belirgin olsun, dalga fonksiyonu çöküşü ek bir etki yapar. Yukarıdaki örnekte belirtilen nedenle, ne EPR deneyinim ne de herhangi bir kuantum deneyinin gösterilmesinin ışık sinyalinden hızlı olması mümkün değildir.

Paradoksun çözümü

Gizli değişkenler

EPR paradoksunu çözmek için çeşitli yollar vardır. EPR tarafından önerilen bir tanesi, kuantum mekaniğidir, deneysel senaryolarda çeşitli başarılar elde etmesine rağmen, aslında tamamlanmamış bir teoridir. Diğer bir deyişle, kuantum mekaniği (bir derece başarılı bir de olsa) istatistiksel yaklaşım gibi davranan doğanın henüz keşfedilmemiş bazı teorileri vardır. Kuantum mekaniğinin aksine, daha tam bir teori tüm "gerçeklik unsurlarına" karşılık gelen değişkenleri içerebilir. Heisenberg belirsizlik ilkesi, yani "iletmez kuantum gözlenebilirlerinin" gözlenen etkilerine yol vermek için bu değişkenler üzerinde hareket eden bazı bilinmeyen mekanizmalar olmalıdır. Böyle bir teoriye gizli değişken teorisi denir.

Bu fikir göstermek için, yukarıdaki düşünce deneyi için çok basit bir gizli değişken teorisini hazırlayabiliriz. Bir kaynaktan yayılan kuantum tekli-fırıl durumu doğru fiziksel durum için x-fırılı ve z-fırılının kesin değeri için yaklaşık bir tanım oluşturur. Bu "gerçek" durumlarda, Bob'a giden pozitron her zaman Alice'e giden elektronun ters fırıl değerine sahip olacaktır, ancak aksi bir durumda değerler tamamen rastgele olacaktır. Örneğin, kaynak tarafından yayılan ilk çift "Alice'e (+z,-x) ve Bob'a (-z, +x)" olabilir, bir sonraki çift ise "Alice'e (-z,-x) ve Bob'a (+z, +x) "ve benzerleri olabilir. Bu nedenle, Bob'un ölçme ekseni, Alice'inki ile aynı hizada ise, Bob mutlaka Alice ne gelirse tersini alacak; aksi halde, Bob eşit olasılıkla "+" veya "-" alıcaktır.

Ölçümlerimizi z ve x eksenleriyle sınırladığımızı varsayarsak, böyle bir gizli değişken teorisi kuantum mekaniğinden deneysel olarak ayırt edilemez. Gerçekte, Alice ve Bob'un kendi ölçümlerini yaptığı sonsuz sayıda eksen olabilir, bu yüzden sonsuz sayıda bağımsız gizli değişkenler olması gerekir. Ancak, bu ciddi bir sorun değildir çünkü biz gizli değişken teorisini çok basit bir şekilde bağıntısal yazdık ve daha sofistike bir teorinin bu konuda yama yapması mümkün olabilir. Bu gizli değişkenlerin fikrinde çok daha ciddi bir sorun olduğunu ortaya çıkıyor.

Bell eşitsizlikleri

1964 yılında, John Bell, EPR düşünce deneyindeki kuantum mekaniğinin tahminlerinin gizli değişken teorileriyle (yerel gizli değişken kuramlarının) önemli ölçüde farklı olduğunu gösterdi. Kabaca söylemek gerekirse, kuantum mekaniğinin diğer eksenlerde yapılan ölçüm sonuçlarının istatiksel bağıntısı, gizli değişken teorilerindekinden daha güçlüdür. Bu farklılıklar, eşitsizlik ilişkilerini kullanan "Bell eşitsizlikleri" olarak bilinen deneysel saptanabilen prensiplerdir. Eberhard tarafından daha sonraki çalışmalarda Bell'in eşitsizliklerine öncülük eden gizli değişken kuramlarının yerelliği ve karşı-olgusal kesinlik özelliği gösterilmiştir. Bu ilkelerin geçerli olduğu herhangi bir teori eşitsizlikleri üretir. Arthur Fine sonradan eşitsizlikleri tatmin eden herhangi bir teorinin, yerel gizli değişken teorisi ile modellenebilir olduğunu göstermiştir.

Bell'in kağıt yayınlanmasından sonra, Bell eşitsizliklerini test etmek için çeşitli deneyler icat edildi. Bunlar genellikle foton kutuplaşması ölçümlerine dayanıyordu. Bugüne kadar yapılan tüm deneylerin standart kuantum mekaniği teorisinin öngörüleri doğrultusunda olduğu bulunmuştur.

Ancak Bell'in teoremi tüm olası felsefi olarak realist olan teoriler için geçerli değildir. Kuantum mekaniğinin felsefi gerçekçiliğin tüm kavramları ile tutarsız olması yaygın bir yanılgıdır. Kuantum mekaniğinin realistik yorumlaması mümkündür, fakat yukarda tartışıldığı gibi, bu tip yorumlamalar yerelliği ya da karşı-olgusal kesinliği reddeder. Ana fizik, karşı-olgusal kesinliği reddeden gerçekçilik kavramını korumak için uğraş verirken, yerelliği tutmayı da tercih eder. Böyle genel realist yorumların örnekleri, tutarlı geçmişlerini yorumlanması ve ilk kez 1986 yılında John G. Cramer tarafından önerilen işlem yorumudur. Fine'ın çalışmaları gösterdi ki, yerelliği alarak, iki istatistiksel değişken olan karşı-olgusal kesinlikler tutarsız bir şekilde ilişkilidir ve bu tür senaryolar olmasına rağmen, daha gizemli senaryoların verilmesi ile tutarsızlık karşı-olgusal kesinlik 'sezgilerde' görünebilir.

Yerelliğin ihlalin, özel görelilik ile bağdaştırmak zordur, ve nedensellik ilkesi ile uyumsuz olduğu düşünülmektedir. Ancak, Schrödinger denkleminin şartlarını biri olarak tanımlanan 'kuantum potansiyeli' şeklinde bir varsayımı yerel olmayan mekanizması tanıtılırken, kuantum mekaniğinin Bohm yorumlanması, karşı-olgusal kesinlikçe tutarlıdır. Bazı bu alanda çalışanlar gerçek deneylerde kaçamakları sömüren gizli değişken teorisini bağıntısal olarak yazmayı denemiştir.

Ayrıca, yerel gizli değişkenleri olmayan bireysel EPR benzeri deneylerin açıklaması da vardır. Örnekler David Bohm ve Lucien Hardy tarafından önerilebilir.

Einstein'ın saf cebirsel teoriye inancı

Kuantum mekaniğinin Bohm yorumlanmasına göre, evrenin durumunun, kuantum dalga işlevleri çökmeden zaman içinde sorunsuzca geliştiği varsayılmaktadır. Kopenhag yorumlanması için oluşan sorunlardan biri dalga işlevinin çöküşünün tanımlanmasıdır. Einstein kuantum mekaniğinin fiziksel olarak eksik ve mantıksal olarak yetersiz olduğunu ileri sürmüştür. "Göreliliğin Anlamı"nda Einstein, “Birisi neden gerçekliği sürekli bir alanda açıklanamayacağına iyi bir neden versin.” demiştir. Kuantum olaylarına bakıldığında, sonlu bir enerjinin sonlu bir sistemi tamamen kuantum numaraları denilen sonlu bir dizi rakamla tarif edilebilir. Bu, bir süreklilik teorisi için uygun olarak görülmemektedir ve gerçekliğin temsili için bir cebirsel teori bulma girişimine neden olmaktadır. Ama hiç kimse bu tip bir teori için bir temel bulamamıştır."Eğer zaman, mekan ve enerji Planck ölçeğinde alt tabakadan türetilmiş ikincil özellikleri ise (Bell'in teoremi hala geçerli olsa da), Einstein'ın varsayımsal cebirsel sistemi EPR paradoksunu çözmek için yeterli olabilir. Fredkin'in Sonlu Doğa Hipotezi'nde Edward Fredkin, Einstein'ın varsayımsal cebirsel sistemi için bir bilgi temeli önerdi. Eğer fiziksel gerçeklik tamamen sonlu ise, Kopenhag yorumu Planck ölçeğinde, bir bilgi işlem sistemine bir yaklaşım olabilir.

"Kabul edilebilir teoriler" ve deneyler

Durumun bugünkü görüşüne göre, kuantum mekaniği kesin bir dille kabul edilebilir herhangi bir fiziksel teorinin "yerel gerçekçiliği" yerine getirmesi gerektiğini savunan Einstein'ın yerel felsefi önermesiyle çelişmektedir.

1935 yılında yazılan EPR kağıdında, yazarlar kuantum mekaniğinin kendi varsayımları ile tutarsız olduğunu fark etmişlerdir, ama yine de Einstein kuantum mekaniğinin sadece gizli değişkenleriyle başka bir değişiklik olmadan, kabul edilebilir bir teori elde etmeyi amaçlamıştır. 1955 yılında, hayatının sonuna kadar olan yirmi yılda bu fikirleri izlemiştir.

Aksine, 1964 yılında yayınladığı kağıtta John Bell, kuantum mekaniğinin ve Einstein'ın tercih ettiği belirli bağıntılarda ³⁄₂lik katsayıya sahip gizli değişken teorisinin değişik deney sonuçlarına önderlik edebileceğini göstermiştir.

Alain Aspect'in ve diğerlerinin yaptığı birçok Bell test deneyi bulunmaktadır. Bunlar kuantum mekaniğinin tahminlerinden ziyade, Einstein tarafından desteklenen gizli değişken kuramları sınıfını desteklemektedirler.

Kuantum mekaniği için olan imalar

Çoğu fizikçi günümüzde kuantum mekaniğinin doğru olduğuna ve EPR paradoksunun klasik sezgilerin fiziksel gerçekliğe karşılık gelmemesinden dolayı sadece bir "paradoks" olduğuna inanmaktadır. EPR'nin yerellik konusunu nasıl yorumlandığı kuantum mekaniğinin kullanımlarının yorumlarına bağlıdır. Kopenhag yorumuna göre, genellikle ani dalga fonksiyonu çöküşünün meydana geldiği anlaşılmaktadır. Ancak, Kopenhag görüşünde, nedensel anlık bir etkisi olmadığı ileri sürülmüştür: Bu alternatif görüşte, ölçümler sistemin kendisini değil, fiziksel sistemdeki nicelikleri tanımlamamızı etkiler. Birçok dünyanın yorumlanmasında, bu tür ölçümlerde işlemlerin etkileri sadece ölçülen parçacığın durumunu etkilediğinden, yerellik kesinlikle korunmaktadır. Ancak, ölçüm sonuçları eşsiz değildir, her türlü sonuç elde edilebilir.

EPR paradoksu, ölçüm sürecinin temelde klasik olmayan özelliklerini açarak kuantum mekaniğine olan anlayışımızı derinleştirdi. EPR kağıdının yayınlanmasından önce, bir ölçüm genellikle ölçülen sistemin üzerine doğrudan çarptırılan fiziksel bir rahatsızlık olarak düşünülmüştür. Bir elektronun konumunu ölçerken üzerinde bir ışığın yansıdığının hayal edilmesi ve elektronu rahatsız edip ve pozisyonuna bağlı olarak kuantum mekaniksel belirsizlikleri bulmak buna örneklerdir. Kuantum mekaniğinde hala popüler olan bu tip açıklamalar, ölçümün parçacığı direkt olarak rahatsız etmeden yapılması gerektiğini gösteren EPR paradoksu tarafından çürütülmüştür. Aslında, Yagil Aharonov ve ortakları Weak ölçümleri olarak adlandırılan bir teori geliştirdiler.

Kuantum dolanmasına dayanan teknolojiler günümüzde gelişmektedirler. Kuantum şifrelemesinde, dolaşık parçacıklar iz bırakmadan ve dinlenilmeden sinyallerin iletilmesinde kullanılmaktadır. Kuantum hesaplamasında, dolaşık kuantum durumu, klasik bilgisayarlardan daha hızlı işlem yapabilen paralel hesaplamaların yapılmasında kullanılır.

Matematiksel denklemlendirim

Yukarıdaki tartışma, fırılın kuantum mekaniksel denklemlendiriminin matematiksel yazılımı olarak ifade edilebilir. Bir elektron için spin serbestlik derecesi her kuantum durumu uzayda bir vektöre denk gelen iki boyutlu karmaşık uzay vektörü olan V ile ilişkilidir. x, y, ve z yönünde fırıla karşılık gelen işlemciler, sırasıyla S_x, S_y, ve S_z şeklinde gösterilen, Pauli matrisleri kullanılarak yazılabilir.

${\displaystyle S_{x}={\frac {\hbar }{2}}{\begin{bmatrix}0&1\\1&0\end{bmatrix}},\quad S_{y}={\frac {\hbar }{2}}{\begin{bmatrix}0&-i\\i&0\end{bmatrix}},\quad S_{z}={\frac {\hbar }{2}}{\begin{bmatrix}1&0\\0&-1\end{bmatrix}}}$

Bu denklemde ${\displaystyle \hbar }$, indirgenmiş Planck sabitidir (ya da 2π'ye bölünmüş Planck sabiti.)

S_z 'nin özdurumu şu şekilde gösterilebilir;

${\displaystyle \left|+z\right\rangle \leftrightarrow {\begin{bmatrix}1\\0\end{bmatrix}},\quad \left|-z\right\rangle \leftrightarrow {\begin{bmatrix}0\\1\end{bmatrix}}}$

ve S_x 'ninki;

${\displaystyle \left|+x\right\rangle \leftrightarrow {\frac {1}{\sqrt {2}}}{\begin{bmatrix}1\\1\end{bmatrix}},\quad \left|-x\right\rangle \leftrightarrow {\frac {1}{\sqrt {2}}}{\begin{bmatrix}1\\-1\end{bmatrix}}}$

Elektron-pozitron çiftinin uzay vektörü ${\displaystyle V\otimes V}$'dür(elektronun ve pozitronun uzay vektörünün tansör çarpımı). Fırıl tekil durumu;

${\displaystyle \left|\psi \right\rangle ={\frac {1}{\sqrt {2}}}{\bigg (}\left|+z\right\rangle \otimes \left|-z\right\rangle -\left|-z\right\rangle \otimes \left|+z\right\rangle {\bigg )}}$

bu denklemde sağ taraftaki iki terim daha önceden durum 1 ve durum 2 olarak tanımladığımız niceliklerdir.

Yukardaki denklemden fırıl tekilinin ayrıca şu şekilde yazılabileceğini görebiliriz;

${\displaystyle \left|\psi \right\rangle =-{\frac {1}{\sqrt {2}}}{\bigg (}\left|+x\right\rangle \otimes \left|-x\right\rangle -\left|-x\right\rangle \otimes \left|+x\right\rangle {\bigg )}}$

yine sağ taraftaki terimler durum 1a ve durum 2a olarak tanımladığımız niceliklerdir.

Bunun nasıl yerel gerçekliği ihlal ettiğini anlamak için, Alice'in S_z veya S_x ölçümünden sonra, Bob'un S_z veya S_x değerinin tek olarak tanımlanmasıdır ve bu "fiziksel gerçekliğin elementi"ne denk gelir. Bu, kuantum mekaniğindeki ölçümlerin prensibiyle alakalıdır. S_z değeri ölçüldüğünde, sistem durumu olan ψ S_z'in özvektöründe çöker. Eğer ölçümlerin sonucu +z ise, ölçümden hemen sonra sistem durumu ψ'ın dikey çıkıntısına maruz kalır ve şu formu alır;

${\displaystyle \left|+z\right\rangle \otimes \left|\phi \right\rangle \quad \phi \in V}$

Fırıl tekili için yeni durum;

${\displaystyle \left|+z\right\rangle \otimes \left|-z\right\rangle }$

Aynı şekilde, eğer Alice'in ölçüm sonucu −z çıkarsa, sistem dikey çıkıntıya maruz kalır;

${\displaystyle \left|-z\right\rangle \otimes \left|\phi \right\rangle \quad \phi \in V}$

bu, yeni durumun aşağıdaki gibi olduğunu gösterir;

${\displaystyle \left|-z\right\rangle \otimes \left|+z\right\rangle }$

Bu, S_z için yapılan ölçümde Bob'un pozitronunun tanımlandığına ve ilk durumda −z veya ikinci durumda +z olduğu anlamına gelir.

S_x ve S_z, kuantum mekaniğinde kesin sonuçlara sahip olamaz. Aralarından biri işlemcilerin değişmemesi unsurunu kullanabilir;

${\displaystyle \left[S_{x},S_{z}\right]=-i\hbar S_{y}\neq 0}$

Heisenberg belirsizlik ilkesi ile birlikte;

${\displaystyle \left\langle {\Delta S_{x}}^{2}\right\rangle \left\langle {\Delta S_{z}}^{2}\right\rangle \geq {\frac {1}{4}}\left|\left\langle \left[S_{x},S_{z}\right]\right\rangle \right|^{2}}$

Kaynakça

"EPR Paradox". 6 Kasım 2015 tarihinde kaynağından arşivlendi. http://web.archive.org/web/20151106192508/https://en.wikipedia.org/wiki/EPR_paradox.