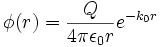Elektrik alan perdelemesi
Perdeleme, hareketli yük taşıyıcılarının varlığından ortaya çıkan elektrik alanının sönümünü ifade eder. Metaller ve yarıiletkenlerdeki iletim elektronları ve iyonize olmuş gazlar(klasik plazma) gibi yük taşıyıcı akışkanlarda gözlemlenir. Elektriksel olarak yüklenmiş parçacıklardan oluşan bir akışkanda, her çift parçacık Coulomb kuvveti ile etkileşir,
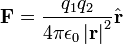 .
.
Bu etkileşim akışkanın teorik davranışını karmaşık hale getirir. Mesela, temel seviye enerji yoğunluğunun salt kuantum mekaniksel hesabı sebepsiz olarak sonsuza gider. Buradaki zorluk; Coulomb etkisi 1/r² ile azalmakla beraber, her r mesafesindeki parçacıkların ortalama sayısının r² ile orantılı olmasıdır(akışkanın izotropik olduğu varsayılmaktadır). Sonuç olarak, bir noktadaki yük dalgalanması uzak mesafelerde ihmal edilebilir değildir.
Gerçekte, uzun menzilli etkiler elektrik alanlara duyarlı akışkan parçacıklarının akımı ile söner. Bu akım parçacıklar arası etkin etkileşimi kısa menzilli "perdelenmiş" Coulomb etkileşimine indirger.
Elektronlardan oluşan bir akışkanı ele alalım. Her elektron diğer elektronları itecek bir elektrik alana sahiptir. Sonuçta, elektronun çevresi normal durumdan daha düşük elektron yoğunluğuna sahip olacaktır. Bu bölge pozitif yüklenmis "perdeli boşluk" olarak algılanabilir. Uzak mesafelerden bakıldığında bu perdeli boşluk, elektronlar tarafından üretilen elektrik alanı ortadan kaldıran bir positif yükünki ile eşdeğer etkiye sahiptir. Boşluk bölgesi içinde elektronun ürettiği alan sadece kısa mesafelerde tespit edilebilecektir.
Electrostatik perdeleme
Perdeleme olgusuna ilk teorik bakış, Debye ve Hückel (1923) tarafından, akışkan içine gömülü durağan noktasal bir yükle başlar. Bu olguya electrostatik perdeleme adı verilir.
Arka zemini ağır ve pozitif yüklü iyonlardan oluşan, içi elektron dolu bir akışkan hayal edelim. Basitçe, hareketini ve mesafeye bağlı dağılımını ihmal ettiğimiz iyonların arka zeminde düzenli bir yük dağılımına sahip olduklarını varsayalım. Bu varsayım, elektronlar iyonlara nazaran daha hafif, daha hareketli oldukları için geçerlidir. Bu varsayıma göre elektronlar arası mesafe iyonlar arası mesafeden dahabüyüktür. Yoğun madde fiziğinde, anlattığımız bu modele jel modeli denilmektedir.
ρ (elektronların) parçacık yoğunluğu, φ electrik potansiyelidir. İlk etapta, elektronlar uzayda eşit olarak dağıldığı için her noktada net yük sıfırdır. Böylece φ başlangıçta sabittir.
Sistemin merkezine hareketsiz duran nokta Q yükü yerleştirirsek, buna bağlı yük yoğunluğu Qδ(r) olur. δ(r) Dirac delta fonksiyonudur. Sistem denge durumuna döndüğünde elektron yoğunluğu ve elektrik potansiyelindeki değişiklikler sırasıyla Δρ(r) ve Δφ(r) olur. Elektron yoğunluğu ve elektrik potansiyeli Maxwell eşitliklerinin ilki ile ilişkilendirilir,
![- \nabla^2 [\Delta\phi(r)] = \frac{1}{\epsilon_0} [Q\delta(r) - e\Delta\rho(r)]](../I/m/4389b86dc8b5261ccd4a9b2de1fbccbb.png) .
.
Teoriyi geliştirmek içn, Δρ ve Δφ ile ilgili ikinci bağımsız bir denkleme ihtiyaç vardır. İki parametrenin orantılı olduğu iki olası yaklaşım: Debye-Hückel yaklaşımı(yüksek sıcaklıklar için) ve Fermi-Thomas yaklaşımıdır (düşük sıcaklıklar için).
Debye-Hückel yaklaşımı
Debye-Hückel yaklaşımında, sistemi termodinamik dengede; akışkan parçacıklarının Maxwell-Boltzmann staistatistiğini sağlayacak bir T sıcaklığında tutatrız. Uzayın her bir noktasında j enerjili elektronların yoğunluğunun ifadesi
burada kB Boltzmann sabitini ifade eder. φ yi rahatsız edersek ve exponensiyel ifadeyi birinci dereceden açarsak, elde edeceğimiz ifade
olur ki, bu eşitlikte
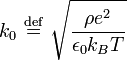 .
.
Denklemde yer alan uzunluk λD ≡ 1/k0 Debye uzunluğu olarak adlandırılır. Debye uzunluğu klasik plazmada temel uzunluk ölçüsüdür.
Fermi-Thomas yaklaşımı
Fermi-Thomas yaklaşımında, sistem sabit bir kimyasal potansiyel ve düşük bir sıcaklıkta bırakılır (bahsedilen koşul gerçek bir deneyde, taban durumu elektrik ile sabit potansiyel farkına sahip bir elektrik kontağındaki akışkanın korunmasına karşılık gelir). Kimyasal potansiyel μ tanım olarak akışkana eklenen ilave bir elektronun enerjisini ifade eder. Bu enerji, kinetik enerji T ve potansiyel enerji -eφ olarak iki parçadan oluşabilir. Kimyasal potansiyel sabit tutulduğunda,
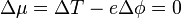 .
.
Eğer sıcaklık yeterince düşükse, elektronların davranışı kuantum mekaniksel bir model olan ""serbest elektron gazı""na yaklaşır. Böylece serbest elektron gazında yer alan ilave bir elektronun kinetik enerjisini ifade eden T Fermi enerjisi EF olur. Fermi enerjisinin elektron yoğunluğu ile ilişkisi (spin dejeneresini de içerir)
Birinci dereceden pertürbasyonda bulacağımız ifade
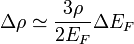 .
.
Bunu bir önceki eşitlikte yerine koyarsak Δμ için elde edeceğimiz denklem
burada
bu eşitlik Fermi-Thomas perdeleme dalga vektörü olarak adlandırılır.
Eetkileşimsiz elektron modeli olan serbest elektron gazı için önceden türetilmiş denklemler eled edildi. Hâlbuki üzerinde çalışılan akışkan, Coulomb etkileşimini içermektedir. Yani Fermi-Thomas yaklaşımı, elektron yoğunluğunun çok yüksek olduğu ve böylece parçacık etkileşimlerinin nispeten zayıf olduğu durumlarda geçerlidir.
Perdelenmiş Coulomb etkileşimleri
Debye-Hückel ya da Fermi-Thomas yaklaşımları ile elde edilen sonuçlar birinci Maxwell eşitliği içine yerleştirilebilir. Sonuç
bu denklem perdelenmiş Poisson denklemi olarak bilinir. Dnklemin çözümü
bu ifade perdelenmiş Coulomb potansiyeli olarak adlandırılır. Bu, eksponensiyel sönüm terimi ile çarpılmış bir Coulomb potansiyelidir. Sönüm faktörü k0 ile ifade edilir ve Debye ya da Fermi-Thomas dalga vektörü olarak adlandırılır. Bahsedilen potansiyelin şekli Yukawa potansiyeline benzemektedir. Bu perdeleme, dielectrik fonksiyonunu 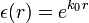 verir.
verir.
Kuantum-mekaniksel perdeleme
Gerçek metallerde, elektriksel perdelemenin fiziksel tanımı Fermi-Thomas teorisindekinden daha karmaşıktır. Bu karmaşıklık, Fermi-Thomas teorisinde hareketli yüklerin (elektronlar) herhangi bir dalga vektörü değerinde tepki verdiğini farzetmemizden kaynaklanır. Aslında, Fermi yüzeyi içinde ya da üzerinde yer alan bir elektronun Fermi dalga vektöründen daha kısa dalga vektörlerinde tepki vermesi beklenemez. Bu Gibbs fenomeni ile ilgilidir. Bu fenomene göre, uzayda hızlı değişimler sergileyen fonksiyonların fourier serileri, seride yer alan birçok terimi gözönüne almadan yapılan hesaplarda iyi bir yaklaşım sayılamaz. Fizikte bunlara Friedel salınımları denir ve yüzey ile yığın perdelemesinde kullanılır. Her durumda, net elektrik alan uzayda eksponansiyel bir düşüş göstermez.
![\rho_j (r) = \rho_j^{(0)}(r) \; \exp\!\left[\frac{e\phi(r)}{k_B T}\right]](../I/m/0d06568f176a7a18ead27d4c50cd2cca.png)
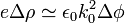
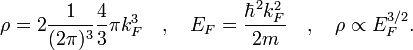
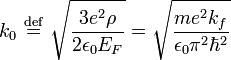
![\left[ \nabla^2 - k_0^2 \right] \phi(r) = - \frac{Q}{\epsilon_0} \delta(r)](../I/m/b380fc87e7dd6cf69f216b8a011acc8c.png)