Elektron dizilimi

Elektronların atomik ve moleküler orbitalleri

Lityum atomunun Bohr diyagramı

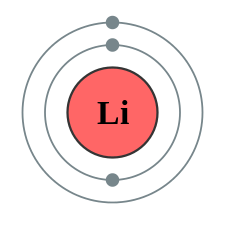
Elektron dizilimi, atom fiziği ve kuantum kimyasında, bir atom ya da molekülün (ya da diğer fiziksel yapıların) elektronlarının atomik ya da moleküler orbitallerdeki dağılımıdır. Örneğin Neon atomunun elektron dizilimi  1s² 2s² 2p⁶ olarak gösterilir.

Elektron diziliminde elektronlar her biri bağımsız bir şekilde yörüngelerde hareket eden atom altı parçacıklar olarak tanımlanmışlardır. Matematiksel olarak bu dizilim Slater determinantı ya da durum fonksiyon dizilimi olarak belirtilir

Kuantum mekaniğinin kurallarına göre tek elektronlu sistemlerde enerji bu elektronun konumuyla ilişkilidir. Belirli koşullar altında, elektronlar bir konumdan başka bir konuma hareket edebilir. Bu hareket foton formunda olan kuantumlanmış enerjinin ışıma ya da soğurma yapmasıyla gerçekleşebilir.

Periyodik tablodaki elementlerin yapısını anlama süreci içerisinde, birbirinden farklı olan bu atomların elektron dizilimlerine dair bilgiler oldukça yararlıdır. Bu fikir ayrıca atomları bir arada tutan kimyasal bağları tasvir etmeye olanak sağlar. Yine bu fikir, lazerlerin ve yarı iletkenlerin kendine has özelliklerinin açıklanmasına imkan sunar.

Kabuklar ve Alt Kabuklar

s (l=0)	p (L=1)
m=0	m=0	1 m=±
s	pz	px	py
1 n=
2 n=

Elektron dizilimi ilk olarak Bohr atom modeline göre tasarlanmıştır. Elektronun kuantum mekaniksel gerçekliğini anlamadaki ilerlemelere rağmen, Bohr atom modelinin elektron kabuğu ve alt kabuklara dair belirttiği ifadeler hala geçerlidir. 

Bir elektron kabuğu aynı baş kuantum sayısını (n) paylaşan kuantum durum dizisidir. Baş kuantum sayısı n ile gösterilir ve n burada orbital olarak ifade edilen harften önceki sayı olarak belirtilir. Elektron kabuğu elektronların dolanabildiği bir alandır. Bir atomun n’inci elektron kabuğu  2n² kadar elektron yerleştirebilir. Örneğin ilk kabuğa 2 elektron, ikinci kabuğa 8 elektron ve üçüncü kabuğa 18 elektron yerleştirebilir. İzin verilen durum elektron spininden dolayı ikiye katlanmaktadır. Her bir atom orbitalinin spinleri zıt olmak üzere iki elektronun aynı kuantum sayılarına sahip olduğu görülmektedir, bunlardan biri +1/2 spinine sahipken (genellikle yukarıya doğru bir ok şeklinde gösterilir) diğeri -1/2 spinine sahiptir.( -1/2 spini de aşağı doğru ok şeklinde gösterilir.)

Bir alt kabuk, kendisini kapsayan kabuk içerisinde, açısal momentum kuantum sayısı ile ifade edilen bir konum dizisidir. ℓ =  0, 1, 2, 3 değerleri sırasıyla s,p,d,f orbitalleri olarak gösterilir. Bir alt kabukta konumlandırılacak maksimum elektron sayısı 2(2ℓ + 1) formülü ile bulunabilir. Bu formül, s alt kabuğunda maksimum 2 elektron olabileceğini, p alt kabuğunda maksimum 6 elektron, d alt kabuğunda maksimum 10 elektron, f alt kabuğunda da maksimum 14 elektron bulunabileceğini göstermektedir.

Bir kabuk veya alt kabukta ne kadar elektronun bulunabileceği kuantum mekaniği denklemlerinden çıkarılmaktadır. Özellikle Pauli dışlama ilkesinden dolayı, aynı atom içerisinde bütün kuantum sayıları aynı olan iki elektronun mümkün olamayacağı ifade edilmiştir. 

Gösterim

Fizikçiler ve kimyacılar atom ve moleküllerin elektron dizilimlerini göstermek için standart gösterim tipini kullanırlar. Atomlar için bu gösterim, atom orbitalleri dizisi ile (örneğin Fosfor elementi için 1s, 2s, 2p, 3s, 3p) her bir orbitale ait elektron sayısı ile ifade edilir. Elektron sayısı orbitalin üst indisine yazılır. Örneğin hidrojen atomunun birinci kabuğundaki s orbitalinde yalnızca 1 elektron vardır, dolayısıyla hidrojen atomunun elektron dizilimi 1s1 gösterimi ile ifade edilir. Lityum atomunun 1s alt kabuğunda 2 elektron vardır, daha üst enerji seviyesi olan 2s alt kabuğunda ise 1 elektron vardır, böylelikle Lityum atomunun elektron dizilimi 1s² 2s¹ gösterimi (okunuşu ise “bir-s-iki, iki-s-bir ) ile ifade edilir.. Atom numarası 15 olan Fosfor elementinin elektron dizilimi ise şöyledir: 1s² 2s² 2p⁶ 3s² 3p³.

Çok fazla elektrona sahip olan atomlar için bu gösterim şekli çok uzun olabilir bundan dolayı kısaltılmış gösterimler kullanılır. Çünkü daha önce ifade edilmiş bütün alt kabuklar (son alt kabuklardan bazıları için söyleyebiliriz bunu ) asal gazlardan herhangi birinin elektron dizilimiyle aynıdır. Örneğin Fosfor elementi Neon elementinden ( Neon’un elektron dizilimi 1s² 2s² 2p⁶ şeklindedir) sadece üçüncü kabuğu olması bakımından farklılık taşır. Böylelikle, Neon elementinin elektron dizilimi çekip alınır ve Fosfor elementinin elektron dizilimi şöyle yazılır:  [Ne] 3s² 3p³. Bu düzenleme, elementlerin kimyasını en dış kabuktaki elektronlar belirlediği için oldukça yararlıdır.

Verilmiş bir dizilim için, orbitalleri yazma sırası sabit değildir yalnızca dolu orbitaller fiziksel öneme sahiptir. Örneğin temel haldeki Titanyum elementinin elektron dizilimi  [Ar] 4s² 3d² ya da [Ar] 3d² 4s² şeklinde yazılabilir. İlk gösterim şekli nötr atomların dizilimine uygun olan Madelung ilkesine dayandırılarak yazılmıştır. 4s orbitali Ar, K, Ca, Sc, Ti elementlerinde 3d orbitalinden önce doldurulur. İkinci gösterim şeklinde, atomlar pozitif iyon haline gelebilmek için elektronları orbital enerjisinin tersiyle orantılı bir sıra içinde uzaklaştırırlar. Ti⁴⁺, Tı⁺³, Ti⁺², Ti⁺,Ti serisinde, 3d orbitali 4s orbitalinden önce doldurulur.

Tek elektrona sahip orbitallerde üst indis olan 1’i yazmak zorunlu değildir. Orbitalleri tanımlayan s,p,d,f harflerini italik ya da eğik olarak yazmak oldukça yaygındır. Uluslararası Temel ve Uygulamalı Kimya Birliğinin orbital harflerinin normal yazı tipiyle yazılmasına dair önerilerine rağmen bu harflerin italik ya da eğik olarak yazılması yaygındır. Bu harflerin kökeni tayf çizgilerini kategorileştirme sisteminden gelmektedir. “sharp” ,” principal” “diffuse” ve “fundamental”. Bu sistem ince yapı gözlemlerine dayanmaktadır. Bunların güncel kullanımı açısal momentum kuantum sayısı olan l nin değerleri 0, 1, 2 ya da 3’ü belirtir. “f” harfinden sonra ise bu dizi alfabetik olarak “g”, “h” “i” … (l = 4, 5, 6) olarak devam eder. Nadiren ihtiyaç duyulsa da “i” harfinden sonra j’ye geçilir. 

Moleküllerin elektron dizilimi de buna benzer bir yolla yazılır. Aradaki fark, atomik orbital yerine moleküler orbital kullanılmasıdır (alt kısımda görebilirsiniz).

Enerji – Temel Hâl ve Uyarılmış Hâl

Elektronun enerjisi onun orbitaliyle ilgilidir. Elektron-elektron etkileşimi ihmal edilirse, bir dizilimin yaklaşık enerjisi her bir elektronun enerjilerinin toplamı alınarak belirlenebilir. En düşük elektronik enerji dizilimi temel hâl olarak adlandırılır. Diğer dizilimler ise uyarılmış hâli belirtir. 

Örnek verilecek olursa, Sodyum atomunun temel hâldeki elektron dizilimi Aubau kuralı (alt kısımda görebilirsiniz) dikkate alınacak olursa 1s² 2s² 2p⁶ 3s şeklindedir. İlk uyarılmış hâl, 3s orbitalindeki elektronu 3p orbitaline göndererek yapılır. Böylelikle 1s² 2s² 2p⁶ elektron dizilimi elde edilmiş olur. Atomların sahip oldukları elektron dizilimleri soğurma ve ışıma enerjisi ile değişebilir. Örneğin, Sodyum buharı lambasında, Sodyum atomları elektriksel boşalma vasıtasıyla 3p orbital seviyesine uyarılmışlardır. Daha sonra dalga boyu 589 nanometre olan sarı bir ışık yayarak temel hâline geri dönerler.

Değerlik elektronları uyarmak için (sodyum atomundaki 3s orbitali gibi ) genellikle görülebilen ışınların ya da mor ötesi ışınların enerjisi gereklidir. Çekirdek elektronlarının da uyarılabilmesi mümkündür fakat bunun için x-ray fotonları gibi yüksek enerjiler gereklidir. 2p orbitalindeki elektronu 3s orbital seviyesine uyararak  1s² 2s² 2p⁵ 3s² elektron dizilimi böylelikle gerçekleşebilir.

Bu yazının geri kalanı yalnızca temel hâl ile ilgili olacaktır ve bu temel hâl sıklıkla atom ya da molekülün elektron dizilimi olarak tanımlanacaktır. 

Tarihi

Elementlerin özelliklerinde periyotluğun atomun elektronik yapısıyla açıklanabileceği fikri ilk olarak Niels Bohr (1923) tarafından önerilmiştir. Onun önerileri Bohr Atom Modeline dayandırılmıştır. Bohr atom modelinde elektron kabukları çekirdekten sabit bir uzaklıktaki yörüngeler olarak tanımlanmıştır. Bohr Atom Modelinin elektron dizilim gösterimi günümüz kimyasına oldukça yabancıdır. Örneğin Sülfür atomunun elektron dizilimi  1s² 2s² 2p⁶ 3s² 3p⁴ (2.8.6) olarak değil; 2.4.4.6 olarak gösterilir

İlerleyen yıllarda Edmund Clifton Stoner, Arnold Sommerfeld’in elektron kabuğuna dair üçüncü kuantum sayısı tanımlamasını birleştirdi ve Sülfür elementinin kabuk yapısının 2.8.6 olduğunu doğru bir şekilde tahmin etti. Ama Bohr’un atom modeli de Stoner’ın atom modeli de bir manyetik alandaki atomik spektrum değişimleri tanımlayamamıştır.

Bohr bu eksikliğin gayet farkındaydı (diğer bilim adamları da) ve arkadaşı Wolfgang Pauili’ye kuantum teorisinin (bu sistem bugün “eski kuantum teorisi” olarak bilinir ) ihmal edilmemesi için yardım istedi. Pauli, Zeeman etkisinin yalnızca atomun en dış elektronlardan kaynaklanabileceğini farketti ve Stoner’in kabuk yapısına dair teorisini yeniden değerlendirdi. Bu yeni değerlendirmede dördüncü kuantum sayısı ve Pauli dışlama ilkesi eklenerek alt kabukların doğru yapısı belirlendi (1925) :

Baş kuantum sayısı (n) ve diğer üç kuantum numarası (k [l], j [ml] ve m [ms]) aynı olan iki elektronun varlığı mümkün değildir.

 

1926 yılında yayımlanan Schrödinger denklemi, hidrojen atomunun anlaşılır hale gelmesinin sonucu olarak dört kuantum numarasından üçünü verdi. Bu sonuç günümüzde kullanılan kimya kitaplarında da belirtildiği gibi atomik orbitalin nasıl olduğuna dair bilgiler sağladı. Atom spektrumu incelemeleri, atomların elektron diziliminin deneysel olarak belirlenmesini sağladı. Ayrıca atomun orbitallerinin elektronlarla nasıl dolduğuna dair deneysel bir kural ( Madelung kuralı olarak bilinir (1936) ) verdi. 

Atomlar: Aufbau İlkesi ve Madelung Kuralı

Aufbau (Almanca inşaa etmek anlamında) ilkesi, Bohr’un elektron dizilimine dair orijinal fikrinin bir parçasıdır. Şöyle açıklanabilir :

En fazla iki elektron bir orbitale yerleştirilebilir. Elektronlar düşük enerjili orbitallerden yüksek enerjili orbitallere sırayla yerleştirilir. 

Atom orbitallerinin elektronlar tarafından doldurulma sırası 1s'den 7p'ye uzanan ok ile takip edilir.

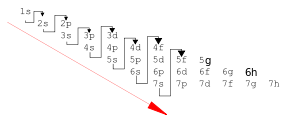
Bu ilke ilk 18 elementi gayet iyi açıklayabilmektedir. (atomların uyarılmamış halleri için) Fakat bu 18 elementten sonra ilerlenilen her adımda elementleri açıklayabilme yetisi giderek azalmaktadır. Aufbau ilkesinin modern formu Madelung kuralı tarafından belirlenen orbital enerjisi sıralamasını tanımlayabilmektedir. Bu kural ilk olarak 1929 yılında Charles Janet tarafından dile getirildi. 1936 yılında ise Erwin Madelung yeniden keşfetti. Daha sonra V.M Klechkowski tarafından teorik bir temele dayandırıldı. 

1. Orbitaller artan n+l değeri sırasına göre doldurulurlar
2.  n+l değerinin aynı olması durumunda orbitaller artan n değerine göre sırayla doldurulur

Aşağıdaki dizilim orbitallerin doldurulma sırasını göstermektedir:

1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, 7p, (8s, 5g, 6f, 7d, 8p ve 9s)

Listede parantez içerisinde ifade edilmiş orbitaller ağır atomların (Ununoktiyum Z = 118) temel hallerinde bulunamazlar.

Aufbau kuralı, değiştirilmiş haliyle atom çekirdeğindeki proton ve nötronlara uygulanabilir, çekirdek fiziği ve kimyasının kabuk modeli için.

Periyodik tablo

Elektron dizilim tablosu

Periyodik tablonun şekli atomların elektron dizilimiyle son derece ilişkilidir. Örneğin, 2. grup elementlerinin hepsi [E] ns² elektron dizilimine sahiptir. (E burada bir asal gazın elektron dizilimidir) Ayrıca bunlar aynı grupta oldukları için kimyasal özellikleri bakımından önemli ölçüde birbirine benzemektedirler. Daha genel olarak, periyodik tablodaki blok kavramının nedeni s,p,d,f alt kabuklarını doldurmak için gerekli elektron sayısıdır. ( 2,6,10,14…)

En dış elektron kabuğuna genellikle “değerlik kabuğu” denilmektedir. Bu kabuk atomun kimyasal özelliğini belirlemektedir. Hatırlanmalı ki daha önceden, kimyasal özelliklerdeki benzerlikler elektron dizilimi düşüncesinden daha önemliydi.   

Aufbau ilkesinin eksiklikleri

Aufbau ilkesi, orbital enerjilerinin sabit bir sırada olduğu koşulları kapsamaktadır. Herhangi bir element ve farklı iki element arasındaki durumlarda bu ilke yalnızca yaklaşık olarak doğru sonuç verebilir. Atom orbitalleri iki elektronun nasıl yerleştirileceğine dair “sabit bir enerji kutusu” gibi varsayılan bir durumdur. Ama bir atom orbitalindeki elektronun enerjisi aynı zamanda atomun (iyon ya da molekül de olabilir) sahip olduğu diğer elektronların enerjisine de bağlıdır. Birden fazla elektrona sahip sistemler için bir elektronlu sistemin analizi yanlıştır.( Hartree-Fock gibi çeşitli matematiksel yaklaşımlar olmasına rağmen çözüm tam olarak hesaplanamaz).

Aufbau ilkesi tahmine dayanmaktadır. Bir kabuk içerisinde s orbitalleri her zaman p orbitallerinden önce doldurulur. Tek bir elektrona sahip olan hidrojen atomu ve benzerlerinde, aynı kabuğun s ve p orbitalleri tamamıyla aynı enerjiye sahiptir. Dış elektromanyetik alan olmadığı zaman oldukça iyi yaklaşımlar verir. ( ama bir hidrojenin atomunun enerji seviyeleri gerçekte çekirdeğin manyetik alanı tarafından bölünür, bu durum Lamb kaymasının kuantum elektrodinamik etkisiyle açıklanabilir )

Geçiş metallerinin iyonlaşması

Aufbau ilkesinin uygulaması popüler bir paradoksa yol açar. Bu paradoks geçiş metallerinin basit kimyasıyla ilgilidir. Potasyum ve kalsiyum elementleri periyodik tabloda geçiş metallerinden önce gelir. Bu elementler sırasıyla  [Ar] 4s¹ ve [Ar] 4s² elektron dizilimlerine sahiptir. Yani 4s orbitali 3d orbitalinden önce doldurulmaktadır. Bu durum Madelung kuralıyla açıklanabilmektedir çünkü 4s orbitali n+l = 4 (n=4 l=0 ) değerine sahipken, 3d orbitali n+l=5 (n=3 l=2) değerine sahiptir. Kalsiyum elementinden sonra, geçiş metallerinin ilk serisindeki çoğu nötr atomun (Sc-Zn) 4s orbitalinde 2 elektron vardır fakat buna istisna bir durum söz konusudur. Krom ve bakır elementleri sırasıyla  [Ar] 3d⁵ 4s¹ ve [Ar] 3d¹⁰ 4s¹ elektron dizilimlerine sahiptir. Yani bir elektron yarı dolu ya da tam dolu alt kabuk olabilmesi için 4s orbitalinden 3d orbitaline geçmektedir. Bu durumda, elektronun kararlı bir dizilime sahip olabilmek için alt kabukları yarı dolu ya da tam dolu tercih ettiği görülür.

Bu geçiş metallerini iyonlaştırmak için bir elektron uzaklaştırdığımızda paradoks ortaya çıkar. İyonlaşmak için uzaklaştırılan ilk elektron 3d orbitalinden gelmez. 3d orbitali daha yüksek enerjide olduğu için böyle bir tahmin yapılabilir fakat iyonlaşmak için uzaklaştırılan ilk elektron 4s orbitalinden gelir. 4s ve 3d orbitallerindeki bu elektron değiş-tokuşu geçiş metallerinin ilk serisindeki tüm atomlar için söylenebilir. Nötr atomların (K, Ca, Sc, Ti, V, Cr… ) elektron dizilimi her zaman 1s ,2s, 2p, 3s, 3p, 4s, 3d sıralamasını takip eder. Fakat bir atomun peş peşe iyonlaşma aşamalarında (örneğin  Fe²⁺, Fe³⁺, Fe²⁺, Fe⁺, Fe) 1s, 2s, 2p, 3s, 3p, 3d, 4s … sıralaması takip edilir. 

Eğer atom orbitallerinin enerji sıralamasının sabit olduğu ve bunların çekirdek yükü tarafından ya da diğer orbitallerdeki elektronlar tarafından etkilenmediği varsayılırsa bu olay sadece paradoksal olarak değerlendirilir. Eğer böyle olsaydı, 3d orbitali 3p orbitaliyle aynı enerjide olurdu hidrojen atomunda olduğu gibi, fakat durum böyle değildir. Fe2+ iyonunun krom atomuyla aynı elektron dizilimine sahip olması için herhangi özel bir neden yoktur. Demir elementi çekirdeğinde krom atomundakinden 2 adet daha fazla proton vardır ve bu iki türün kimyası oldukça farklıdır. 

3d^x4s⁰ elektron dizilimine sahip iyonlar kompleks geçiş metallerinde görülür. Metal 0 yükseltgenme seviyesine sahip olsa bile bu olay kristal alan teorisi ile basit bir şekilde tanımlanabilir. Örneğin krom hexa karbonil, çevresi altı adet karbon monoksit ligand ile çevrili krom atomu olarak belirtilebilir. Merkezi krom atomunun elektron dizilimi 3d6 nın altı elektronunun ligandlar arasındaki üç düşük enerjili d orbitallerini doldurduğu şekilde tanımlanabilir. Diğer iki d orbitali ise ligandların kristal alanlarından dolayı yüksek enerjidedir. Bileşik diyamanyetiktir, yani eşlenmemiş elektronu yoktur ve bu tablo deneysel gerçeklerle tutarlıdır. Fakat daha doğru bir yaklaşıma sahip olan moleküler orbital teoriye göre altı elektron tarafından doldurulan d orbitalleri, tek bir atomun d orbitalleriyle aynı özellikte değildir.

Madelung Kuralının diğer eksiklikleri

Ağır atomlar arasında bazıları Madelung kuralına uymaz. Bundan dolayı bunlar hakkında “kararlı hale gelebilmek için yarı dolu alt kabuk” gibi basit bir açıklama yapmak çok ama çok zordur. Bu kurala uymayan çoğu istisnai durum Hartree-Fock hesaplamaları ile tahmin edilebilir. Bu metot orbital enerjisindeki diğer elektronların etkisini dikkate alan yaklaşık bir metottur. İç kabuk elektronları ışık hızına yakın hızlarda hareket ederken, özel göreliliğin atom orbitalinin enerjisindeki etkisi dikkate alınmalıdır, özellikle ağır atomlar için. Daha genel olarak bu relavistik etki, s orbitallerini diğer atom orbitallerine göre daha düşük enerjiye yöneltir. Aşağıdaki tablo elementlerin temel hal dizilimlerini orbitallerin dolumuna göre göstermektedir. Fakat bu tablo, elementlerin temel hallerini orbital enerjilerinin dizisi cinsinden göstermez. Örneğin, 4s orbitali geçiş metallerinde 3d orbitallerinden daha yüksek enerjiyi temsil eder. Ayrıca lantanitlerde 6s orbitali 4f ve 5d orbitallerinden daha yüksek enerjilidir. 

Electron shells filled in violation of Madelung's rule^[1] (red)

Period 4			Period 5			Period 6			Period 7
Element	Z	Electron Configuration	Element	Z	Electron Configuration	Element	Z	Electron Configuration	Element	Z	Electron Configuration
Lanthanum	57	[Xe] 6s^2 5d^1	Actinium	89	[Rn] 7s^2 6d^1
Cerium	58	[Xe] 6s^2 4f^1 5d^1	Thorium	90	[Rn] 7s^2 6d^2
Praseodymium	59	[Xe] 6s^2 4f^3	Protactinium	91	[Rn] 7s^2 5f^2 6d^1
Neodymium	60	[Xe] 6s^2 4f^4	Uranium	92	[Rn] 7s^2 5f^3 6d^1
Promethium	61	[Xe] 6s^2 4f^5	Neptunium	93	[Rn] 7s^2 5f^4 6d^1
Samarium	62	[Xe] 6s^2 4f^6	Plutonium	94	[Rn] 7s^2 5f^6
Europium	63	[Xe] 6s^2 4f^7	Americium	95	[Rn] 7s^2 5f^7
Gadolinium	64	[Xe] 6s^2 4f^7 5d^1	Curium	96	[Rn] 7s^2 5f^7 6d^1
Terbium	65	[Xe] 6s^2 4f^9	Berkelium	97	[Rn] 7s^2 5f^9
Scandium	21	[Ar] 4s^2 3d^1	Yttrium	39	[Kr] 5s^2 4d^1	Lutetium	71	[Xe] 6s^2 4f^14 5d^1	Lawrencium	103	[Rn] 7s^2 5f^14 7p^1
Titanium	22	[Ar] 4s^2 3d^2	Zirconium	40	[Kr] 5s^2 4d^2	Hafnium	72	[Xe] 6s^2 4f^14 5d^2	Rutherfordium	104	[Rn] 7s^2 5f^14 6d^2
Vanadium	23	[Ar] 4s^2 3d^3	Niobium	41	[Kr] 5s^1 4d^4	Tantalum	73	[Xe] 6s^2 4f^14 5d^3
Chromium	24	[Ar] 4s^1 3d^5	Molybdenum	42	[Kr] 5s^1 4d^5	Tungsten	74	[Xe] 6s^2 4f^14 5d^4
Manganese	25	[Ar] 4s^2 3d^5	Technetium	43	[Kr] 5s^2 4d^5	Rhenium	75	[Xe] 6s^2 4f^14 5d^5
Iron	26	[Ar] 4s^2 3d^6	Ruthenium	44	[Kr] 5s^1 4d^7	Osmium	76	[Xe] 6s^2 4f^14 5d^6
Cobalt	27	[Ar] 4s^2 3d^7	Rhodium	45	[Kr] 5s^1 4d^8	Iridium	77	[Xe] 6s^2 4f^14 5d^7
Nickel	28	[Ar] 4s^2 3d^8 or [Ar] 4s^1 3d^9 (disputed)[2]	Palladium	46	[Kr] 4d^10	Platinum	78	[Xe] 6s^1 4f^14 5d^9
Copper	29	[Ar] 4s^1 3d^10	Silver	47	[Kr] 5s^1 4d^10	Gold	79	[Xe] 6s^1 4f^14 5d^10
Zinc	30	[Ar] 4s^2 3d^10	Cadmium	48	[Kr] 5s^2 4d^10	Mercury	80	[Xe] 6s^2 4f^14 5d^10

Moleküllerin Elektron Dizilimi

Elektron dizilimi söz konusu molekül olduğunda daha karmaşıktır çünkü her molekül farklı orbital yapıya sahiptir. Atom orbitalindeki sınıflandırmadan farklı olarak molekül orbitalleri simetrilerine göre sınıflandırılır. Bundan dolayı dioksijen molekülünün elektron dizilimi, O₂, 1σ_g² 1σ_u² 2σ_g² 2σ_u² 3σ_g² 1π_u⁴ 1π_g²  şeklinde ya da 1σ_g² 1σ_u² 2σ_g² 2σ_u² 1π_u⁴ 3σ_g² 1π_g².^[3] şeklinde yazılır.Buradaki 1π_g² terimi π* orbitalindeki iki elektronu temsil etmektedir. Hund kuralından dolayı bu elektronlar temel halde paralel spinlere sahip olmalıdır. Bundan dolayı dioksijen bir manyetik momente sahiptir.( yani dioksijen paramanyetiktir). Dioksijenin paramanyetik özelliğinin açıklanabilmesi moleküler orbital teorinin en büyük başarısıydı.

Çok atomlu moleküllerin elektron dizilimi herhangi bir fotonun emilimi ya da yayımı olmadan da değişebilir

Katılarda elektron dizilimi

Katılarda elektron durumları çok sayıda olabilir. Ayrık olmayı durdururlar ve olası durumların devamlı dizilerine karışırlar

Uygulamalar

Elektron diziliminin geniş ölçüde kullanıldığı alanlar organik ve inorganik kimyadır. Elektron dizilimi bazı basitleştirilmiş moleküler orbital teorilerin etkisinde kalarak değerlik elektron kavramını ortaya çıkardı. Değerlik elektronlar bir atomun kaç tane ve ne tipte bir kimyasal bileşik oluşturabileceğini belirleyen elektronlardır.

Bu yaklaşım kimyanın hesaplamayla ilgili alanı için dikkate alındı. Bu alan kimyasal özelliklere dair nicel tahminler yapmaya başladı. Bu hesaplamalar uzun yıllardan beri “atomik orbitallerin doğrusal kombinasyonları” yaklaşımına dayandırılarak yapıldı. Hesaplamaların son adımı moleküler orbitallerin Aufbau kuralı ile uyumlu olup olmadığını kontrol etmektir. 

Birden fazla elektrona sahip olan atomlar ve moleküller için elektron dizilimi hesaplanmak istendiğinde, elektronların hareketi de hesaba katılmalıdır. Bundan dolayı yapılmış bir hesaplama uzun süre kesin olamaz. Elektron diziliminin çok fazla olması, çoklu elektron sisteminin tanımlanmasını gerektirir. Ayrıca enerji tek bir dizilimle açıklanamaz. Fakat elektronik dalga fonksiyonu çok az sayıdaki elektron dizilimini açıklayabilmektedir. Bundan dolayı çoklu elektron dizilimleri için elektron dizilimi kavramı gerekli olmaya devam etmektedir.

Elektron diziliminin uygulandığı temel alanlardan biri emisyon spektrumlarıdır. Bu gibi durumlarda elektron dizilimini bir ya da birden fazla terim sembolü ile göstermek gereklidir. 

Notes

1. Miessler, G. L.; Tarr, D. A. (1999). Inorganic Chemistry (2nd bas.). Prentice-Hall. s. 38. 
2. Scerri, Eric R. (2007). The periodic table: its story and its significance. Oxford University Press. s. 239–240. ISBN 0-19-530573-6. https://books.google.com/?id=SNRdGWCGt1UC&pg=PA239. 
3. IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version:  (2006–) "configuration (electronic)".