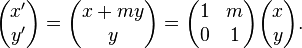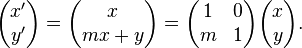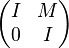Kesme haritalama

düzlem geometride ,bir 'kesme haritalama' bir doğrusal harita'nın sabit yönde her noktada yerinden olmasıdır.Orantılı bir miktarı ile işaretli mesafe'den bir çizgi bu yöne paralel dir .[1] Haritalamanın adlandırılması kesme dönüşümü,transveksiyon, ya da sadece kesmedir.
Bir örnek olarak herhangi bir noktadan gereken haritalama koordinatları 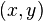 nin
nin 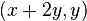 noktasınadir.Bu durumda yer değiştirme yataydır, sabit hat
noktasınadir.Bu durumda yer değiştirme yataydır, sabit hat 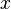 ekseni ve işaretli mesafe ise
ekseni ve işaretli mesafe ise 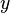 koordinatidir. Referans çizgisinin zıt kesimlerinde üzerindeki noktaların zıt yönlerde yer değiştirecegi unutulmamalidir.
kesme haritalamayı dönüş ile karıştırmamak gerekir.Düzlemin noktalarının bir kümesine uygulanacak bir kesme haritalamada bütün açı'lar arasında ( düz açılar hariç) değiklik olacak ve herhangi doğru parçası'nın uzunluğu yerdeğiştirme yönüne paralel değildir.Bu yüzden, genellikle, bir geometrik şekil diğer şekile deforme olacaktır.Örneğin kare içine kare olmayanlar paralelkenarlar ve çemberler içine elipsler dönebilir. Ancak bir kesici geometrik şekillerin korunması bölge , hizalama ve doğrudaş noktaların göreceli uzunluğunu korur.Bir kesme haritalama ile dikey haritalama arasındaki ana fark ve slanted (veya italik) harflerin stili gibidir.
koordinatidir. Referans çizgisinin zıt kesimlerinde üzerindeki noktaların zıt yönlerde yer değiştirecegi unutulmamalidir.
kesme haritalamayı dönüş ile karıştırmamak gerekir.Düzlemin noktalarının bir kümesine uygulanacak bir kesme haritalamada bütün açı'lar arasında ( düz açılar hariç) değiklik olacak ve herhangi doğru parçası'nın uzunluğu yerdeğiştirme yönüne paralel değildir.Bu yüzden, genellikle, bir geometrik şekil diğer şekile deforme olacaktır.Örneğin kare içine kare olmayanlar paralelkenarlar ve çemberler içine elipsler dönebilir. Ancak bir kesici geometrik şekillerin korunması bölge , hizalama ve doğrudaş noktaların göreceli uzunluğunu korur.Bir kesme haritalama ile dikey haritalama arasındaki ana fark ve slanted (veya italik) harflerin stili gibidir.
Üç boyutlu geometride de aynı tanım kullanılmıştır bunun dışında mesafe sabit bir düzlemde ölçülür.Üç boyutlu kesme dönüşümü katı figürlerin hacmini korur ama düzlem şekillerin alanlarını (yer değiştirme paralel olanlar hariç) değiştirir.Bu haritalama bir akışkan hareketi Couette akışıni tanımlar ve kesme zorlanması (yani deformasyon) adı bu nedenledir) altındaki katı malzeme'de parçacıkların bir yer değiştirmesi vardır. (bir sac'ın makaslar tarafından kesilmesiyle oluşur.)
Genel 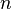 -boyutlu kartezyen uzay içinde (
-boyutlu kartezyen uzay içinde (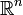 ) bu mesafe bir sabit hiperdüzlem yerdeğiştirmesinin yönüne paralel ölçülür. Bu geometrik dönüşüm bir
) bu mesafe bir sabit hiperdüzlem yerdeğiştirmesinin yönüne paralel ölçülür. Bu geometrik dönüşüm bir 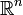 'nindoğrusal dönüşüm'üdür.Burada herhangi bir kümenin
'nindoğrusal dönüşüm'üdür.Burada herhangi bir kümenin 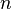 -boyut ölçüsü(hipervolüm) korunur.
-boyut ölçüsü(hipervolüm) korunur.
Tanım
Düzlemin yatay ve dikey makası

Düzlemde 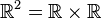 , bir yatay makas (veya paralel makas için x ekseni) koordinatları
, bir yatay makas (veya paralel makas için x ekseni) koordinatları 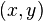
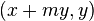 ;noktası ile genel bir nokta alan bir fonksiyondur;
;noktası ile genel bir nokta alan bir fonksiyondur;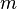 olarak adlandırılan sabit bir parametre, bir makas faktörüdür
Bu dönüşümlerin etkisi ile
olarak adlandırılan sabit bir parametre, bir makas faktörüdür
Bu dönüşümlerin etkisi ile 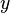 koordinat orantılı bir miktar yatay her noktada yerinden olmaktadır. Yukarıdaki herhangi bir noktada
koordinat orantılı bir miktar yatay her noktada yerinden olmaktadır. Yukarıdaki herhangi bir noktada 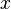 - eksenine yerinden olan doğru (artan
- eksenine yerinden olan doğru (artan 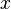 ) eğer
) eğer 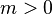 ve sola eğer
ve sola eğer 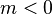 Ters yönde
Ters yönde 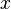 -ekseni hareket altında nokta, eksenindeki noktaları sabit kalıyor ise
-ekseni hareket altında nokta, eksenindeki noktaları sabit kalıyor ise
Paralel düz çizgiler 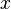 tüm diğer hatları da
tüm diğer hatları da 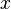 eksenli çapraz nokta hakkında, çeşitli açılardan tarafından, açık iken onlar, nerede olduğunuz ekseni kalır .
Dikey çizgiler, özellikle, olmak eğik ile çizgiler eğim
eksenli çapraz nokta hakkında, çeşitli açılardan tarafından, açık iken onlar, nerede olduğunuz ekseni kalır .
Dikey çizgiler, özellikle, olmak eğik ile çizgiler eğim 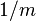 .
Bu nedenle makas faktörü
.
Bu nedenle makas faktörü 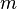 kotanjant açının
kotanjant açının 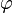 dikey çizgiler eğim,makas açısı olarak adlandırılan hangi.
dikey çizgiler eğim,makas açısı olarak adlandırılan hangi.
Bir noktanın koordinatları eğerbir sütun vektör olarak yazılırsa(bir 2×1 matris),bir 2×2 matrisile çarpımı olarak makas haritalama yazılabilir:
A dikey makası (veya 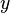 -axis)ya benzer hattın paralel makası ,
-axis)ya benzer hattın paralel makası , 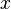 'ın ve
'ın ve 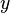 'ın rolu dışında yerlerini değiştirdiler.O transpoze matris ile koordinat vektörleri çarpmaya karşılık gelir:
'ın rolu dışında yerlerini değiştirdiler.O transpoze matris ile koordinat vektörleri çarpmaya karşılık gelir:
Genel kesme haritalaması
vektor uzayı V ve altuzay W için, bir kesme sabiti Wdir.Wye çevrilen bütün paralel vektörlerin çevirisi.
Daha net olmak gerekirse, Eğer V Wdir ve W′nin doğrudan toplamı dır , ve
bizim vektörler
- v = w + w′
buna uygun olarak, tipik sabitleme W Ldir burada
- L(v) = (w + Mw′) + w ′
burada M bir doğrusal haritalamadır W′ den W içinedir. Therefore in blok matris terms L can be represented as
Köşegen bloklarla I (birim matris), ile M köşegen üzerinde, ve 0 altında.
Uygulamalar
Makas haritalama aşağıdaki uygulamalar William Kingdon Clifford tarafından not edilmiştir. "Makaslar birbiri ardına bize eşit alan bir üçgen için düz çizgiler ile sınırlı herhangi bir şekle azaltmak için olanak sağlayacak" "... bir dik açılı üçgen içine makas bir üçgen olabilir ve bu kendi alanında değiştirmez. Böylelikle, herhangi bir üçgenin alanı, aynı baz ve ters açıdan bazında dik eşit yükseklikte olan dikdörtgen yarısı alandır"[2] Bir kesme haritalamanın alan koruyucu özelliği alanı ile ilgili sonuçlar için kullanılabilir. Örneğin, Pisagor teoremi makas haritalama ile gösterilmiştir.[3] Bir keyfi bir açı ile dijital görüntü döndürmek için üç makas eşleştirmeleri (sonra tekrar yatay, dikey, yatay)nedeniyle bir algoritmik bir dizi kullanan Alan W. Paethtir.Her adımda piksel bir anda yalnızca bir sütun veya bir satır işler yana algoritması, uygulamak için çok basit ve çok verimli.[4]
Kaynakça
- ↑ Definition according to Weisstein, Eric W. Shear From MathWorld − A Wolfram Web Resource
- ↑ William Kingdon Clifford (1885) Common Sense and the Exact Sciences, page 113
- ↑ Mike May S.J. Pythagorean theorem by shear mapping, from Saint Louis University; requires Java and Geogebra. Click on the "Steps" slider and observe shears at steps 5 and 6.
- ↑ Alan Paeth (1986), A Fast Algorithm for General Raster Rotation. Proceedings of Graphics Interface '86, pages 77–81.
- Weisstein, Eric W. "Shear" from Mathworld, A Wolfram Web Resource.