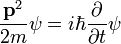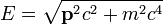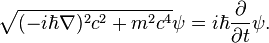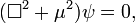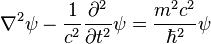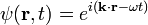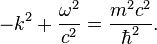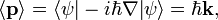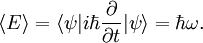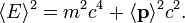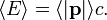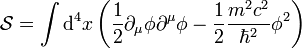Klein-Gordon denklemi

Klein-Gordon Denklemi, (bazı kaynaklarda Klein-Fock-Gordon Eşitliği olarak da ifade edilir) Schrödinger denkleminin bağıl/göreli (relativistik) olan versiyonudur ve atomaltı fizikte kendi ekseni etrafında dönmeyen parçacıkları tanımlamada kullanılır. Oskar Klein ve Walter Gordon tarafından bulunmuştur.

Matematiksel Açılım

Serbest bir parçacık için Schrödinger denklemi aşağıdaki gibidir.

$\frac{\mathbf{p}^2}{2m} \psi = i \hbar \frac{\partial}{\partial t}\psi$

burada

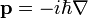$\mathbf{p} = -i \hbar \mathbf{\nabla}$ momentum operatörü, 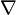$\nabla$ ise del operatörüdür.

Schrödinger denklemi Einstein'ın Özel Görelilik Kuramı'nı hesaba katmadığı için özellikle atomaltı parçacık hesaplamalarında yetersiz kalır.

Özel Görelilik Kuramı'ndan enerjinin tanımını ihraç edip

$E = \sqrt{\mathbf{p}^2 c^2 + m^2 c^4}$

sonra, bu formüle kuvantum mekanik momentum operatörünü eklediğimizde,

$\sqrt{(-i\hbar\mathbf{\nabla})^2 c^2 + m^2 c^4} \psi= i \hbar \frac{\partial}{\partial t}\psi.$

sonucunu alırız. Ancak bu eşitlik karekökten dolayı gayrilokal ve düzensiz bir yapıdadır ve bu yüzden Klein ve Gordon eşitliğin daha objektif bir versiyonunu tümdengelmişlerdir.

$(\Box^2 + \mu^2) \psi = 0,$

burada

$\mu = \frac{mc}{\hbar} \,$

ve

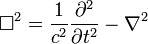$\Box^2 = \frac{1}{c^2}\frac{\partial^2}{\partial t^2} - \nabla^2\,$ olur.

Bu yeni operatöre d'Alembert operatörü denir ve günümüzde skaler (sıfır rotasyonlu) parçacıklar için alan denklemi olarak kullanılmaktadır.

Göreli serbest parçacık çözümü

Serbest bir parçacığın Klein-Gordon denklemi aşağıdaki gibi yazılabilir.

$\mathbf{\nabla}^2\psi-\frac{1}{c^2}\frac{\partial^2}{\partial t^2}\psi = \frac{m^2c^2}{\hbar^2}\psi$

Yukarıdaki ifadenin gayrigöreli versiyonu ise bu şekilde ifade edilebilir:

$\psi(\mathbf{r}, t) = e^{i(\mathbf{k}\cdot\mathbf{r}-\omega t)}$

Ancak elbette bu durumda,

$-k^2+\frac{\omega^2}{c^2}=\frac{m^2c^2}{\hbar^2}.$

engeli oluşacaktır. Gayrigöreli parcçacıklarda olduğu gibi, aynı ifadenin enerji ve momentum için olan versiyonları,

$\langle\mathbf{p}\rangle=\langle \psi |-i\hbar\mathbf{\nabla}|\psi\rangle = \hbar\mathbf{k},$

ve

$\langle E\rangle=\langle \psi |i\hbar\frac{\partial}{\partial t}|\psi\rangle = \hbar\omega.$

şeklinde formüle edilir. Bu noktada eşitliği k ve ω bilinmeyenleri için çözüp yukarıda değindiğimiz engel denklemine ihraç ettiğimizde m>0 kütleli parçacıkların enerji ve momentum değerleri arasındaki bağlantıyı formüle etmiş oluruz.

$\left.\right. \langle E \rangle^2=m^2c^4+\langle \mathbf{p} \rangle^2c^2.$

Kütlesiz parçacıklar için, yukarıdaki denklemde m`i 0 olarak alabiliriz. Bu durumda kütlesiz parçacığın enerji ve momentumu arasında,

$\left.\right. \langle E \rangle=\langle |\mathbf{p}| \rangle c.$

ilişkisine ulaşırız.

Aksiyom

Klein-Gordon denklemi aşağıdaki aksiyom kullanılarak tümdengelinebilir.

$\mathcal{S}=\int \mathrm{d}^4x \left(\frac{1}{2}\partial_{\mu}\phi \partial^{\mu}\phi - \frac{1}{2}\frac{m^2 c^2}{\hbar^2} \phi^2 \right)$

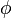burada $\phi$ Klein-Gordon alanını, 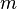$m$ ise kütleyi ifade etmektedir.

Ayrıca bakınız

• Dirac denklemi
• Kuantum alan kuramı
• Skalar alan
• Schrödinger denklemi
• Klein-Gordon denkleminin matematiksel argümanları bu sayfada tartışılmıştı: Dispersive PDE Wiki.

Dış bağlantılar

• Lineer Klein-Gordon Denklemi at EqWorld: Matematik Denklemleri Dünyasi, Rusya.
• Gayri-Lineer Klein-Gordon Denklemi at EqWorld: Matematik Denklemleri Dünyasi, Rusya.
• Klein-Gordon denkleminin genellemesi ABD