Lagrange çarpanı

Resim 1: Kırmızı renkle gösterilen g(x, y) = c fonksiyonu kısıtlaması altında, f(x, y) 'nin enbüyük değerini bulmak için x ve y bulunuz.

Resim 2: Resim 1'in üstten çizilmiş hali. Kırmızı çizgi g(x, y) = c kısıtlamasını göstermekte ve mavilerde f(x, y)'nın hatlarını göstermektedir. Kırmızı çizginin teğetsel bir şekilde mavi hatlarına dokunduğu kısım aradığımız çözümdür. d₁ > d₂ olduğundan dolayı, çözüm, kırmızı çizginin mavi halkaya teğet olduğu nokta, f(x, y) fonksiyonunun enbüyük değerini verir.

Optimizasyon yaparken, Lagrange çarpanı methodu (Joseph Louis Lagrange^[1]'dan sonra isimlendirildi), bir fonksiyonun maksimum ve minimum noktalarını bulmak için kullanılan bir yöntemdir.

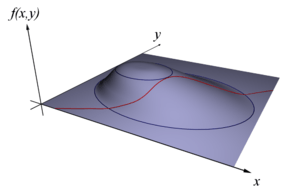
Örnek olarak, (bkz. resim 1), optimizasyon problemine bakarsak;

g(x, y) = c denklemi ile sınırlandırılmış

f(x, y) işlevinin (fonksiyonunun) enbüyük değeri.

Burada f ve g fonksiyonlarının ilk kısmi türevilerinin devamlı olması gerekmektedir. Lagrange çarpanı diye isimlendirdiğimiz yeni bir değişken tanımlıyoruz (λ), ve lagrange işlevimiz aşağıdaki şekilde tanımlanıyor;

${\displaystyle \Lambda (x,y,\lambda )=f(x,y)+\lambda \cdot {\Big (}g(x,y)-c{\Big )},}$

burada işleve λ çıkarabilir de eklenebilir de, iki durumda da aynı sonuç elde edilebilir. Eğer f(x₀, y₀) orijinal sınırlandırılmış problemde f(x, y)'nin maksimum noktasıysa, öyle bir λ₀ noktası olacaktır ki ve (x₀, lagrange fonksiyonu için y₀, λ₀) durgun nokta olur (durgun noktalar, Λ fonksiyonunun ilk kısmi türevinin sıfır olduğu noktalardır.). Gelgelelim, original problemin her sabit nokta için bir çözümü olmayabilir. Lagrange methodu, sınırlandırılmış problemde optimizasyon yapabilmek için gerekli işlevi elde etmemizi sağlar.^{[2][3][4][5][6]} Ayrıca, gerekli koşullar, en küçük (minimum) ve en büyük (maksimum) noktalar için vardır.

Giriş

Calculustaki en popüler problemlerden biri, bir fonksiyonun maksimumunu veya minimumunu bulmaktır ama genellikle zordur, kapalı bir yapı bulmak karışık fonksiyonlar için. Ne zaman bir fonksiyonu mümkün olduğunca küçük veya büyük yapmaya çalıştığımızda karşılaşabiliriz. Lagrange çarpanı methodu güçlü bir araçtır, bu tarz problemleri, açıkça çözme gereksinimi olmadan çözer ve fazladan değişkenleri yok etmek için kullanır.

Aşağıda tanıtılan iki boyutlu problemi ele alalım:

en büyük olan f(x, y)

bağımlı olan g(x, y) = c

Sezgisel olarak lagrange çarpanını, maksimum noktasında, f(x, y) fonksiyonu, g = c bu fonksiyonun komşu noklarının yönünde artamaması gerektiğidir. Eğer artıyorsa, g = c yönünde daha büyük bir değere gidilebilir, bu başlangıç noktası aslında maksimum noktası değil demektir.

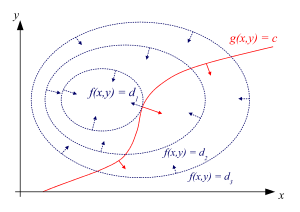
Bir fonksiyonun eşyükselti eğrileri gözümüşde canlandırabiliriz. Örnek olarak bir f fonksiyonu için f(x, y) = d herhangi bir d değeri için, ve eşlik yükselti eğrisi için g(x, y) = c şeklinde yazılabilir.

Farz edelim g=c hattı üstünde yürüdük. f'nin biz yürüdükçe değişmeyen noktalarını bulmak istiyoruz, çünkü bu noktalar maxima olabilirler. İki bu durum oluşabilir; İlki, biz f hattını takip ediyorsak, çünkü f tanımı gereği, f değişmeyecektir biz onun hattının bulunduğu çizgide yürüdükçe ve bu da f ve gnin yükselti çizgilerinin paralel olduğunu gösterir. İkici olası durum da, fnin yönünün değişmediği bir noktaya ulaştığımız durumlarda ortaya çıkar.

İlk olası durumu ele alırsak, kontrol etmek için, fonksiyonun gradyanı yükselti çizgisine dik olduğundan dolayı, f ve gnin yükselti eğrileri paralel olurlar, sadece ve sadece f ve gnin gradyanı paralel ise. Böylelikle biz öyle (x,y) noktaları istiyoruzki g(x,y)=c olsun ve

${\displaystyle \nabla _{x,y}f=-\lambda \nabla _{x,y}g}$,

herhangi bir λ için

${\displaystyle \nabla _{x,y}f=\left({\frac {\partial f}{\partial x}},{\frac {\partial f}{\partial y}}\right),\qquad \nabla _{x,y}g=\left({\frac {\partial g}{\partial x}},{\frac {\partial g}{\partial y}}\right).}$

ayrı ayrı gradyanlardır. Sabit olan λ gereklidir, çünkü iki gradyan vektörleri paralel olduğu halde, gradyan vektörlerinin büyüklükleri genellikle eşit olmazlar ve eksi işareti geleneksellikten geliyor. Aynı zamanda, bu sabit Lagrange çarpanı diye adlandırılmıştır.

Bu method aynı zamanda ikici olası durumuda çözüyor: eğer f herhangi bir yönde değişmiyorsa onun gradyanı sıfırdır ve Lagrange çarpanını sıfır seçerek çözüme ulaşabiliriz g bağımsız bir şekilde.

Bu koşulları tek bir denklemde birleştirmek için, yardımcı bir fonksiyon tanıtacağız,

${\displaystyle \Lambda (x,y,\lambda )=f(x,y)+\lambda \cdot {\Big (}g(x,y)-c{\Big )},}$

ve

${\displaystyle \nabla _{x,y,\lambda }\Lambda (x,y,\lambda )=0.}$

'nin için çözeceğiz.

Bu Lagrange çarpanının methodudur. Dikkate alın ki ${\displaystyle \nabla _{\lambda }\Lambda (x,y,\lambda )=0}$, g(x, y) = c demektir.

f'nin zoraki oluşturulmuş uç noktası Lagrangian Λnın kritik noktalarıdır, ama Λnın lokal uç noktaları değildir.

Lagrangian, Hamiltonian olarak yeniden düzenlenebilir ve bu durumda çözümler lokal minimadır Hamiltonian için. Optimal kontrol teorisinde bu yapılmıştır, Pontryagin's minimum prensibi formunda.

Lagrangian'nın çözümlerinin extrema olması şart olmadığından dolayı zorluklar ortaya çıkarmaktadır, sayısal optimizasyonlar için. Bunlar gradyanın büyüklüğünü hesaplayarak belirlenebilir.

1. Mécanique Analytique sect. IV, 2 vols. Paris, 1811 https://archive.org/details/mcaniqueanalyt01lagr
2. Bertsekas, Dimitri P. (1999). Nonlinear Programming (Second bas.). Cambridge, MA.: Athena Scientific. ISBN 1-886529-00-0. 
3. Vapnyarskii, I.B. (2001), "Lagrange multipliers", Hazewinkel, Michiel, Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104, http://eom.springer.de/Lagrange_multipliers.htm .
4. • Lasdon, Leon S. (1970). Optimization theory for large systems. Macmillan series in operations research. New York: The Macmillan Company. s. xi+523. MR 337317. 
   • Lasdon, Leon S. (2002). Optimization theory for large systems (reprint of the 1970 Macmillan bas.). Mineola, New York: Dover Publications, Inc.. s. xiii+523. MR 1888251. 
5. Hiriart-Urruty, Jean-Baptiste; Lemaréchal, Claude (1993). "XII Abstract duality for practitioners". Convex analysis and minimization algorithms, Volume II: Advanced theory and bundle methods. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences]. 306. Berlin: Springer-Verlag. s. 136–193 (and Bibliographical comments on pp. 334–335). ISBN 3-540-56852-2. MR 1295240. 
6. Lemaréchal, Claude (2001). "Lagrangian relaxation". Michael Jünger and Denis Naddef. Computational combinatorial optimization: Papers from the Spring School held in Schloß Dagstuhl, May 15–19, 2000. Lecture Notes in Computer Science. 2241. Berlin: Springer-Verlag. s. 112–156. DOI:10.1007/3-540-45586-8_4. ISBN 3-540-42877-1. MR 1900016.