Paralelkenar yasası

Bir paralelkenar üzerinde kenarlar mavi, köşegenler ise kırmızı ile gösterilmiştir

Matematikte paralelkenar yasasının en temel formu(ayrıca paralelkenar özdeşliği denir), temel geometriye aittir. Yasa, paralelkenarın tüm kenarlarının karelerinin toplamının köşegenlerinin karelerinin toplamına eşit olduğunu söyler. Yandaki gösterimdeki paralelkenarın kenarları; (AB), (BC), (CD) ve (DA). Öklidci geometriden beri, paralelkenarın karşılıklı kenarları mutlaka eşit olmalıdır.(AB) = (CD) ve (BC) = (DA)

Yasa şu şekilde ifade edilebilir,

${\displaystyle 2(AB)^{2}+2(BC)^{2}=(AC)^{2}+(BD)^{2}\,}$

Paralel kenarın dikdörtgen olması durumunda ise köşegenler eşit olmalıdır (AC) = (BD) yani,

${\displaystyle 2(AB)^{2}+2(BC)^{2}=2(AC)^{2}\,}$

İfade, dört kenarı eşit olmayan genel dörtgenler içinse Pisagor teoremine indirgenebilir,

${\displaystyle (AB)^{2}+(BC)^{2}+(CD)^{2}+(DA)^{2}=(AC)^{2}+(BD)^{2}+4x^{2}.\,}$

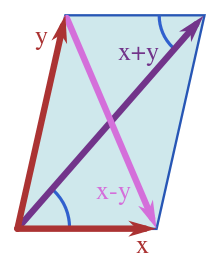
burada x köşegenlerinin orta noktasını birleştiren çizginin uzunluğudur. Şemada görüldüğü gibi, paralelkenar için x = 0 ve genel formül paralelkenar yasasındakine eşdeğerdir.

iç çarpım uzayları içinde paralelkenar kanunu

paralelkenar kanunu içinde ilgili vektörler.

Bir normlu uzayı içinde paralelkenar kanununun durumu normlarla ilişkili bir denklemdir:

${\displaystyle 2\|x\|^{2}+2\|y\|^{2}=\|x+y\|^{2}+\|x-y\|^{2}.\,}$

Bir iç çarpım uzayı içinde,norm iç çarpım kullanımı belirleniyor:

${\displaystyle \|x\|^{2}=\langle x,x\rangle .\,}$

Tanımın bir sonucu olarak,bir iç çarpımlı uzay içinde parallelkenar kanunu bir cebrik özdeşliktir,iç çarpımın özellikleri kullanılarak kolayca kurulmuştur:

${\displaystyle \|x+y\|^{2}=\langle x+y,x+y\rangle =\langle x,x\rangle +\langle x,y\rangle +\langle y,x\rangle +\langle y,y\rangle ,\,}$

${\displaystyle \|x-y\|^{2}=\langle x-y,x-y\rangle =\langle x,x\rangle -\langle x,y\rangle -\langle y,x\rangle +\langle y,y\rangle .\,}$

bu iki bağıntı ekleniyor:

${\displaystyle \|x+y\|^{2}+\|x-y\|^{2}=2\langle x,x\rangle +2\langle y,y\rangle =2\|x\|^{2}+2\|y\|^{2},\,}$

olarak gereklidir.

Eğer x yye ortogonal ise, ${\displaystyle \langle x,\ y\rangle =0}$ ve alınan bir toplamın normu için yukardaki denklem :

${\displaystyle \|x+y\|^{2}=\langle x,x\rangle +\langle x,y\rangle +\langle y,x\rangle +\langle y,y\rangle =\|x\|^{2}+\|y\|^{2},}$

Bu pisagor teoremidir.

Normlu vektör uzaylarını paralelkenar kanunu karşılar

En gerçek ve karmaşık normlu vektör uzayları iç çarpımlı değildir, ama tüm normlu vektör uzaylarının normları var (tanımı ile).Örneğin, bir ortak kullanılan norm p-normdur:

${\displaystyle \|x\|_{p}=\left(\sum _{i=1}^{n}|x_{i}|^{p}\right)^{1/p},}$

$x_i$ burada ${\displaystyle x}$ vektörünün bileşenleridir.

Verilen bir norm,yukarda paralelkenar kanununun iki tarafını teke evriltilebilir.Dikkat çekici gerçektir şudur ki paralelkenar kanunu tutarlı ise, o zaman standart bir iç çarpım, alışılmış bir yolla ortaya çıkmalıdır. Özel olarak, bu p-norm'un ancak ve ancak p = 2,Öklidyen norm veya standard norm gibi-adlandırılması uygundur.^[1][2]

Herhangi norm için paralelkenar kanunu karşılar (bu zorunlu olarak bir iç çarpım normudur), iç çarpım üreten norm polarizasyon özdeşliğinin bir sonucu olarak tekliktir.Gerçek durum içinde,polarizasyon özdeşliği ile veriliyor:

${\displaystyle \langle x,y\rangle ={\|x+y\|^{2}-\|x-y\|^{2} \over 4},\,}$

veya, eşdeğerliği, ile:

${\displaystyle {\|x+y\|^{2}-\|x\|^{2}-\|y\|^{2} \over 2}{\text{ veya }}{\|x\|^{2}+\|y\|^{2}-\|x-y\|^{2} \over 2}.\,}$

karmaşık durum içinde aşağıdaki ile veriliyor:

${\displaystyle \langle x,y\rangle ={\|x+y\|^{2}-\|x-y\|^{2} \over 4}+i{\|ix-y\|^{2}-\|ix+y\|^{2} \over 4}.}$

Örneğin, p-norm ile p = 2 ve gerçel vektörler ${\displaystyle x,\ y\,}$ kullanılıyor, iç çarpımın evirtimi için süreç aşağıdadır:

${\displaystyle {\begin{aligned}\langle x,y\rangle &={\|x+y\|^{2}-\|x-y\|^{2} \over 4}\\&={\frac {1}{4}}\left[\sum |x_{i}+y_{i}|^{2}-\sum |x_{i}-y_{i}|^{2}\right]\\&={\frac {1}{4}}\left[4\sum x_{i}y_{i}\right]\\&=(x\cdot y),\end{aligned}}}$

bu iki vektörlerin standard nokta çarpımıdır.

Notlar ve iç-hat kaynakları

1. Cyrus D. Cantrell (2000). Modern mathematical methods for physicists and engineers. Cambridge University Press. s. 535. ISBN 0-521-59827-3. http://books.google.com/books?id=QKsiFdOvcwsC&pg=PA535. "if p ≠ 2, there is no inner product such that ${\displaystyle {\sqrt {\langle x,\ x\rangle }}=\|x\|_{p}}$ because the p-norm violates the parallelogram law." 
2. Karen Saxe (2002). Beginning functional analysis. Springer. s. 10. ISBN 0-387-95224-1. http://books.google.com/books?id=0LeWJ74j8GQC&pg=PA10. 

Ayrıca bakınız

• Apollonius' teoremi
• Birleşmeliözellikler
• Polarizasyon özdeşliği

Dış bağlantılar

• The Parallelogram Law Proven Simply at Dreamshire blog
• The Parallelogram Law: A Proof Without Words at cut-the-knot
• Proof of Parallelogram Law at Planet Math
• A generalization of the "Parallelogram Law/Identity" to a Parallelo-hexagon and to 2n-gons in General - Relations between the sides and diagonals of 2n-gons (Douglas' Theorem) at Dynamic Geometry Sketches, an interactive dynamic geometry sketch.