Pound-Drever-Hall tekniği

Pound-Drever-Hall tekniği, optik kovuk'a veya buhar hücresine kilitleme yapılarak lazer frekansı sabitleme yöntemlerinden biridir. İnterferometresel gravitasyonel dalga ölçerlerin temel teknolojisini oluşturur. Bunun yanında atom fiziği ve zaman ölçüm standartlarında oldukça sık rastlanır. Pound-Drever-Hall tekniğinin (PDH) kavramsal temelleri frekans modülasyonu ile yakından alakalıdır. Birini anladığınız zaman diğerini halletmek kolay olur. PDH tekniğinin basit arka planı prensipte şudur: Lazer frekansı Fabry-Perot interferometresi yardımıyla ölçülür ardından bu ölçüm lazeri besleyerek frekans dalgalanmasını bastırır.

Lazer sabitleme

Son yıllarda Pound-Drever-Hall tekniği lazer frekans sabitlemesinin bir dayanak noktası hâline gelmiştir. Bütün lazerler belli bir seviyede frekans sapması gösterdiği için frekans sabitlemesi yüksek hassasiyet için gereklidir. Bu sabitsizliğe öncelikle lazer oyuk uzunluğunu, lazer sürücü akımını ve gerilim dalgalanmasını, atomik geçiş genişliğini değiştiren sıcaklık değişimleri, mekaniksel hatalar ve lazer kazanç dinamiği ve daha bir sürü etken neden olur. PDH kilitmesi sabit referans oyuğunun rezonans şartına denk gelmesi için lazeri aktif şekilde ayarlayarak bu probleme makul bir çözüm sunar.

PDH sabitlemesinden elde edilen nihai çizgi-genişliği bir sürü etkene bağlıdır. Sinyal tahlili nokta-ı nazarından, kilitleyen sinyal üzerindeki gürültü hiçbir zaman pozlanan şat gürültüsü limitinden daha yüksek olamaz. Bununla birlikte, bu kısıtlama lazerin oyuğu takip edebilmesi için ne kadar yakın yapıldığını gösterir. Sıkı kilitleme şartları için, çizgi-genişliği termal gürültü tarafından dayatılan limitlere kadar ulaşabilen optik oyuğun mutlak sabitliğine bağlıdır. PDH tekniğini kullanarak 40 mHz altında optik çizgi-genişlikleri kanıtlanmıştır.

Uygulama alanları

Belirgin olarak,interferometresel gravitasyonel dalga saptama alanı ciddi olarak, optiksel oyuklar tarafından sağlanan yüksek hassasiyete bağlıdır.PDH tekniği, ferdi kuantum durumlarının dar spektoskopik derinlikleri gerektiğinde de kullanılır,atom fiziği, zaman ölçüm standartları ve kuantum bilgisayarlarında olduğu gibi.

Tekniğe genel bir bakış

Lazer frekansının Fabry-Perot oyuğuna kilitlenmesi için PDH servo döngüsünün şeması.Lazerden gelen ışık faz modülatörüne gönderilir ve ardından oyuk üzerine yöneltilir.(Diyot lazerler için,hızlı frekans veya faz modülasyonu, ekstra bir elektro-optik veya akusto-optik modulatöre gerek kalmaksızın sadece diyot akımını modüle ederek gerçekleştirilebilir.) Yalıtıcı(isolator) PDH düzeneğine dahil değildir, o sadece muhtelif optiksel parçalardan yansıyan ışığın lazerin içine geri yansımamasını sağlar.Polarize ışın ayracı ve λ/4 plaka ışığın iki yönde işleyişini ayırt etmek için birlikte çalışır; 1→2 yönünde işleyen ışık doğrudan geçer ve oyuğa girerken, 2→1 yönünde işleyen ışık ise optiksel oyuktan fotosele doğru yönlendirilir. Faz modülatörü osilatörden gelen sinüs dalgası ile güdülür; bu, yanbandları lazer ışığı üzerine bastırır. PDH okunan-veri fonksiyonu bölümünde de ifade edildiği gibi fotoselin sinyali(karıştırıcı ve düşük geçirgen filtreden geçen) lazerin frekansını kontrol eden aksamını geri besleyen bir hata sinyali üretmek için tersten module edilir (demodulation).

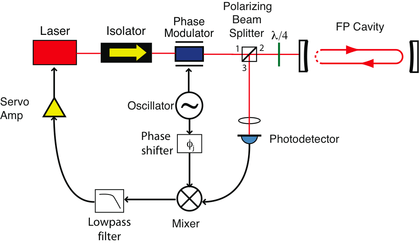
Bir taşıyıcı frekans ve iki yan band içeren fazı modüle edilmiş bir ışık iki aynalı oyuğun üzerine yöneltilir.Kapalı oyuktan yansıyan ışık yüksek hızlı fotodedektör kullanılarak ölçülür,

yansıyan sinyal değiştirilmemiş iki tane yan band ile birlikte bir tane fazı kaymış taşıyıcı bileşikten oluşur. Işık modülasyonu ile aynı fazda olan yerel bir osilatör ile fotodedektörün sinyali karıştırılır. Faz kayması ve filtrelemeden sonra, sonuçlanan elektronik sinyal lazer taşıyıcısı ile optiksel oyuğun rezonansa ne kadar yakın olduğu hakkında ölçü verir ve belki aktif lazer sabitlemesi için geri besleme olarak kullanılır. Geri besleme umumiyetele, hata sinyal verisini alan ve bunu lazeri geri besleyebilen optiksel oyuğun rezonansı ile kilitli kalması için gerilime dönüştüren PID denetleyicisi kullanılarak yapılır.

PDH okunan-veri fonksiyonu

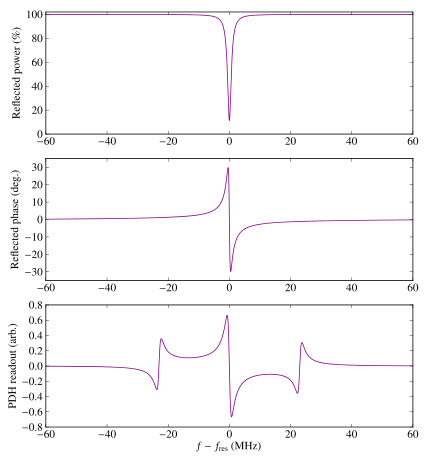
PDH okunan-veri fonksiyonu bir oyuğun rezonans şartı için bir ölçü verir.Oyuğun transfer fonksiyonunun(simetrik ve çifttir) frekansa göre türevini alarak bu, frekansın bir tek fonksiyonudur ve bundan dolayı sadace lazerin çıkış frekansı ω ve oyuğun rezonans frekansı ω_res arasında denksizlik olup olmadığını göstermekle kalmaz ve fakat ω'nın ω_res 'dan daha büyük veya küçük olduğunu da gösterir.Okunan-veri fonsiyonunun sıfır kesiti sadece oyuğun içersindeki ışığın frekansından kaynaklanan ışık şiddeti dalgalanmasına duyarlıdır ve lazerin kendisinden olan şiddet dalgalanmasına ise duyarsızdır.

Matematiksel olarak ışığın frekansı f=ω/2π elektrik alanınıyla E₀e^iωt temsil edilebilir.Eğer ışığın fazı βsin(ω_mt) tarafından modüle edilmiş ise ortaya çıkan alan şöyledir

$\begin{align} E_{\text{i}} &= E_0 e^{i( \omega t+\beta\sin(\omega_\mathrm{m} t))} \\ &\approx E_0 e^{i\omega t} [1+i \beta \sin(\omega_\mathrm{m} t)] \\ &= E_0 e^{i \omega t}\left[1+\frac{\beta}{2}e^{i\omega_\mathrm{m} t}-\frac{\beta}{2}e^{-i \omega_\mathrm{m} t}\right]. \end{align}$

Bu alana üç bileşenin süperpozisyonu olarak bakılabilir. Birinci bileşen açısal frekans ω'nın elektrik alanıdır,taşıyıcı olarak bilinir, ve sırasıyla ikinci ve üçüncü bileşenlere ω+ω_m ve ω-ω_m ise yanbandlar denilir.

Genelde,iki aynalı bir Fabry-Perot oyuğudan yansıyan ışık E_r,oyuğun üzerine gelen ışık E_i ile müteakip transfer fonksiyonu ile bağlıdır.

$R(\omega)=\frac{E_{\text{r}}}{E_{\text{i}}}=\frac{-r_1+(r_1^2+t_1^2)r_2e^{i2\alpha}}{1-r_1r_2e^{i2\alpha}},$

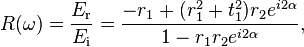
burada α=ωL/c dir ve r₁ ve r₂ ise oyuğun 1 ve 2 nolu aynalarının yansıtma katsayılarıdır ve t₁ ve t₂ ise aynaların iletme katsayılarıdır.

Bu transfer fonksiyonunu fazı modüle edilmiş ışık E_i' e uygularsak yansıyan ışık E_r'ı verir.^{[not 1]}

$E_{\text{r}}=E_0\left[R(\omega)e^{i\omega t}+R(\omega+\omega_\mathrm{m})\frac{\beta}{2}e^{i(\omega+\omega_\mathrm{m})t}-R(\omega-\omega_\mathrm{m})\frac{\beta}{2}e^{i(\omega-\omega_\mathrm{m})t}\right].$

Yansıyan ışığın gücü P_r elektrik alanın karesinin büyüklüğü E_r ^*E_r ile orantılıdır, bazı cebirsel manipülasyonlardan sonra şöyle gösterilebilir;

$\begin{align} P_{\text{r}} =&\ P_0\left|R(\omega)\right|^2+P_0\frac{\beta^2}{4}\Big\{\left|R(\omega+\omega_\mathrm{m})\right|^2+\left|R(\omega-\omega_\mathrm{m})\right|^2\Big\} \\ &+ P_0\beta\Big\{\textrm{Re}[\chi(\omega)]\cos{\omega_\mathrm{m} t} + \textrm{Im}[\chi(\omega)]\sin{\omega_\mathrm{m} t}\Big\} + (\text{terms in } 2\omega_\mathrm{m}). \end{align}$

Burada, P₀∝|E₀|² Fabry-Perot oyuğunun üzerine gelen ışığın gücüdür ve χ şöyle tanımlanır;

$\chi(\omega) = R(\omega)R^*(\omega+\omega_\mathrm{m})-R^*(\omega)R(\omega-\omega_\mathrm{m}) .$

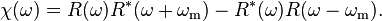
Bu χ alakamızın nihai niceliğidir; ve ω-ω_res 'ın antisimetrik bir fonksiyonudur.P_r'dan tersten modüle edilerek çıkartılabilir.Evvela, yansıyan ışık, P_r ile orantılı olan V_r gerilimi üreten fotodiyot üzerine yöneltilir. Sonra, bu gerilim V^'_r ı üretmek için orijinal modüle geriliminin gecikmiş faz versiyonu ile karıştırılır.

$\begin{align} V_{\text{r}}' &= V_{\text{r}}\cos(\omega_\mathrm{m} t+\varphi) \propto P_{\text{r}}\cos(\omega_\mathrm{m} t + \varphi). \\ \end{align}$

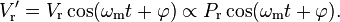
Son olarak, V′_r herhangi sinüssel salınan terimleri kaldırmak için düşük geçirgen filtreye doğru gönderilir. Karışımın ve düşük geçirgen filtrenin ürettiği gerilim V' nin sadece χ'ı içeren terimlerini ihtiva ettiği bu birleşim;

$V(\omega) \propto \textrm{Re}[\chi(\omega)] \cos\varphi + \textrm{Im}[\chi(\omega)]\sin\varphi.$

Teoride(nazariyyede), χ, biri φ=0 ve diğeri φ=π/2 olmak üzere iki tersten modüle yollarının kurulmasıyla tamamen çıkartılabilir.Pratikte ise ω_m' nin makul seçeneği ile χ'i neredeyse tamamen reel veya sanal yapmak mümkündür ve böylece sadece bir tersten modüle yolu zaruridir.V(ω) ile birlikte uygun seçilen φ, PDH okunan-veri sinyalidir.

Notlar

1. _{Transfer fonksiyonu R üstsel terimlerin her birine bağımsız olarak uygulanır çünkü Fabry-Perot oyuğu değişkensiz-zamanlı sistemdir. Oyuğun ışığın frekansı ω1'a cevabı aynı anda cavap veren frekansı ω2 olan başka bir ışığa da kayıtsız olarak aynıdır.}

Kaynakça

1. Black, Eric D. (2001). "An introduction to Pound–Drever–Hall laser frequency stabilization" (PDF). Am J Phys 69 (1): 79. doi:10.1119/1.1286663
2. Drever, R. W. P., Hall, J. L., Kowalski, F. V., Hough, J., Ford, G. M., Munley, A. J. H. Ward (1983). "Laser phase and frequency stabilization using an optical resonator". Appl Phys B 31 (2): 97. doi:10.1007/BF00702605
3. Black, Eric. "Notes on the Pound-Drever-Hall technique" (PDF). LIGO Technical Note. Retrieved 21 June 2014.
4. Ghatak, Ajoy Kumar (Jul 20, 1989). Optical Electronics. New York: Cambridge University Press. p. 254. ISBN 0521306434.
5. "[Http://stablelasers.com/spec-sheets/SLS Cavity comparisons 1.pdf Comments on different cavity geometries: notched horizontal, vertical midplane and spherical]" (PDF). http://stablelasers.com. Stable Lasers. Retrieved 9 April 2014.
6. Kessler T et al. (2014). "A sub-40-mHz-linewidth laser based on a silicon single-crystal optical cavity". Nature Photonics 6: 687–692. doi:10.1038/nphoton.2012.217.
7. Abramovici A et al. (1992). "LIGO: The Laser Interferometer Gravitational-Wave Observatory". Science 256 (5055): 325–333. doi:10.1126/science.256.5055.325. PMID 17743108.