Süper kütle çekimi
Kuramsal fizikte, süper kütle çekimi genel görelilik kuramı ve süper simetriyi birleştiren bir alan kuramıdır.Süper kütleçekiminde, süper simetri bölgesel simetridir (kütleçekimsel olmayan süper simetrik kuramların aksine, örneğin minimal süper simetrik standart model).Süper simetrinin üreteçleri Poincaré grubu ve süper-Poincaré cebiri ile sarılmıştır, süper kütleçekiminin süper simetriyi doğal olarak takip ettiği görülebilir.
Gravitonlar
Kütleçekiminin her kuramı gibi süper kütleçekimi de kuantumu graviton olan dönüş-2 alanını kapsar. Süper simetri süper eşe sahip olabilmek için gravitona ihtiyaç duyar. Bu alanın dönüşü 3/2 ve kuantumu da gravitinodur.Gravitino alanlarının sayısı süper simetrilerin sayısına eşittir.
Tarihi
Ölçüm Süper simetrisi
Süper simetrinin ilk yerel kuramı 1975 yılında Dick Arnowitt ve Pran Nath tarafından ortaya atılmış ve ölçüm süper simetrisi olarak adlandırılmıştır.
SUGRA
SUGRA, ya da süper kütleçekimi, 1976 yılında Dan Freedman, Sergio Ferrara ve Peter Van Nieuwenhuizen tarafından keşfedilmiştir. Ancak, çeşitli boyut sayıları ve ilave (N) süper simetri yükleri ile ilgili kuramlarr tarafından kısa sürede genellenmiştir. N>1 olan Süper kütleçekimi kuramları genellikle büyütülmüş süper kütleçekimi olarak adlandırılır. (SUEGRA). Bazı süper kütleçekimi kuramları daha boutsal düşürme yolu ile yüksek boyut super kütleçekimi kuramlarına eşlik olarak gösterilir (örneğin N=1 11-boyutlu süper kütleçekimi boyutsal olarak düşürülünce N=8, d= 4 SUGRA). Sonuçlanan kuramlarda bazen 1919’da yapılı 5-boyutlu kütleçekimsel kuram olan Kaluza-Klein kuramları kastedilir, çemberde boyutsal olarak düşüş gerçekleştiğinde 4-boyut ağır olmayan modlar elektromanyetizmin kütleçekimi ile birleşmiş hali kastedilir.
mSUGRA
mSUGRA minimal super kütle çekimi anlamına gelir. N=1 süper kütleçekimi taslağı içerisindeki parçacığın gerçekçi yapısının modeli super Higgs mekanizması tarafından yıkımı 1982 yılında Pran Nath, Ali Chamseddine ve Richard Arnowitt tarafından gerçekleştirilmiştir. Büyük Birleştirme Kuramlarınca bu tür modellerin sınıflar minimal super kütleçekimi olarak bilinir, kütleçekimi gizli bir sektörünün varlığının yıkımına SUSY sayesinde vasıta olur. Minimal kütleçekimi, super Higgs etkisinin doğal bir sonucu olarak yumuşak SUSY yıkımı terimlerini meydana getirir. Elektrozayıf simetrinin ışınımsal kırılımlar tekrar normalleştirme grup denklemlerinden dolayı hızlıca gerçekleşen bir sonuçtur.Sadece dört tane değişken gerektiren ve Büyük Birleştirmedeki düşük enerji olaylarını kararlaştırmaya bir işaret olarak göründüğünden minimal super kütleçekimi öngörülen gücünden dolayı parçacık fiziğinde araştırılan en geniş konulardan biridir.
11d: maksimal SUGRA
Süper kütleçekiminlerinden 11-boyutlu kuram,her şeyin kuramının ilk potansiyel adayı olduğundan kayda değer bir heyecana neden olmuştur.Bu heyecan dört yapıtaşı üzerine inşa edilmiştir, ancak ikisi çoktan gözden düşmüştür:
- Wener Nahm tek bir gravitonlu tutarlı en büyük boyut sayısının 11 boyut olduğunu ve iki dönüşlü parçacıkların daha fazla boyutu olabileceğini göstermiştir. Bu problemlerde iki boyutun zaman benzerliğine sahip olduğu Itzhak Bars tarafından vurgulanıp 12 boyuttan kaçınılmaya çalışılmıştır.
- 1981’de, Ed Witten Standart Model’in ölçüm gruplarını kapsayan en küçük ve yeterli boyut sayısının 11 olduğunu ve güçlü etkileşimler için SU(3) ve SU(2) kere U(1)’in de elektrozayıf etkileşimler için olduğunu gösterdi. Bugünlerde, herhangi bir boyut sayısı için süper kütleçekiminde standart model ölçüm grubuna uyarlanabilen birçok teknik mevcuttur. Örneğin, 1980lerin ortalarında ve sonlarında tip 1 ve heterotic sicim kuramları genellikle kullanılmıştır.Tip II Sicim Kuramı’nda kesin Calabi-Yau çeşitliliklerini sıkıştırarak da elde edilebilirler. Bugünlerde, biri D-membran da ölçüm simetirilerini düzenlemede kullanılabilir.
- 1978’de, Eugéne Cremmer, Bernard Julia ve Joel Scherk (CJS) 11-boyutlu süper kütleçekimi kuramı için klasikleşmiş eylemi bulmuşlardır.Bu bulgu, bugüne kadar süper simetrili, 11 boyutlu bir ve ikiden fazla dönüş alanı olmayan kuram olarak gelmiştir. Diğer 11-boyutlu kuramlar, CJS’nin bu kuramına kuantum mekaniksel eşitsiz olarak bilinir, ancak klasik olarak eşitliklidir. Örneğin, 1980’in ortalarında, Bernard de Wit ve Hermann Nicolai D=11 süper SU(8) değişmezlikle kütleçekimi adında alternatif bir kuram bulmuşlardır.Bu kuram, açıkça Lorentz değişmezi değilken, birçok açıdan da CJS kuramından üstündür, örneğin; klasik hareket denklemlerine başvurmadan boyut sayısını 4’e düşürebilmiştir.
- 1980’de, Peter Freund ve M. A. Rubin 11 boyuttan oluşan sıkıştırımı tüm SUSY üreticilerini koruyarak iki şekilde, 4 ya da 7 boyutu iri ölçekli boyutta bırakarak, olabileceğini göstermişlerdir. Maalesef, sıkışmazlık boyutları karşıt de Sitter boşluğuna dönüşmüştür. Bugünlerde, birçok sıkışımın mümkün olabileceği anlaşılmış ancak Freund-Rubin sıkışımı tüm Süper simetri dönüşümleri için değişmezliğini korur.Bu sayede, ilk iki sonuç 11 boyutun da eşsiz şekilde düşünülmesini sağlar, üçüncü sonuç kuramı özelleştirir ve dördüncü sonuç gözlenebilen evrenin neden dört boyutlu olduğunu açıklar.
Kuramın detaylarının çoğu Peter van Nieuwenhuizen, Sergio Ferrara ve Daniel Z. Freedman tarafından ayrıntılarıyla anlatılmıştır.
SUGRA döneminin bitişi
11 boyutlu super kütleçekimi ile ilgili heyecan birçok hatanın ve açığın bulunmasıyla çok çabuk sönmüştür ve bu modeli de başarısızlığa uğratmıştır. Problemler şunlardır:
- Zamanı ve standart modeli kapsayan sıkışmış düzenekler süper simetri ile uyumlu değildi, ve kuark ve leptonları kapsamıyordu. Başka bir öneri de 7-küre ile sıkışmış boyutları grup SO(8) ile değiştirmek ya da basık 7-küre’yi SO(5) kere SU(2) simetri grubuyla değiştirmekti.
- Şu ana kadar, deneylerde gözlemlenen fiziksel nötrinoların Standart Modeldeki kiralite olayına göre kütlesiz olduklarına inanılıyordu ve solak oldukları söyleniyordu, sıkışmadan krital fermiyon üretmek oldukça zordu, ve sıkışmış düzeneğin eşsiz olması gerekiyordu, ancak 1980’lerin sonuna kadar fizikteki eşsizlik anlaşılmaya başlanmamıştı.
- Super kütleçekimi modelleri genel olarak dört boyutta, kaldırılması zor, ince ayar gerektiren ve gerçek olamayacak kadar büyük kozmolojik sabitlere dayanır. Bu hala bir sorundur.
- Kuramın nicelemesi kuantum alan kuramında ölçüm anormalliklerine neden olmaktadır. Aradan geçen yıllarda fizikçiler bu anormalliklerle başa çıkmayı öğrenmişlerdir
Bu zorlukların bazılarından süper sicimleri içeren 10-boyutlu bir kurama geçiş yapılarak kaçınılabilir. Ancak 10 boyutlu bir kurama geçiş yapmak 11-boyutlu kuramın eşsizliğini yitirmesi anlamına gelir. 10-boyut kuramındaki ilk süper sicim devrimi olarak bilinen asıl ilerleme, Michael B. Green, John H. Schwarz ve David Gross tarafından 10 boyutlu super kütleçekimi modellerinde ölçüm simetrilerini ve bu simetrileri yok eden anormallere sahip sadece üç tane super kütleçekimi kuramının bulunmasıdır. Bunlar SO(32) grupları ve iki E8 kopyası olan < math>E_8 \times E_8</math> dolaysız çarpımdır. Bugün, örneğin D-membranlarını 10-boyutlu kurama da uyarlayabileceğimizi biliyoruz.
İkinci Süper sicim Devrimi
10-boyutlu kuramlar ve kuantum tümlemeleri içeren sicim kuramları 1980’lerin sonunda ortadan kalkmıştır. Bu kuramlarda Yau’nun tahmininden çok daha fazla sıkıştırma olduğunu 23. Uluslararası Solvay Fizik Konferansında Calabi-Yaus kabul etmiştir. Hiçbiri standart modeli tam olarak verememiştir and gerekli uğraş verildiğinde farklı yollarla standart modele ulaşılabilir. Ayrıca, kimse düzensizlik kuramındaki düzenin uygulanabilirliğini anlayamamıştır. 1990’ların başında ise nispeten daha durağan bir döneme girilmiştir; ancak bazı önemli araçlar da geliştirilmiştir. Örneğin, çoğu süper sicim kuramlarının sicim ikiliklerine bağlı oldukları açıkça görülmeye başlanmış, bazıları ise zayıf sicim eşleşmesine bağlanmıştır, yani bir modeldeki fizik diğerine göre güçlü sicim eşleşmesidir. Daha sonra hepsi değişip, ikinci süper sicim devrimine dönüşmüştür. Joseph Polchinski, sicim kuramlarındaki altı yıl önce keşfettiği, p-membranlarının daha ipliklisi olan, super kütleçekimi kuramından bilinen D-membran denilen nesnelerin belirsizliğini fark etmiştir, Bu p-membranlarındaki uygulamalar karışık sicim kuramı tarafından sınırlanmamış ve hatta süper simetri sayesinde süper kütleçekimindeki p-membranlar sicim kuramının anladığının da ötesinde anlaşılabilmiştir. Düzensiz olmayan bu yeni araçla donanımlı, Edward Witten ve başka birçok bilim insanı tüm düzensiz sicim kuramlarının tek bir kuramın farklı şekillerde anlatımı ve gösterimi olduğunu söylemiş ve bu tek bir kuramı M-kuramı olarak adlandırmıştır. Dahası, M-kuramının uzun dalga sınırının 11-boyutlu ilk süper sicim devriminin yararına olan 2- ve 5-membramın eşlik ettiği süper kütleçekimine de karşı çıkmıştır. Tarihsel olarak, super kütleçekimi tam daire olmuştur. Bu sicim kuramının özelliklerini anlayabilmek için yaygın olarak kullanılan ve M-kuramı ve M-kuramının sıkışımlarındaki uzay zamanı boyutlarını düşürmek için kullanılan bir taslaktır,
Süper sicimlere ilişkin
Belirli 10-boyutlu super kütleçekimi kuramları 10-boyutlu süper sicim kuramlarının düşü enerji limitleri olarak görülür; yani kütlesiz olarak baş gösterirler. Sicim kuramlarının gerçek etkili alan kuramları nadiren mevcut olurlar. Sicim ikiliklerinden dolayı, tahmin edilen 11-boyutlu M-kuramının 11-boyutlu süper kütleçekimli düşük enerji sınırı olmak zorundadır. Ancak, bu durum sicim kuramı/m-kuramının süper kütleçekiminin tek mümkün UV bitimi olduğu anlamına gelmez.
4D N = 1 SUGRA
SUGRA gerçekliğine geçmeden önce, genel görelilik ile ilgili önemli detayları tekrarlayalım. Üzerinde (3,1)Dönüş demeti olan türevlenebilir 4 boyutlu M dağıtıcımız var. Bu esas demeti Lorentz simetrisine göre şekillenmiştir. Buna ek olarak, dağıtıcımızda dönüşü (3,1)’in altında olan fiber gerçek dört boyutlu T vektör demetimiz var Eğimi TM’den T’ye ters çevrilebilir doğrusal haritamız var. Bu harita dört boyutlu uzay zamanlar haritasıdır.Yerel Lorentz simetrisi bununla ilişkili ölçüm bağlantısına sahiptir ve buna dönüş bağlantısı denir. Aşağıdaki konu süper uzay gösterimi ile ilgili olacak ve bileşen gösterimin karşıtı olarak SUSY’nin altında eşdeğişkeni açıkça gösterilemeyecektir. Süper kütleçekimi’nin aslında birbirine eş olmayan ve burulma açısı tensörünün farklı olmasına neden olan birçok farklı versiyonu vardır, ancak önünde sonunda bir versiyondan diğerine geçerken elde edilen dönüş bağlantısı ve süper dört boyutlu uzay gösteriminin alan tanımlamasını her zaman eşitlik olarak gösterebiliriz.
4D N=1 Süper kütle çekimi’nde 4|4 gerçek türevlenebilir süper dağıtıcı M’de 4 gerçek bozonik boyut ve 4 gerçek fermiyonik boyuta sahibiz. Süper simetrik olmayan durumda olduğu gibi M’de (3,1) dönüşümüz var. M’deki T vektör demetinden ise R4|4 kadar var. Lorentz yerel grubunun altındaki T dönüşümlerinin fiberi şöyledir; dört gerçek bozonik boyut vektöre dönüşür ve dört gerçek fermiyonik boyur Majorana spinoruna dönüşür.Bu Majorana spinorları karmaşık solak Weyl spinoru ve onun sağlak bileşeni Weyl spinoru olarak tekrar ifade edilebilir. (Birbirine bağımlılardır). Bu dönüş bağlantılarına eskisi gibi sahibiz.
Aşağıdaki düzenler; uzaysal (bozonik ve fermiyonik) indeksler M,N,… ile gösterilir. Bozonik uzaysal indeksler μ, ν, ... ile, solak Weyl uzaysal indeksleri α, β, ... ile ve sağlak Weyl uzaysal indeksleri 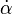 ,
, 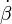 , ... ile gösterilir. T’nin fiberi için olan indeksler de benzer bir gösterime sahiptir, ancak şapkalı olarak gösterilirler;
, ... ile gösterilir. T’nin fiberi için olan indeksler de benzer bir gösterime sahiptir, ancak şapkalı olarak gösterilirler; 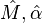 Süper dört boyutlu uzay
Süper dört boyutlu uzay 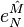 ile gösterilirken, dönüş bağlantısı
ile gösterilirken, dönüş bağlantısı 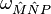 ile gösterilir ve ters süper dört boyutlu uzay ise
ile gösterilir ve ters süper dört boyutlu uzay ise 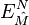 ile gösterilir.
Süper dört boyutlu uzay ve dönüş bağlatısı gerçek durumlarda mantıklı bir şekilde denklemleri sağlar;
< math>e^{\hat{M}}_N (x,\overline{\theta},\theta)^* = e^{\hat{M}^*}_{N^*}(x,\theta,\overline{\theta})</math> ,
ile gösterilir.
Süper dört boyutlu uzay ve dönüş bağlatısı gerçek durumlarda mantıklı bir şekilde denklemleri sağlar;
< math>e^{\hat{M}}_N (x,\overline{\theta},\theta)^* = e^{\hat{M}^*}_{N^*}(x,\theta,\overline{\theta})</math> , 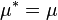 ,
, 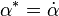 , ve
, ve 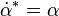 and
and 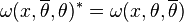 .
Eşdeğişken türevi şöyle tanımlanır;
.
Eşdeğişken türevi şöyle tanımlanır;
![D_\hat{M}f=E^N_{\hat{M}}\left( \partial_N f + \omega_N[f] \right)](../I/m/8f1314c80a90bbed7c8b886249c7eb73.png) .
.
Eşdeğişken dış türevi ise süper dağıtıcıların süper değerlendirilmesi ile tanımlanır. Bu demek olur ki, iki fermiyonik indeksi değiştirdiğimiz her zaman, +1 işaret faktörünü -1 yerine yazarız. R simetrilerinin yokluğu ya da varlığı isteğe bağlıdır, ancak eger R-simetrisi varsa tam süper uzayın bütünleyicisi 0’ın R-yüküne sahip olmak zorundadır ve bütünleyicinin üstü kiral süper uzay ise 2’nin R-yüküne sahip olmak zorundadır.
Kiral süper alan X 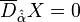 ‘na uyan bir süper alandır. Bu bileşeni kısıtlamak için “c” katsayılarını bütünleyici durumlara ihtiyaç duyarız;
‘na uyan bir süper alandır. Bu bileşeni kısıtlamak için “c” katsayılarını bütünleyici durumlara ihtiyaç duyarız; 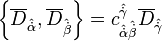 .
SUSY olmayan kütleçekiminin aksine, en azından fermiyonik yönlere göre burulma açısı sıfır olamaz. Zaten, düz bir uzayda bile
.
SUSY olmayan kütleçekiminin aksine, en azından fermiyonik yönlere göre burulma açısı sıfır olamaz. Zaten, düz bir uzayda bile 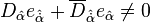 ‘dır. Süper kütleçekiminin bir versiyonun da burulma açısı tensörlerinin üzerindeki kısıtlamalar şöyledir;
‘dır. Süper kütleçekiminin bir versiyonun da burulma açısı tensörlerinin üzerindeki kısıtlamalar şöyledir;
Burada, 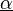 stenografi gösterimi Weyl spinorlarının sola mı sağa mı dizileceğini gösterir. Süper dört boyutlu uzayın,
stenografi gösterimi Weyl spinorlarının sola mı sağa mı dizileceğini gösterir. Süper dört boyutlu uzayın,  , süper belirleyici faktörü bize M’in hacim faktörünü verir. Eşit bir biçimde 4|4 hacmimiz olur ve süper biçimi şöyledir;
, süper belirleyici faktörü bize M’in hacim faktörünü verir. Eşit bir biçimde 4|4 hacmimiz olur ve süper biçimi şöyledir; 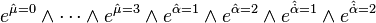 .
Eğer bu süper difeomorfizmleri ölçümü
.
Eğer bu süper difeomorfizmleri ölçümü 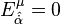 ,
, 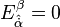 ve
ve 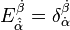 . olacak şekilde daha karmaşık hale getirirsek süper uzay kiralımız x ve Θ koordinatlarına sahip olur.
R süper dört boyutlu uzaydan ve dönüş bağlantısından türevlenebilen yönsüz süper alan kiralidir.
If f is any superfield, is always a chiral superfield.
Eğer f herhangi bir süper alansa,
. olacak şekilde daha karmaşık hale getirirsek süper uzay kiralımız x ve Θ koordinatlarına sahip olur.
R süper dört boyutlu uzaydan ve dönüş bağlantısından türevlenebilen yönsüz süper alan kiralidir.
If f is any superfield, is always a chiral superfield.
Eğer f herhangi bir süper alansa, 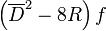 her zaman kiral süper alandır.
Kiral süper alanlı süper kütleçekimi kuramı için “X”;
her zaman kiral süper alandır.
Kiral süper alanlı süper kütleçekimi kuramı için “X”;
K Kahler potansiyeline, W süper potansiyele ve 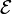 kiral hacim faktörüne eşittir. Düz süper uzaydaki olayın aksine, Kahler ya da süper potansiyel sabitlerini eklemek artık fiziksel bir olaydır. Sabit süper kozmolojik potansiyel değişikliğine kayarken, Kahler potansiyelinin sabit değişimi etkili Planck sabitini değiştirir. Kiral süper alan X’in değeri Planck sabitine bağlıdır, bu yüzden Planck sabitini elde edebilmek için süper dört boyutlu uzayı tekrar ölçeklendirmek gerekir. Buna Einstein çerçevesi denir.
kiral hacim faktörüne eşittir. Düz süper uzaydaki olayın aksine, Kahler ya da süper potansiyel sabitlerini eklemek artık fiziksel bir olaydır. Sabit süper kozmolojik potansiyel değişikliğine kayarken, Kahler potansiyelinin sabit değişimi etkili Planck sabitini değiştirir. Kiral süper alan X’in değeri Planck sabitine bağlıdır, bu yüzden Planck sabitini elde edebilmek için süper dört boyutlu uzayı tekrar ölçeklendirmek gerekir. Buna Einstein çerçevesi denir.
4 boyutta N = 8 Süper Kütleçekimi
N=8 süper kütleçekimi kütleçekimi ve sonlu alan sayısını içeren en simetrik kuantum alan kuramıdır.Sıfıra giden boyutları 11boyutlu süper kütleçekiminden 7’ye düşürerek bu bulunabilir. 8 süper simetri içeren bu kuram dönüş 2 ve dönüş -2 arasında 8 yarım adım olduğundan en kütleçekimsel kuramdır. Bu kuramda 2 dönüşü olan Graviton en yüksek dönüş sayısına sahiptir. Daha fazla süper simetri demek parçacıkların süper eşlerinin dönüşünün 2’den fazla olması demektir. Dönüşü 2’den fazla olan Sicim Kuramı gibi kuramlar sonsuz sayıda parçacık içerir. Stephen Hawking, Zamanın Kısa Özeti kitabında, bunun Her şeyin Kuramı olabileceğinden bahsetmiştir. Ancak ileriki yıllarda Sicim kuramında gözden düşmüştür. 21. yüzyılda da bu kuramın son olacağı ile ilgili düşünceler tekrardan canlanmıştır.
Yüksek Boyutlu SUGRA
Yüksek boyutlu SUGRA genl göreliliğin yüksel boyutlu ve süper simetrik bir genellemesidir. Süper kütleçekimi 11’e kadar her sayı için denklem haline getirilebilir. Yüksel boyutlu SUGRA süper kütleçekiminin dört boyutludan daha büyük olduğuna odaklanmıştır. Spinorlardaki süper yüklerin sayısı uzay zamanındaki boyuta ve işarete bağlıdır. Süper yükler spinorlarda olur. Bu yüzden süper yüklerdeki sınırlar keyfi seçilmiş boyutun uzay zamanında sağlanamaz. Uyumlu bazı kuramsal örnekler: • 12-boyutlu iki zaman kuramı • 11-boyutlu maksimal SUGRA • 10-boyutlu SUGRA kuramları • Tip IIA SUGRA: N = (1, 1) • 11-boyuttan Tip IIA SUGRA • Tip IIB SUGRA: N = (2, 0) • Tip 1 ölçüm SUGRA: N = (1, 0) • 9 boyutlu SUGRA kuramları • 10 boyuttan maksimal 9 boyut SUGRA • T-ikiliği • N = 1 ölçüm SUGRA Dikkat çeken süper kütleçekimi kuramlarının iki daha fazla dönüşü yoktur. Bu demektir ki; aşamalarının simetrik tensörleri hiçbir alanda ikiden fazla Lorentz dönüşümü içermez. Ancak, yüksek dönüş kuramlarındaki etkileşim tutarlılığı oldukça aktif bir alanın ilgisini çeker.
Kaynakça
İngilizce Vikipedi
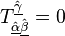
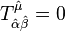
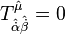
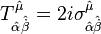
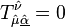
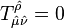
![S = \int d^4x d^2\Theta 2\mathcal{E}\left[ \frac{3}{8} \left( \overline{D}^2 - 8R \right) e^{-K(\overline{X},X)/3} + W(X) \right] + c.c.](../I/m/abff7de71afc73ad7d176fcf5ce0815c.png)