Stern-Gerlach deneyi

Stern-Gerlach deneyi^[1] Alman fizikçi Otto Stern ve Walther Gerlach tarafından isimlendirilen taneciklerin sapmasının kuantum mekaniği alanında önemli bir deneydir. 1922 yılında Otto Stern ve Walther Gerlach tarafından gerçekleştirilen bu deney, genellikle parçaçıkların saçınımını kullanarak kuantum mekaniğinin temel noktalarını açığa çıkarması açısından önemlidir. Bu deney elektronların ve atomların özünde kuantum özelliklerine sahip olduğunu ve ölçülürken kuantum mekaniğinin sistemi nasıl etkilediğini ispat etmek için yapılmaktadır.

Basit Teori ve Tanımlama

Kuantum dönme ve Stern–Gerlach experiment içindeki klasik magnet.

Stern–Gerlach deneyinin temel elementleri.

Stern-Gerlach deneyi homojen olmayan manyetik alana doğru tanecik demetleri göndermeyi ve bu taneciklerin sapmalarını gözlemlemeyi içerir. Sonuçlar taneciklerin özünde klasik olarak dönen objelerin açısal momentumuna yakından benzeyen fakat sadece kesin değerlerle nicelendirilen açısal momentuma sahip olduğunu gösterir. Bir diğer önemli sonuç ise, sadece bir parçacığın dönme bileşeni aynı anda ölçülebilir bunun anlamı z ekseni boyunca dönme ölçümü, x ve y eksenleri boyunca parçacığın dönme bilgilerini yok eder.

Stern-Gerlach deneyi normal olarak elektriksel nötr parçacık ya da atomların iletilmesi için kullanılmaktadır. Bu manyetik alana doğru hareket eden yüklü parçacığın yörüngesi ve dönme-bağımlı etkilere izin vererek hakim olmak için büyük sapmalardan kaçınır. Eğer parçacık klasik olarak dönen dipol olarak davranırsa, manyetik alanın dipolün üzerine uyguladığı dönme momentumu dolayısıyla manyetik alan gibi devinecektir. Parçacık homojen manyetik alana doğru hareket ettiği takdirde, dipolün zıt uçlarındaki birbirlerini nötrleyen yüklere etki eden kuvvet kaybolur ve parçacığın yörüngesi etkisiz hale getirilecektir. Fakat, manyetik alan homojen olmadığı takdirde, dipolün bir ucundaki kuvvet diğer uçtaki kuvvetten parçacığın yörüngesinin yönünü değiştiren net kuvvet olması için ihmal edilecek kadar büyük olacaktır. Eğer parçacık klasik olarak dönebilen objeler olsaydı, açısal momentum vektörlerinin dağılımının belirsiz ve devamlı olması beklenirdi. Her bir parçacık dedektör ekranında bazı yoğunluk dağıtıcı üreten farklı miktar tarafından saptırılır. Bunun karşılığında, Stern-Gerlach düzeneğine giden parçacıkların belirli miktarlar tarafından aşağı ya da yukarı yönü değiştirilir. Bu, kuantumun gözlenebilirliğinin ölçüsüydü. Günümüzde, dönebilen olarak bilinir ve gözlenebilirliğin nokta spektrumu olduğu yerde ölçümün mümkün sonucunun olduğunu kanıtlar. Atomik spektrum gibi aralıklı kuantum olayları olmasına rağmen, Stern-Gerlach deneyi bilim adamlarına süperpose olmuş kuantum durumlarının ölçümlerini yürütmek için bilim tarihinde ilk kez izin vermiştir.

Günümüzde teoriksel olarak kuantum açısal hızına sahip olan herhangi bir tür "belli bir dereceye kadar enerji içermek" olarak da bilinen kesik spektruma sahiptir.

Eğer deney elektron gibi yüklü taneciklerle iletilirse, halkada yönü çevirmeye eğilimli Lorentz kuvveti oluşur. Bu kuvvet yüklü parçacığın yolunu çapraz duruma getirmek için uygun büyüklükteki elektrik alanı tarafından etkisiz hale getirilebilir.

Fermiyonlar için dönme değerleri.

Elektronlar dönen parçacıklardır. (Stern-Gerlach ile serbest elektronların varolamayacağı not edilmelidir.^[2]) Bunlar herhangi bir eksen boyunca ölçülen, tamamen quantum mekaniksel olay olan, ve mümkün olabilen dönme açısal momentum değerleridir. Çünkü bu değerler hep aynıdır, elektronların kesin değerleri olarak görülür ve bazen kesin açısal momentum olarak da bilinir. (Diğer taneciklerin mevcut olmasına bağlı ve çeşitli olabilen orbital açısal momentumdan ayırmak için). Elektronlar için eksenle ölçülen dönme açısal momentum için iki olası değer vardır.  Aynı bilgi üçer kuark içeren nötron ve proton için doğrudur. Fakat, üç kuarklar birbirlerini nötrleyen çiftlere sahip değildir ve karşıt parçacığa net yarım dönme veren üçüncü kuark ‘Proton dönüm noktasından önce inanılan olarak keşfedilmiştir. Çünkü, nükleonların asıl dönmeleri asıldan çok orbitaldir. Diğer parçacıklar mümkün olan farklı dönme değerlerine sahiptir. Delta baryonları, +³⁄₂ parçacıklar ve dört mümkün momentum değeri olarak dönerler. Vektör mezonları, W ve Z bozonları gibi -1 dönme sayısına ve üç mümkün olan dönme açısal momentum değerine sahip olan parçacıklardır.

Matematiksel olarak yarım dönme sayısına sahip parçacıkları tanımlamak için, Dirac’ın bra-ket gösterimini kullanmak en kolayıdır. Parçacıklar Stern-Gerlach düzeneğine doğru giderken, dönmenin aşağı mı yukarı mı olduğunu çözen dedektör tarafından gözlemlenirler. Bunlar izin verilen mümkün değerleri, +ħ/2 ya da −ħ/2, alabilen açısal momentum numarası, j, tarafından tanımlanır. Matematiksel terim olarak:

${\displaystyle |\psi \rangle =c_{1}\left|\psi _{j=+{\frac {\hbar }{2}}}\right\rangle +c_{2}\left|\psi _{j=-{\frac {\hbar }{2}}}\right\rangle }$

C değerleri compleks numaralardır. Mutlak değerlerinin karesi, j'nin iki olası değerlerinin bulunabildiği durumdaki ihtimaline karar verir. Sabitler değerlerin bulunabilmesi için normalleştirilmelidir. Bu nedenle sadece mutlak değerlerde verimli olmaktadır.

Sıralı Deneyler

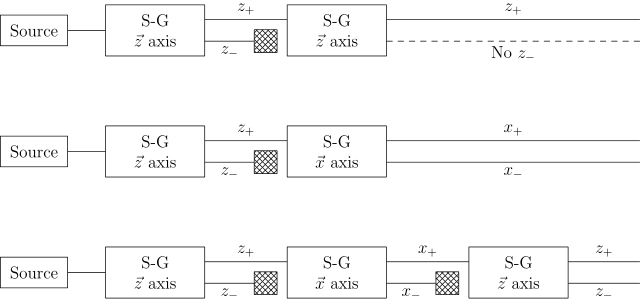
Eğer birçok Stern-Gerlach düzeneklerini birleştirirsek, açıkca görebiliriz ki, düzenekler basit ayırıcılar olarak davranmazlar. Fakat kuantum mekaniği yasalarına göre^[3] değişen durum, ışık kutuplaşması gibi, gözlenir.

Tarihçe

Frankfurt Üniversitesinde deneyi anmak için bulunan plaka.

Stern-Gerlach deneyi 1922 yılında Otto Stern ve Walther Gerlach tarafından Frankfurt, Almanya'da gerçekleştirildi. Bu yıllarda Stern, Frankfurt Üniversitesi Teoretiksel Fizik Enstitüsü'nde Max Born’un asistanıydı. Gerlach is aynı üniversitenin Deneysel Fizik Enstitüsü'nde asıstandı.

Deneyin yapıldığı zamanlarda atomu tanımlayan en öncelikli model, elektronların pozitif yüklü çekirdeklerin etrafında sadece kesin ayrık atomik orbitallerde veya enerji seviyelerinde olduğunu belirten Bohr atom modeliydi. Elektronlar uzayda kesin pozisyonda olmak için belirli dereceye kadar enerji içerdiğinden beri, ayrık orbitlerin içindeki farklılıklar uzay kuvantumlama olarak refere edilir. Stern-Gerlach deneyi gümüş atomunun açısal momentumunun yönünün belirli dereceye kadar enerji içerdiği anlamına gelen Bohr-Sommerfeld hipotezini test etmek için yapılmıştır.^[4]

Deneyin Uhlenbeck ve Goudsmit dönen elektronun varolduğu hipotezini formüle dökmeden yıllar önce yapıldığı not edilmelidir. Stern-Gerlach deneyinin sonuçları daha sonradan quantum mekaniğinin yarım dönebilen parçacık tahminlerine katılır bir hale dönüşse de, deney Bohr-Sommerfeld teorisinin onayı olarak görülmelidir.^[5]

1927 yılında, T.E. Phipps ve J.B. Taylor, gümüş atomunun kullanımının neden olabileceği herhangi bir şüpheyi gümüş atomları^[6] kullanarak eleyerek böylece en alt seviyedeki hidrojen atomlarının kullanım etkilerini yeniden üretmiştir.

Önemi

Modern fizikte, deneyden sonraki gelişmeler Stern-Gerlach deneyinden önemli ölçüde etkilenmiştir.

• Deneyi takip eden on yıl içerisinde, bilim adamları bazı atomların çekirdeğini ayrıca belirli dereceye kadar enerji içeren açısal momentuma sahip olmasına benzer teknikler kullanarak göstermiştir. Bu çekirdek açısal momentum ile spektroskopik çizgideki aşırı ince yapıdan sorumlu elektronların etkileşimidir.
• 1930 yıllarında Stern-Gerlach düzeneklerinin gelişmiş versiyonu kullanılarak, Isidor Rabi ve arkadaşları çeşitli manyetik alanlar kullanarak bir tanesinin bir düzeyden diğerine geçmesi için manyetik momentuma güç uygulayabileceğini göstermiştir. Deney serileri 1937 yılında, Isidor Rabi ve arkadaşları geçişlerin düzeyi çeşitli alanlar ya da RF alanıyla tetiklenebileceğini keşfettiklerinde en son noktaya eriştirilmiştir.
• Norman F. Ramsey, Rabi düzeneğini alan ile birlikte zaman etkileşimini arttırmak için geliştirmiştir. Radyasyon tekrar sıklığından (frekansından) dolayı oluşan uç hassaslık doğru zamanı elde etmek için kullanışlı olmuştur. Günümüzde hala atomik saatlerde kullanılmaktadır.
• 1960 yılından önce, Ramsey ve Daniel Kleppner Stern-Gerlach sistemini günümüzde popüler olan atomik saatlerde de kullanılan hidrojen MASER’in enerji kaynağı olduğundan polarize olmuş hidrojen demeti üretmek için geliştirmiştir.
• Dönme hakkındaki doğrudan gözlem, kuantum mekaniğinde kuvantumlamanın en doğrudan kanıtı olmasıdır. Stern-Gerlach deneyi kuantum ölçüsünün paradigması haline gelmiştir. Özellikle, von Neumann projeksiyonunu sağlamak için varsayılır. Daha ileri sezgilere göre, kuantum mekaniksel homojen olmayan manyetik alan^[7] etkileşiminin tanımına dayanır. Bu sadece kesin algılamada doğru olabilir. Von Neumann projeksiyonu sadece manjetik alan homojen olduğunda kesin olduğunda sağlanır. Çünkü, Von Neumann projeksiyonu düzenli fonksiyonlara sahip Stern-Gerlach düzeneğiyle bile uyumsuzdur.

Kaynaklar

1.  Gerlach, W.; Stern, O. (1922). "Das magnetische Moment des Silberatoms". Zeitschrift für Physik 9: 353–355. Bibcode:1922ZPhy....9..353G. doi:10.1007/BF01326984.
2.  http://journals.aps.org/prl/pdf/10.1103/PhysRevLett.81.4772 - Comment on "Stern-Gerlach Effect for Electron Beams"
3.  Sakurai, J.-J. (1985). Modern quantum mechanics. Addison-Wesley. ISBN 0-201-53929-2.
4.  Stern, O. (1921). "Ein Weg zur experimentellen Pruefung der Richtungsquantelung im Magnetfeld". Zeitschrift für Physik 7: 249–253. Bibcode:1921ZPhy....7..249S. doi:10.1007/BF01332793.
5.  Weinert, F. (1995). "Wrong theory—right experiment: The significance of the Stern–Gerlach experiments". Studies in History and Philosophy of Modern Physics 26B: 75–86. doi:10.1016/1355-2198(95)00002-B.
6.  Phipps, T.E.; Taylor, J.B. (1927). "The Magnetic Moment of the Hydrogen Atom". Physical Review 29 (2): 309–320. Bibcode:1927PhRv...29..309P. doi:10.1103/PhysRev.29.309.
7.  Scully, M.O.; Lamb, W.E.; Barut, A. (1987). "On the theory of the Stern–Gerlach apparatus". Foundations of Physics 17 (6): 575–583. Bibcode:1987FoPh...17..575S. doi:10.1007/BF01882788.

Dış Bağlantılar

• Animasyon, uygulamalar ve dönme ile ilgili araştırma (Paris-Sud Üniversitesi)
• Stern-Gerlach Deneyi Java Uygulaması Animasyonu
• [http://phet.colorado.edu/simulations/sims.php?sim=SternGerlach_Experiment Stern–Gerlach Experiment Flash Model Stern-Gerlach Deneyi Parlama Modeli]
• [http://galileo.phys.virginia.edu/classes/252/Angular_Momentum/Angular_Momentum.html Detailed explanation of the Stern–Gerlach Experiment Stern–Gerlach deneyinin detaylı açıklaması]
• [http://plato.stanford.edu/entries/physics-experiment/figure13.html Image of experiment result Deney sonuçlarının fotoğrafları]
• http://www.kip.uni-heidelberg.de/matterwaveoptics/teaching/archive/ws07-08/SternGerlach.pdf

Notlar

• Bu makale ilgili ingilizce Vikipedi makalesinden çevrilmektedir.

1. Gerlach, W.; Stern, O. (1922). "Das magnetische Moment des Silberatoms". Zeitschrift für Physik 9: 353–355. Bibcode:1922ZPhy....9..353G. doi:10.1007/BF01326984
2. http://journals.aps.org/prl/pdf/10.1103/PhysRevLett.81.4772 - Comment on "Stern-Gerlach Effect for Electron Beams"
3. Sakurai, J.-J. (1985). Modern quantum mechanics. Addison-Wesley. ISBN 0-201-53929-2.
4. Stern, O. (1921). "Ein Weg zur experimentellen Pruefung der Richtungsquantelung im Magnetfeld". Zeitschrift für Physik 7: 249–253. Bibcode:1921ZPhy....7..249S. doi:10.1007/BF01332793.
5. Weinert, F. (1995). "Wrong theory—right experiment: The significance of the Stern–Gerlach experiments". Studies in History and Philosophy of Modern Physics26B: 75–86. doi:10.1016/1355-2198(95)00002-B.
6. Phipps, T.E.; Taylor, J.B. (1927). "The Magnetic Moment of the Hydrogen Atom". Physical Review 29 (2): 309–320. Bibcode:1927PhRv...29..309P. doi:10.1103/PhysRev.29.309.
7. Scully, M.O.; Lamb, W.E.; Barut, A. (1987). "On the theory of the Stern–Gerlach apparatus". Foundations of Physics 17 (6): 575–583. Bibcode:1987FoPh...17..575S. doi:10.1007/BF01882788