Öngörü aralığı

İstatistikte tahmin aralığı, gözlemlenemeyen anakütle parametresinin tahmininde kullanılan güven aralığı yaklaşımından esinlenir.

Örnek

Normal dağılımlı anakütleden bir örnek elde edildiğini varsayalım. Anakütlenin ortalaması ve satandart sapması örnekleme dayalı olarak tahmin edilmediği sürece belirsizdir. Bir sonraki gözlemin tahmin edilmesi arzulanmaktadır. n örneklem boyutu; μ ve σ sırasıyala örneklemin gözlemlenemeyen ortalaması ve standart sapması olsun. X₁, ..., X_n, örneklem; X_n+1 tahmin edilecek ilerki zamandaki gözlem olsun:

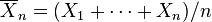
$\overline{X}_n=(X_1+\cdots+X_n)/n$

ve

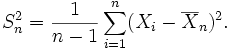$S_n^2={1 \over n-1}\sum_{i=1}^n (X_i-\overline{X}_n)^2.$ olduğu için,

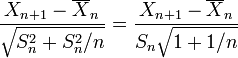${X_{n+1}-\overline{X}_n \over \sqrt{S_n^2+S_n^2/n}} = {X_{n+1}-\overline{X}_n \over S_n\sqrt{1+1/n}}$ gösteriminin n-1 serbestlik derecesinde t dağılımı gösterdiği ortaya konulabilir.

Sonuçta A, 100(1 - (p/2))inci persentili (yüzdeliği) göstermek üzere

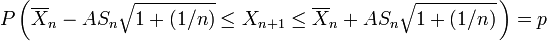$P\left(\overline{X}_n-A S_n\sqrt{1+(1/n)}\leq X_{n+1} \leq\overline{X}_n+A S_n\sqrt{1+(1/n)}\,\right)=p$ elde edilir. Buradan da

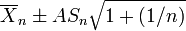$\overline{X}_n\pm A {S}_n\sqrt{1+(1/n)}$ ifadesinin tahmin aralığının uçları olduğu gösterilmektedir.