Aristarkus'dan Büyüklükler ve Uzaklıklar Üzerine

Aristarkus'un MÖ. 3.yy'da yazdığı kitabında Güneş, Yer ve Ay'ın göreli büyüklüklerini gösterdiği şekil, 10.yy'dan kalma bir kopyadan görülmektedir.

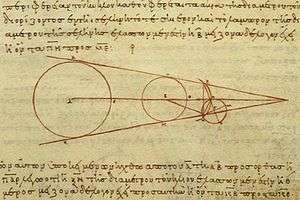
(Güneş ve Ay'ın) Büyüklükleri ve Uzaklıkları Üzerine (Περὶ μεγεθῶν καὶ ἀποστημάτων [ἡλίου καὶ σελήνης], Peri megethon kai apostematon), MÖ. 280-240 yaşamış Sisamlı Aristarkus'ın günümüze kadar ulaşmış kitabıdır. Kitapta Güneş ve Ay'ın büyüklüklerini gösterir çizimler ve hesaplamalar yer alırken, Dünya'nın yarıçapı biriminde uzaklıkları da verilmiştir.

Aristarkus'un bu kitapta bahsettiği açıklama, hesap ve çizimleri kullanarak Yer yarıçapı biriminde çeşitli çıktılara ulaşabiliriz ^[1]. Aşağıda bu hesaplamalar yer almaktadır.

Gösterimler

Çalışmanın yöntemi çeşitli gözlemlere dayanmaktadır:

• Güneşin ve Ayın gökyüzündeki görünür boyutu
• Ay tutulması sırasında Yer'in gölge çapı
• Ayın dördün evresi sırasında Güneş ve Ay arasındaki açı

Ariktarkus'un yöntemini ve çıktılarını hesaplamak için kullanılanacak değişenler:

Sembol	Anlamı
φ	Ay'ın dördün evresi sırasında Ay ve Güneş arasındaki açı (doğrudan ölçülebilir)
L	Ay'a olan uzaklık
S	Güneş'e olan uzaklık
ℓ	Ay'ın yarıçapı
s	Güneş'in yarıçapı
t	Dünya'nın yarıçapı
D	Yerin merkezinden Yerin gölge konisi tepesine olan uzaklık
d	Ayın karşıkonumunda Yerin gölge yarıçapı
n	Oran, d/ℓ (a directly observable quantity during a lunar eclipse)
x	Oran, S/L = s/ℓ (which is calculated from φ)

Ay'ın Dördün Evresi

Aristarkus, Ay'ın dördün evresinde Güneş ve Yer ile birlikte bir dik üçgen oluşturduğu önermesiyle başlamıştı. Ay ile Güneş arasındaki açıyı, φ gözleyerek, Güneş ve Ay'a olan uzaklık oranları trigonometri yardımıyla bulunabilir.

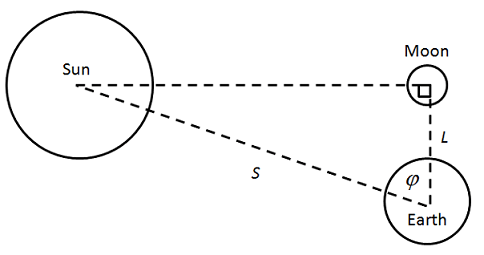
Çizimden ve trigonometriden,

${\displaystyle {\frac {S}{L}}={\frac {1}{\cos \varphi }}=\sec \varphi .}$

yazılabilir. Çizim oldukça abartılmıştır; çünkü gerçekte S = 390 L ve φ 90°'ye çok yakındır. Aristarkus, φ'yı bir dördünün otuzda biri olarak hesapladı (yaklaşık 3°'ye denk gelmektedir). Bu değer gerçek değer olan 87°'den biraz azdır. Trigonometrik fonksiyonlar henüz bulunmamıştı; fakat Aristarkus, Öklid geometrik analizini kullanarak,

${\displaystyle 18<{\frac {S}{L}}<20.}$

olarak buldu. Diğer bir deyişle, Güneş'e olan uzaklık, Ay'a olan uzaklıktan 18 ile 20 kez daha büyüktür ki bu değer, teleskop icat edilip daha hassas ölçümler yapılan kadar, 2000 yıl boyunca astronomlar tarafından kabul edilmiş ve kullanılmıştır.

Aristarkus, ayrıca Güneş ve Ayın açısal büyüklüklerinin aynı olduğunun farkına vardı. Bu sayede Güneş'in Ay'dan 18-20 kez daha büyük olması gerektiği sonucuna ulaştı.

Ay Tutulması

Aristarkus, bir diğer yaklaşımı ay tutulamsı geometrisi üzerine yaptı:

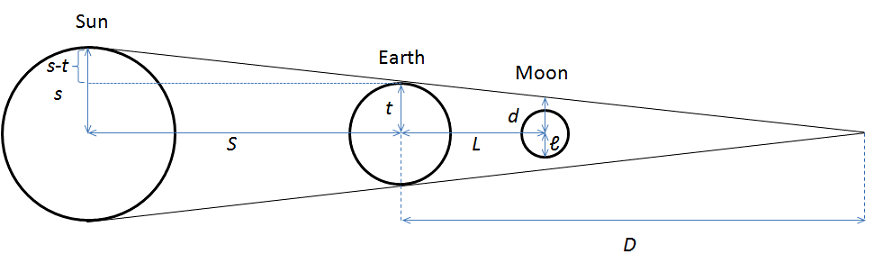
Üçgenlerin benzerliğinden, ${\displaystyle {\frac {D}{L}}={\frac {t}{t-d}}\quad }$ ve ${\displaystyle \quad {\frac {D}{S}}={\frac {t}{s-t}}.}$

Bu iki denklemi bölerek ve Güneş ve Ayın görünür boyutlarını eşit kabul ederek, ${\displaystyle {\frac {L}{S}}={\frac {\ell }{s}}}$, yazılır ve

${\displaystyle {\frac {\ell }{s}}={\frac {t-d}{s-t}}\ \ \Rightarrow \ \ {\frac {s-t}{s}}={\frac {t-d}{\ell }}\ \ \Rightarrow \ \ 1-{\frac {t}{s}}={\frac {t}{\ell }}-{\frac {d}{\ell }}\ \ \Rightarrow \ \ {\frac {t}{\ell }}+{\frac {t}{s}}=1+{\frac {d}{\ell }}.}$

En sağdaki denklemi ayrıca ℓ/t

${\displaystyle {\frac {t}{\ell }}(1+{\frac {\ell }{s}})=1+{\frac {d}{\ell }}\ \ \Rightarrow \ \ {\frac {\ell }{t}}={\frac {1+{\frac {\ell }{s}}}{1+{\frac {d}{\ell }}}}.}$

ya da s/t

${\displaystyle {\frac {t}{s}}(1+{\frac {s}{\ell }})=1+{\frac {d}{\ell }}\ \ \Rightarrow \ \ {\frac {s}{t}}={\frac {1+{\frac {s}{\ell }}}{1+{\frac {d}{\ell }}}}.}$

olarak yazabiliriz. Bağıntıları basitleştirirsek: n = d/ℓ and x = s/ℓ.

${\displaystyle {\frac {\ell }{t}}={\frac {1+x}{x(1+n)}}}$

${\displaystyle {\frac {s}{t}}={\frac {1+x}{1+n}}}$

Yukarıdaki denklemler, gözlenebilir nicelikler üzerinden Güneş ve Ay'ın çaplarını vermektedir.

Sonraki denklemler, Güneş ve Ayın uzaklıklarını Yer ölçülerinde vermektedir:

${\displaystyle {\frac {L}{t}}=\left({\frac {\ell }{t}}\right)\left({\frac {180}{\pi \theta }}\right)}$

${\displaystyle {\frac {S}{t}}=\left({\frac {s}{t}}\right)\left({\frac {180}{\pi \theta }}\right)}$

Burada θ Ay ve Güneş'in derece cinsinden görünür yarıçapıdır.

Çıktılar

Yukarıdaki bağıntılar, Aristarkos'un bulgularını açıklamak için kullanılır. Çizelge bu bulguları göstermektedir. Burada modern bulguların dışında n = 2, x = 19.1 (φ = 87°) ve θ = 1° olarak alınmıştır.

Nicelik	İlişki	Bulgular	Günümüz Değerleri
s/t	Yer yarıçapı biriminde Güneş'in yarıçapı	6.7	109
t/ℓ	Yer yarıçapı biriminde Ay'ın yarıçapı	2.85	3.50
L/t	Yer yarıçapı biriminde Yer-Ay uzaklığı	20	60.32
S/t	Yer yarıçapı biriminde Yer-Güneş uzaklığı	380	23,500

Daha sonraları, Hipparkos, Hipparkos'un Büyüklükler ve Uzaklıklar Üzerine kitabında Ay'a olan ortalama uzaklığı 67 Yer yarıçapı kadar bulmuştu. Batlamyus ise bu değeri 59 Yer yarıçapı olarak kullanmıştı.

Notlar

1. Aristarchus of Samos Yöntemi ile Ay ve Güneş'in Büyüklük ve Uzaklıkları