Asal Zeta Fonksiyonu

Matematik'te, Asal zeta fonksiyonu Riemann zeta fonksiyonu'nun bir analoğudur. sonsuz seriler içinde tanımlanır, yakınsaklık için 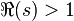$\Re(s) > 1$ olmalıdır:

$P(s)=\sum_{p\,\in\mathrm{\,asal}} \frac{1}{p^s}$.

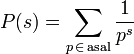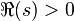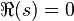Meromorfik devamlılık için$\Re(s) > 0$, ve $\Re(s) = 0$ tabii sınırlardır.

Asal Zeta fonksiyonunun Integrali

$\int\sum_{p\,\in\mathrm{\,asal}}\frac{1}{p^s}\;\mathbf{d}s=-\sum_{p\,\in\mathrm{\,asal}}\frac{1}{p^s\log p}+\mathbf{C}$

$\int_{1}^{\infty}\sum_{p\,\in\mathrm{\,asal}}\frac{1}{p^s}\;\mathbf{d}s=\sum_{p\,\in\mathrm{\,asal}}\frac{1}{p\log p}$

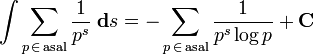
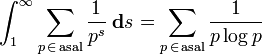
Ayrıca bakınız

• Zeta fonksiyonu

Dış bağlantılar

• Prime Zeta Function, in Wolfram Mathworld