Asal kök

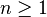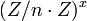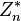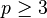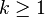Bir asal kök modülü n sayılar teorisindeki modüler aritmetikten bir kavramdır. Eğer $n \ge 1$ olan bir tamsayı ise, n formuna göre aralarında asal sayılar mod n'e göre çarpılarak, bir grup oluşturacak şekilde yapılan işlem,$( Z / n \cdot Z )^x$ veya $Z_n^*$ olarak gösterilir. Bir asal sayı için $p \ge 3$ ve $k \ge 1$ ise, bu grup ancak ve ancak 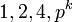$1, 2, 4, p^k \!$, veya 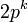$2 p^k\!$ 'ya denktir. Bu döngüsel grubun bir üreteci asal kök modülü n veya 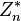$Z_n^*$'in bir asal elemanı'dır şeklinde tanımlanır.

Bir asal kök modülü n, diğer bir değişle, mod n'e göre g gibi öyle bir tamsayıdır ki n'le beraber ortak çarpanı olmayan her tamsayı, g 'nin bir kuvvetine denktir.

Örneğin

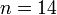$n=14\!$ alalım.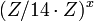$(Z/14 \cdot Z)^x$ 'in elemanları

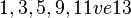$1, 3, 5, 9, 11 ve 13\!$ 'ün denk sınıflarından oluşur.

mod 14'e göre 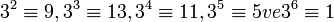$3^2 \equiv 9, 3^3 \equiv 13, 3^4 \equiv 11, 3^5 \equiv 5 ve 3^6 \equiv 1\!$ olduğundan, 3 mod 14'e göre bir asal köktür. Mod 14 için diğer ve tek asal kök ise 5'tir.

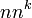$n n^k\!$ (mod 14) - (satırlardaki değerler döngüsel şarta bağlı olarak tekrardan sonra kesilmiştir)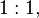

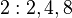
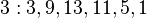
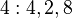
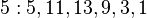
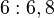
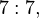
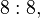
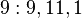
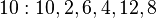
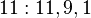
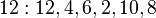
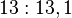
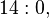
$1 : 1,\!$

$2 : 2, 4, 8\!$

$3 : 3, 9, 13, 11, 5, 1\!$

$4 : 4, 2, 8\!$

$5 : 5, 11, 13, 9, 3, 1\!$

$6 : 6, 8\!$

$7 : 7,\!$

$8 : 8,\!$

$9 : 9, 11, 1\!$

$10 : 10, 2, 6, 4, 12, 8\!$

$11 : 11, 9, 1\!$

$12 : 12, 4, 6, 2, 10, 8\!$

$13 : 13, 1\!$

$14 : 0,\!$

14'le aralarında asal olan sayılar yalnızca kuvvetlerinden biri 1 (mod 14)'e ulaşan sayılardır. Bu sayıların oluşturduğu küme S = (1, 3, 9, 13, 11, 5)'dir.

Problemi f(n, k) = n^k - 1 ≡ 0 (mod 14) gibi ele alırsak, n için tasarlanan köklerin k > 0 olan kuvvetleri için bir polinom sağladığını görürüz. S kümesindeki elemanların tümü, R = {3, 5} kümesindeki sayılardan ve onların kuvvetlerinden elde edilebilir. Ama örneğin 11'den ve onun kuvvetlerinden elde edilemez (mod 14 için). S kümesi tüm kökleri içerir. R kümesi ise asal kökleri içerir. Bunların (mod 14)'e göre tüm kuvvetleri döngüsel olarak tüm kökleri elde eder.