Babenko-Beckner eşitsizliği
Matematik'te, Babenko–Beckner eşitsizliği (K. Ivan Babenko ve William E. Beckner anısına) Fourier dönüşümünün (q, p)-normuna[1] keskin üst sınırları hesaplar. Bu eşitsizlik aynı zamanda Hausdorff–Young eşitsizliğinin keskin formu olarak görülebilir ve entropik belirsizlik prensibinin kanıtında kullanılır. n-boyutlu Fourier dönüşümünün (q, p)-normu şu şekilde tanımlanır
1961'de, Babenko[2] q nun çift tamsayı değerleri için bu normu hesapladı. 1975 yılında Beckner[3], Fourier dönüşümünün özfonksiyonları olan Hermit fonksiyonları'nı kullanarak tüm 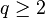 için bu normun değerlerini buldu
için bu normun değerlerini buldu
Başka bir deyişle, Babenko–Beckner eşitsizliği şöyledir
Bu eşitsizliği tek boyutta (yani 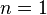 durumunda) açıkça yazarsak
durumunda) açıkça yazarsak
eşitlikleri sağlandığı takdirde,
sağlanır. Başka bir deyişle,
Kanıtın ana fikri
Bu taslak boyunca bir kanıtı,diyelimki
(q için dışında,daha fazla olacak veya Beckner'in gösterimi daha az takip.)
iki-nokta lemması
Diyelimki 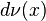 ayrık ölçümü ile
ayrık ölçümü ile 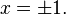 noktasında
noktasında 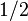 ağırlığı olsun. O zaman işlemci
ağırlığı olsun. O zaman işlemci
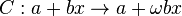
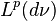 to
to 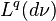 göndermesi norm 1 ile; şudur,
göndermesi norm 1 ile; şudur,![\left[\int|a+\omega bx|^q d\nu(x)\right]^{1/q} \le \left[\int|a+bx|^p d\nu(x)\right]^{1/p},](../I/m/59f21549a0364424388b4802769a019a.png)
veya daha açığı,
a, b herhangi karmaşığı için. ("iki-nokta lemması"nın kanıtı için Beckner'in yazılarına bakınız.)
Bernoulli denemelerinin bir dizisi
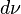 ölçüsü yukarıda tanıtılan aslında bir uygun Bernoulli denemeleri ile ortalama 0 ve değişken 1 dir. n in bir dizisinin toplamı gibi Bernoulli denemeleri dikkate alındığında, bağımsız ve normalize edilmiş böylece standard sapma kalıntısı 1. We obtain the measure
ölçüsü yukarıda tanıtılan aslında bir uygun Bernoulli denemeleri ile ortalama 0 ve değişken 1 dir. n in bir dizisinin toplamı gibi Bernoulli denemeleri dikkate alındığında, bağımsız ve normalize edilmiş böylece standard sapma kalıntısı 1. We obtain the measure 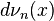 which is the n-fold convolution of
which is the n-fold convolution of 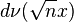 with itself. Son adım temel simetrik polinomlara sırasıyla
with itself. Son adım temel simetrik polinomlara sırasıyla 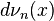 ın (n + 1)-nokta uzayı üzerinde tanımlanan bir operatör yukarda iki-nokta üzerinde tanımlanan C işlemcisine genişletilir.
ın (n + 1)-nokta uzayı üzerinde tanımlanan bir operatör yukarda iki-nokta üzerinde tanımlanan C işlemcisine genişletilir.
Standard normal dağılıma yakınsama
polinomal büyümenin fonksiyonlarına sırasıyla standard normal olasılık dağılımı 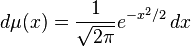 na zayıf yakınsak
na zayıf yakınsak 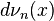 dizisidir.limit içinde,
dizisidir.limit içinde, 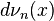 ölçümü sırasıyla temel simetrik polinomların terimleri içinde yukarda C işlemcisinin açılımı standard normal dağılıma sırasıyla Hermite polinomlarının terimleri içinde bir T işlemcisi olarak ifade edilebilir.
Bu Hermite fonksiyonları Fourier dönüşümünün öz fonksiyonlarıdır, ve Fourier dönüşümünün (q, p)-normu bazı renormalizasyon sonrası bir sonuç olarak elde edilir
ölçümü sırasıyla temel simetrik polinomların terimleri içinde yukarda C işlemcisinin açılımı standard normal dağılıma sırasıyla Hermite polinomlarının terimleri içinde bir T işlemcisi olarak ifade edilebilir.
Bu Hermite fonksiyonları Fourier dönüşümünün öz fonksiyonlarıdır, ve Fourier dönüşümünün (q, p)-normu bazı renormalizasyon sonrası bir sonuç olarak elde edilir
Ayrıca bakınız
- Hirschman belirsizliği
Kaynakça
- ↑ Iwo Bialynicki-Birula. Formulation of the uncertainty relations in terms of the Renyi entropies. arXiv:quant-ph/0608116v2
- ↑ K.I. Babenko. An ineqality in the theory of Fourier analysis. Izv. Akad. Nauk SSSR, Ser. Mat. 25 (1961) pp. 531–542 English transl., Amer. Math. Soc. Transl. (2) 44, pp. 115–128
- ↑ W. Beckner, Inequalities in Fourier analysis. Annals of Mathematics, Vol. 102, No. 6 (1975) pp. 159–182.
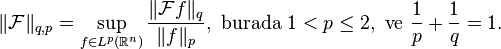
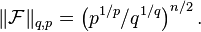
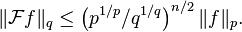
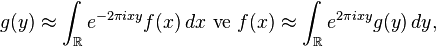
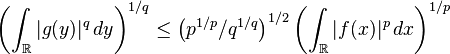
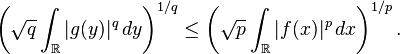
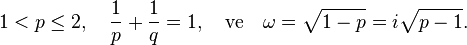
![\left[\frac {|a+\omega b|^q + |a-\omega b|^q} 2 \right]^{1/q}
\le \left[\frac {|a+b|^p + |a-b|^p} 2 \right]^{1/p}](../I/m/476b514cc4336161fccc5da99a6806c0.png)