Bethe formülü

Bethe formülü hızlı yüklü parçacıkların (protonlar, alfa parçacıkları, atomik iyonlar ama elektronlar değil ^{[Dipnot 1]}) malzeme (ya da durdurma gücü malzemesi) ile enerji kaybını açıklar. Yüksek hızlı yüklü parçacıklar maddenin içinde hareket ederken, malzemenin atomlarındaki elektronlarla etkileşirler, bu etkileşme atomu uyarır ya da iyonlaştırır. Bu durum hareket eden parçacığın enerji kaybetmesine yol açar.

Klasik olan, göreli olmayan ilk biçimi 1913 yılında Niels Bohr tarafından^[1]; kuantum mekaniksel olan, göreli olmayan ilk biçimi 1930 yılında Hans Bethe tarafından^[2] ortaya atıldı; 1932 yılında göreli etkileri temel alan deneysel verilerle tutarlı biçime sokuldu^[3]. En olası enerji kaybı, ortalama enerji kaybından farklıdır ve bu Landau-Vavilov dağılımı ile tanımlanır.^[4]

Formül

Formülün göreli biçimi:

   

${\displaystyle -\left\langle {\frac {dE}{dx}}\right\rangle ={\frac {4\pi }{m_{e}c^{2}}}\cdot {\frac {nz^{2}}{\beta ^{2}}}\cdot \left({\frac {e^{2}}{4\pi \varepsilon _{0}}}\right)^{2}\cdot \left[\ln \left({\frac {2m_{e}c^{2}\beta ^{2}}{I\cdot (1-\beta ^{2})}}\right)-\beta ^{2}\right]}$

(1)

   

Burada;

${\displaystyle \beta }$	${\displaystyle =v/c}$
${\displaystyle v}$	parçacığın hızı
${\displaystyle E}$	parçacığın enerjisi
${\displaystyle x}$	yol mesafesi
${\displaystyle c}$	ışık hızı
${\displaystyle z\,e}$	parçacığın yükü
${\displaystyle e}$	temel yük
${\displaystyle m_{e}}$	elektronun durgun kütlesi
${\displaystyle n}$	malzemedeki elektronların sayı yoğunluğu
${\displaystyle I}$	malzemenin ortalama uyarılma potansiyeli

Burada, malzemenin elektron sayı yoğunluğu ${\displaystyle n={\frac {N_{A}\cdot Z\cdot \rho }{A\cdot M_{u}}}}$ ile hesaplanabilir, burada ${\displaystyle \rho }$ malzemenin yoğunluğu, Z ve A sırasıyla atom numarası ve kütle numarası,  ${\displaystyle M_{u}}$ = 1 g/mol molar kütle sabiti ve ${\displaystyle N_{A}}$ Avagadro sayısıdır.

Protonun enerji fonksiyonu olarak protonlar için alüminyumunun durdurma enerjisi, ve Bethe formülü (kırmızı) ve düzeltmeleri (mavi).

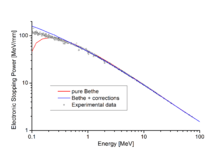
Yandaki resimde, küçük daireler çeşitli yazarlardan elde edilen deneysel veriler (http://www.exphys.jku.at/Stopping/ adresinden alındı); eğri ise Bethe formülünü göstermektedir. Bethe formülünün yüksek enerjilerdeki deneyler ile uyum içinde olduğu açıktır, özellikle düzeltmeler ilave edildiğinde.

Formül sıklıkla, Bloch yaklaşımını içermediği durumlarda bile ${\displaystyle (I=(10ev)\times Z)}$ Bethe-Bloch formülü olarak adlandırılır.

Küçük enerjiler için Bethe formülü şu şekilde basitleştirilebilir ${\displaystyle (\beta \ll 1)}$;

   

${\displaystyle -{\frac {dE}{dx}}={\frac {4\pi nz^{2}}{m_{e}v^{2}}}\cdot \left({\frac {e^{2}}{4\pi \varepsilon _{0}}}\right)^{2}\cdot \left[\ln \left({\frac {2m_{e}v^{2}}{I}}\right)\right]}$

(2)

   .

Bu nedenle, Bethe formülüne göre, enerji artarken durdurma gücü kabaca ${\displaystyle 1/v^{2}}$ ile azalır. Yaklaşık ${\displaystyle E=3Mc^{2}}$'de minimuma ulaşır, burada${\displaystyle M}$ parçacığın kütlesidir (protonlar için 3000 MeV olabilir). Çok göreli enerjiler için, ${\displaystyle (\beta \approx 1)}$, enerji kaybı yine göreli bir şekilde artar.

Bethe formülü yalnızca yüklü parçacığa (iyon) atomik elektronlarla taşınmayan yeterince büyük enerjiler için geçerlidir. Daha küçük enerjilerde, elektron iyon kapısı durumundayken yük etkin bir şekilde azalır ve böylece durdurma gücü de azalır. Ancak parçacık tamamen iyonize olsa bile düzeltmeler gereklidir.

Ortalama uyarılma potansiyeli

eV bölü Z cinsinden atomların ortalama uyarılma potansiyeline I karşı atom numarası Z.

Bethe kuramında malzeme tek bir değer, ortalama uyarılma potansiyeli I ile ifade edilir. 1933 yılında Felix Bloch atomların ortalama iyonizasyon potansiyelinin yaklaşık şöyle olduğunu gösterdi;

   

${\displaystyle I=(10eV)\cdot Z}$

(3)

   

Burada Z malzeme atomlarının atom numarasıdır. Eğer bu yaklaşıklık yukarıdaki formüle (1) yerleştirilirse, Bethe-Bloch formülü olarak adlandırılan ifade elde edilir. Ama Z 'nin bir fonksiyonu olarak I tablolarımız tam olarak elimizde olduğundan (aşağıya bakınız) böyle bir tablonun kullanılması formülün (3) kullanımından daha iyi sonuçlar verecektir.

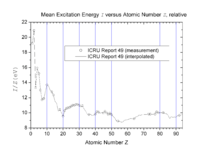
Şekil tablodan alınan normalize I değerlerini gösterir.^[5] Bu şekildeki tepe ve çukurlar durdurma gücünde tepe ve çukurlara karşılık gelen bir yol açar. Bunlar "Z₂ titreşimleri" veya "Z₂ yapısı" (Burada Z₂ = Z olup hedefin atom numarası anlamına gelir) olarak adlandırılır.

Bethe formülündeki düzeltmeler

Bethe kuantum mekaniğinde bir pertürbatif genişleme kullanarak bir formül buldu. Dolayısıyla sonuç ${\displaystyle z}$ kare parçacığın yükü ile orantılıdır. Formül ${\displaystyle z}$'nin yüksek mertebelerine karşılık gelen düzeltmeleri göz önüne alarak zenginleştirilebilir. Bunlar: Barkas-Andersen etkisi (${\displaystyle z^{3}}$ ile orantılı, Walter H. Barkas ve Hans Henrik Andersen), Bloch düzeltmesi (${\displaystyle z^{4}}$ ile orantılı). Ek olarak, malzemenin atomik elektronlarının sabit olmadığını göz önünde tutmak gereklidir ("kabuk düzeltme").

Örneğin, tanıtılan bu düzeltmeleri PSTAR ve ASTAR programları proton ve alfa parçacıklarının durdurma gücünü hesaplamak için kullanır. (www.physics.nist.gov/PhysRefData/Star/Text/programs.html). Düzeltmeler düşük enerjilerde geniştir ve enerji arttıkça daha düşük hâle gelmektedir.

Çok yüksek enerjilerde Fermi yoğunluk düzeltmelerinin eklenmesi gereklidir.^[5]

Literatür

• P. Sigmund: Particle Penetration and Radiation Effects, General Aspects and Stopping of Swift Point Charges (= Springer Series in Solid State Sciences. Vol. 151). Springer, Berlin/Heidelberg 2006, ISBN 978-3-540-72622-7.
• Hans Bethe, Zur Theorie des Durchgangs schneller Korpuskularstrahlen durch Materie, "Annalen der Physik", 397 (1930) 325 - 400

Ayrıca bakınız

• Durdurma gücü
• Landau dağılımı
• Hans Bethe

Dipnotlar

1. Küçük kütleleri, ayırtedilemezlikleri ve Bremsstrahlung (frenleme) ile çok büyük kayıplara uğradıklarından dolayı elektronlar için biraz farklıdır.

Referanslar

1. N. Bohr: II. On the theory of the decrease of velocity of moving electrified particles on passing through matter, The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1913, 25. Jg., Nr. 145, S. 10-31.
2. Özgün makale: Hans Bethe, Zur Theorie des Durchgangs schneller Korpuskularstrahlen durch Materie, "Annalen der Physik", 397 (1930) 325 - 400
3. Sigmund, Peter Particle Penetration and Radiation Effects. Springer Series in Solid State Sciences, 151. Berlin Heidelberg: Springer-Verlag. ISBN 3-540-31713-9 (2006)
4. H. Bichsel, Rev. Mod. Phys. 60, 663 (1988)
5. Report 49 of the International Commission on Radiation Units and Measurements, "Stopping Powers and Ranges for Protons and Alpha Particles", Bethesda, MD, USA (1993)

Dış bağlantılar

• Madde içinde yüklü parçacıkların geçişi (İngilizce)
• Protonlar ve alfa parçacıkları için durdurma gücü (İngilizce)
• Durdurma gücü verileri ve grafikleri (İngilizce)
• Denisov, S. P., "Yüklü parçacıkların iyonizasyon enerjisi kaybı" (Rusça)
• Elektronların madde ile etkileşimi (Rusça)
• Malzeme ile parçacıkların etkileşimi − enerji kaybı (Rusça)
• Özcan, V. E. Parçacıkların maddeyle etkileşimi (Türkçe)
• Radyasyonun madde ile etkileşmesi (İstanbul Üniversitesi Çekirdek Fiziği II) (Türkçe)
• Ocak, S.B. Radyasyon madde etkileşmesi (yüklü parçacıklar). Türk Fizik Derneği VIII. Uluslararası Katılımlı Parçacık Hızlandırıcıları ve Detektörleri Yaz Okulu (Türkçe)
• Gürbüz, S. Algıç Fiziği 2. CERN Türk Öğretmen Çalıştayı 4. (Türkçe)