Chirplet dönüşümü

dalga, dalgacık, cıvıltı, ve cik kıyaslaması

işaret işlemede, chirplet dönüşümü ilkel analizin bir ailesi ile bir giriş sinyalinin bir iç çarpımı cıvıltıcık olarak adlandırılır. ^[1][2]

Diğer dönüşümlere benzerlik

Chirpletler genellikle daha çok dalgacık dönüşümü içinde,(veya ondan olarak ifade edilebildiğinden ) bir tek ana chirpletten (dalgacık teorisinin ana dalgacık olarak adlandırmaya analogudur) üretilir.

Chirplet ve chirplet dönüşümü nedir?

Chirplet dönüşümü terimi Steve Mann tarafından icat edilmişti,chirpletler üzerine ilk basılan yazıların başlığı idi.Chirplet teriminin kendisi (chirplet dönüşümünden ayrı) bir cıvıltı fonksiyonunun bir pencereli kısmın tanıtımı Steve Mann, Domingo Mihovilovic, ve Ronald Bracewell tarafından ayrıca kullanılmış idi . Bu adamların sözleriyle:

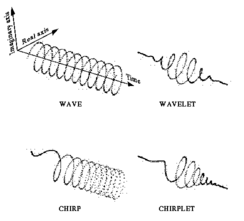
Bir dalganın bir parçası dalgacık, ve bir cik(cıvıltıcık), benzer şekilde, bir cıvıltının bir parçasıdır. Daha doğrusu, bir cıvıltıcık cıvıltı fonsiyonunun bir pencere kısmıdır, burada pencere bazı zaman yerleşim özelliklerini sağlar. zaman–frekans uzayı terimleri içerisinde, cıvıltıcıklar dönme olarak var, kesme, veya geleneksel paralellik ile zaman ve frekans ekseninden taşınan diğer yapılar bu dalga için tipiktir(Fourier ve kısa-süreli Fourier dönüşümleri) veya dalgacıklar.

cıvıltıcık dönüşümü böylece bir dönme, kesme, veya bunun dısında ki dönüşüm gösterimleri zaman– frekans düzleminin döşemesidir. cıvıltı radar işareti içinde birçok yıllar var olduğu bilinmesine rağmen, darbe baskılaması, ve benzerleri, cıvıltıcık dönüşümüne ilk kaynak yayın zaman–frekansı değiştirme modulasyonu veya frekansı değiştirilerek zaman modulasyonu,zaman ve frekans kaymasına ekleme içinde, ve skala değişiklikleri ile bir diğerine ilişkili fonksiyonların ailesi üzerinden temel alan özel işaret gösterimlerini tanımlar. Bu yazıda, Gaussian chirplet dönüşümü böyle bir örnek olarak radar içinde buz parçası saptama için başarılı bir uygulama ile birlikte sunuldu (önceki yaklaşımlar üzerinde hedef saptama sonuçlarını geliştirmek).Chirplet terimi (ama terim chirplet dönüşümü değildir),Mihovilovic ve Bracewell tarafından aynı yıl sonunda görünüşte bağımsız bir benzer dönüşüm içinde önerilmişti.^[2]

Uygulamalar

(a) görüntü işleme olarak, periyodisite genellikle doğrusal ölçeklemeye tabidir. (b) chirp sağa doğru, (sıklığında artış) Bu görüntüdeki, pencere içindeki koyu dalgalı uzay gibi yinelenen yapılar ve beyaz varlığın ışık uzayı. (c) chirplet dönüşümü kompakt modüle varyasyonu temsil edebilmektedir..

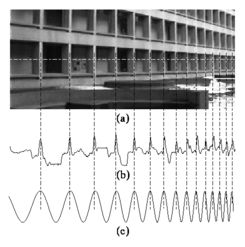
chirplet dönüşümü bir yararlı sinyal analizi ve çerçeve gösterimi şu yaygın spektrumlu iletişim içinde chirp-gibi girişim(desenleri) tüketimi için kullanılmıştır,^[3] EEG süreci içinde,^[4] ve Chirplet Zaman Domenli yansıtımölçer.^[5]

Ayrıca bakınız

• Zaman-frekans gösterimi

Diğer zaman-frekans dönüşümleri:

• Kısa süreli Fourier dönüşümü
• Dalgacık dönüşümleri
• Fraksiyonel fourier dönüşümü

Kaynakça

1. S. Mann and S. Haykin, "The Chirplet transform: A generalization of Gabor's logon transform", Proc. Vision Interface 1991, 205–212 (3–7 June 1991).
2. D. Mihovilovic and R. N. Bracewell, "Adaptive chirplet representation of signals in the time–frequency plane," Electronics Letters 27 (13), 1159–1161 (20 June 1991).
3. Akansu, A. (May 1998), "A novel time-frequency exciser in spread spectrum communications for chirp-like interference", Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) 6 (4): 3265–3268, DOI:10.1109/ICASSP.1998.679561, http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=679561&url=http%3A%2F%2Fieeexplore.ieee.org%2Fxpls%2Fabs_all.jsp%3Farnumber%3D679561 
4. Cui, J. (17 February 2005), "Time–frequency analysis of visual evoked potentials using chirplet transform", Electronics Letters 41 (4): 217–218, DOI:10.1049/el:20056712, http://www.eyetap.org/papers/docs/CuiTime_frequency_chirplet_vep.pdf, erişim tarihi: 2010-07-29 
5. http://zone.ni.com/devzone/cda/epd/p/id/5684

• Mann, S.; Haykin, S. (21–26 July 1991), The adaptive chirplet: An adaptive wavelet like transform, "36th Intl. Symp. Optical and Optoelectronic Appl. Sci. Eng.", Proc. SPIE 1565, DOI:10.1117/12.49794, http://wearcam.org/chirplet/adaptive_chirplet1991/  LEM, Logon Expectation Maximization
• Mann, S.; Haykin, S. (1992). "Adaptive chirplet transform". Optical Engineering 31 (6): 1243–1256. Bibcode 1992OptEn..31.1243M. DOI:10.1117/12.57676. http://wearcam.org/chirplet/adaptive_chirplet1992/.  introduces Logon Expectation Maximization (LEM) and Radial Basis Functions (RBF) in Time–Frequency space.
• Osaka Kyoiku, Gabor, wavelet and chirplet transforms...(PDF)
• J. "Richard" Cui, etal, Time–frequency analysis of visual evoked potentials using chirplet transform, IEE Electronics Letters, vol. 41, no. 4, pp. 217–218, 2005.

Dış bağlantılar

• DiscreteTFDs - software for computing chirplet decompositions and time–frequency distributions
• The Chirplet Transform (web tutorial and info).