De Moivre formülü
Matematikte de Moivre formülü, 18. yüzyıl Fransız matematikçisi Abraham de Moivre anısına isimlendirilmiş ve herhangi bir karmaşık sayı (özellikle herhangi bir gerçel sayı x ve herhangi bir tamsayı n) için şu ifadenin geçerli olduğunu önerir:
Bu formülün önemi (burada önünde i sanal birim ifade ile verilmiş olan) karmaşık sayılar ile trigonometri arasındaki bağlantıyı açıklamasındadır.
Bu formülde "cos x + i sin x" bazen "cis x" olarak kısaltılabilir.
Formülün sol tarafi binom teoremi kullanarak açılıp gerçel kısmına ve sanal kısmına yeni şekil verilirse, cos(nx) ve sin(nx) için yalnızca sin(x) ve cos(x) kullanan uygulamalı matematikde çok önemli ifadeler elde edilir.
Bu formülün diğer bir uygulaması ise De Moivre sayısı adı verilen birimin köklerini (yani 1in köklerini) karmaşık sayılar (yani zn = 1 ise zkarmaşık sayıları) ile ifade edilmesini sağlamasıdır
Tarihi olarak başka şekilde isbat edilmekle beraber, de Moivre'in formülü Euler'in formülünü kullanarak hemen şöyle isbat edilebilir:
ve üstel yasaya göre
O halde Euler'in formülü ile,
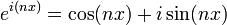 . olur.
. olur.
İndüksiyon ile ispat
Üç değişik hal ele alınabilir:
Eğer n > 0 ise, matematiksel endüksiyon ile şöyle ilerliyebiliriz.
Eğer n = 1 ise, sonuç açıkca geçerlidir. Hipotezimiz icin, sonucun bir tamsayı olan k için geçerli olduğunu varsayalım. Yani varsayımız şu olsun:
Şimdi n = k + 1 halini ele alalim:
![\begin{alignat}{2}
\left(\cos x+i\sin x\right)^{k+1} & = \left(\cos x+i\sin x\right)^{k} \left(\cos x+i\sin x\right)\\
& = \left[\cos\left(kx\right) + i\sin\left(kx\right)\right] \left(\cos x+i\sin x\right) &&\qquad \mbox{enduksiyon hipotezine gore}\\
& = \cos \left(kx\right) \cos x - \sin \left(kx\right) \sin x + i \left[\cos \left(kx\right) \sin x + \sin \left(kx\right) \cos x\right]\\
& = \cos \left[ \left(k+1\right) x \right] + i\sin \left[ \left(k+1\right) x \right] &&\qquad \mbox{ trigonometrik ozdesliklere gore}
\end{alignat}](../I/m/c6a8219a21171669fc80ac9aff31efd3.png)
Bundan, eğer sonucun, n = k için geçerli olması halinde, n = k + 1 için de geçerli olduğu anlamına varılır. Öyle ise, matematik endüksiyon prensipine göre, tüm pozitif tamsayılar için (yani n≥1 için) bu sonuç geçerli olur.
Eğer n = 0 ise, 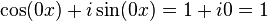 olduğu için ve konvansiyonel olarak
olduğu için ve konvansiyonel olarak 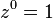 olarak verildiği için, bu formül geçerlidir.
olarak verildiği için, bu formül geçerlidir.
Eğer n < 0 ise, n = -m olduğu zaman bir pozitif tamsayı m ele alsın. O halde
Böylelikle, teorem nin tüm tamsayı değerleri için geçerlidir.
Kosinus ve sinus için tek tek formüller
Karmaşık sayıların eşitliğini gösterdiği için bu denklemin hem gerçel kısımları hem de sanal kısımları ayrı ayrı birbirine eşit olmalıdır. Eğer x (ve bundan dolayı 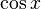 ve
ve 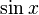 ) gerçel sayılar ise, o zaman bu kısımların özdeşlikleri (taraf değiştirilerek) şöyle yazılabilir:
) gerçel sayılar ise, o zaman bu kısımların özdeşlikleri (taraf değiştirilerek) şöyle yazılabilir:
Bu denklemler xin karmaşık değerleri için geçerlidir. Buna neden, her iki tarafın da x in holomorf fonksiyonları olması ve gerçel eksende birbiriyle çakışan bu şekildeki iki fonksiyonun karmaşık düzeyde de mutlaka birbiriyle çakışması gereğidir.
Bu denklemlerin örnek ifadeleri olarak 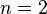 ve
ve 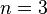 için şu sonuçlar çıkarılır:
için şu sonuçlar çıkarılır:
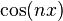 için formülün sağ tarafı gerçekte
için formülün sağ tarafı gerçekte 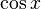 değerli Çebişev polinomu olan
değerli Çebişev polinomu olan 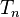 ifadesinin n(cosx) değeridir.
ifadesinin n(cosx) değeridir.
Genelleştirme
Bu formül yukarıda verilen hallerden daha geniş hallerde de geçerlidir. Eğer z ve w karmaşık sayılarsa, o halde
bir çokludeğerli fonksiyon olur ve
ise bir çokludeğerli fonksiyon olmaz. Böylece
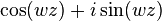 ifadesi sunun bir parcasidir
ifadesi sunun bir parcasidir 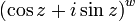 .
.
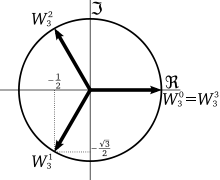
Uygulamalar
Bu formül bir karmaşık sayı için ninci kökleri bulmak için kullanılabilir. Eğer
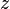 bir karmaşık sayı ise bu polar koordinatlı olarak şu şekilde yazılabilir:
bir karmaşık sayı ise bu polar koordinatlı olarak şu şekilde yazılabilir:
O halde
olur. Burada 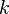 tamsayıdır.
tamsayıdır. 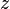 için
için 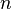 tane değişik kök bulmak için
tane değişik kök bulmak için 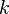 nin
nin 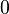 den
den 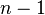 e aralığını incelemek gerekir.
e aralığını incelemek gerekir.
Ayrıca bakınız
- Euler formülü
- Birimin kökü
- Abraham de Moivre
Dış bağlantılar
- Abramowitzm,M. ve Stegun,I.A. (1964) Handbook of Mathematical Functions, New York, Dover Publications, say. 74 (ISBN 0-486-61272-4) İngilizce.
- De Moivre's Theorem for Trig Identities haz.: Michael Croucher, Wolfram Gösterim Projesi İngilizce.
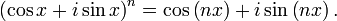
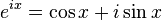
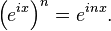
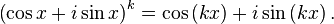
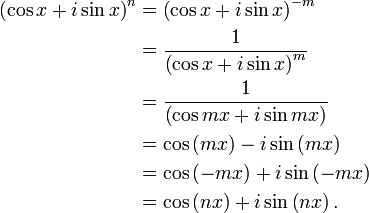
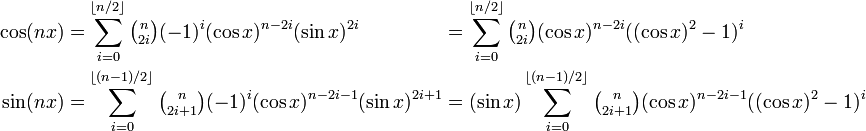
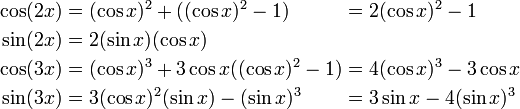
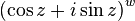
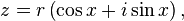
![z^{{}^{\frac{1}{n}}}= \left[ r\left( \cos x+i\sin x \right) \right]^ {{}^{\frac{1}{n}}}= r^{{}^{\frac{1}{n}}} \left[ \cos \left( \frac{x+2k\pi}{n} \right) + i\sin \left( \frac{x+2k\pi}{n} \right) \right]](../I/m/9f3fc2d5894ed834582447eaa1734d8c.png)