Gauss yüzeyi

silindirik bir Gauss yüzeyi genellikle sonsuz bir uzunluktaki, düzlükteki, ideal teldeki elektrik yükünü hesaplamak için kullanılır.

Gauss yüzeyi, üç boyutlu uzayda içinden bir vektör alanın akısı geçen kapalı bir yüzeydir; genellikle elektrik alanı, yerçekim alanı ve manyetik alanı bulmak için kullanılır.^[1] rastgele seçilmiş bu kapalı yüzey S = ∂V ( üç boyutta sınırlandırılan V alanı) Gauss yasasıyla ilişkili alan (Gauss yasası, magnetizma için Gauss yasası, ya da yerçekimi için Gauss yasası) için conjuction olarak bir yüzey integrali sergilenerek kullanılır. Elektrostatik alanın kaynağı olarak elektrik yükünün miktarı ya da yerçekimi alanını kaynağı olarak yerçekimi ağırlığını kapalı alanda hesaplamak için kullanılır. Maddesel olması için, elektrik alan bu metinde, alanın en sık bilinen yüzey şekli olarak tanımlandırıldı. Gauss yüzeyleri genellikle, yüzey integralinin simetrisini basitçe hesaplayabilmek için dikkatle seçildi. Bir Gauss yüzeyi, yüzey üzerindeki her noktanın elektrik alan bileşenleri için,sabit bir normal vektörüne doğru seçilmiş ise, hesaplama zor bir integral gerektirmeyecektir.

Genel Gauss Yüzeyleri

Ayrıca bakınız: yük yoğunluğu

geçerli (solda) ve geçersiz(sağda) Gauss yüzeyleri. Sol: bu geçerli Gauss yüzeyleri, küre yüzeyi, torus yüzeyi ve küp yüzeyleridir ayrıca 3D bir hacmin etrafını tamamıyla kuşatırlar . Sağ: Bu yüzeyler Gauss yüzeyi olarak kullanılamazlar, örneğin disk yüzeyi, kare yüzeyi ve yarımküre yüzeyi ,ayrıca 3D bir hacmin etrafını tamamıyla kuşatamazlar (kırmızı) çizgiyle sınırlandırılmışlardır.

Gauss yüzeyinin kullanıldığı birçok hesaplama Gauss yasası kullanılarak başlar (elektrik için):^[2]

${\displaystyle \Phi _{E}=\,\!}$

${\displaystyle \mathbf {E} \;\cdot \mathrm {d} \mathbf {A} ={\frac {Q(V)}{\varepsilon _{0}}}.\,\!}$

Q(V) içinde bulunan elektrik yükü , V kapalı yüzeydir.

Bu ıraksaklık teoremi ve Coulomb yasasının birleşimi olan Gauss yasası’dır.

Küresel Yüzey

Küresel bir Gauss yüzeyi elektrik alanı ve aşağıdakilerden herhangi biri ile üretilen akıyı bulmak için kullanılır :^[3]

• noktasal bir yük
• küresel kabuğa düzgün yayılmış bir yük
• başka bir yük dağılımı küresel simetri

Küresel Gauss yüzeyi ortak merkezli yük dağılımı için seçilmiştir.

Örnek olarak, kalınlığı ihmal edilen eşit dağılımlı yükü Q ve yarıçapı R olan yüklü küresel bir kabuk S düşünelim. Yüklü kürenin merkezinden r kadar uzaklıkta a noktasında meydana gelen elektrik alanı E bulmak için Gauss yasasını kullanabiliriz. Yarıçapı r < R olan küresel Gauss yüzeyi için etrafı çevrili yük sıfırdır. Bu nedenle net akı sıfırdır ve ayrıca Gauss yüzeyi üzerindeki elektrik alanın büyüklüğü de sıfırdır.(Gauss yasasında Q_A = 0 olarak yazılır. Q_A Gauss yüzeyi tarafından kuşatılan yüktür.)

Aynı örnekle ,daha büyük bir Gauss yüzeyi kullanılarak kabuğun dışında yarıçapı r > R,Gauss yasası sıfıra eşit olmayan bir elektrik alan ortaya koyacaktır. Bu aşağıdakilerle tanımlanır;

S küresel yüzeyinin dışındaki akı

${\displaystyle \Phi _{E}=\,\!}$

${\displaystyle \mathbf {E} \cdot d\mathbf {A} =\int \!\!\!\!\int _{c}EdA\cos 0^{\circ }=E\int \!\!\!\!\int _{S}dA\,\!}$

Yarıçapı r olan kürenin yüzey alanı

${\displaystyle \int \!\!\!\!\int _{S}dA=4\pi r^{2}}$

tanımlar

${\displaystyle \Phi _{E}=E4\pi r^{2}}$

Gauss yasası kullanarak akı

${\displaystyle \Phi _{E}={\frac {Q_{A}}{\varepsilon _{0}}}}$

Son olarak, Φ_E r konumundaki elektrik alanın E büyüklüğünü verir;

${\displaystyle E4\pi r^{2}={\frac {Q_{A}}{\varepsilon _{0}}}\quad \Rightarrow \quad E={\frac {Q_{A}}{4\pi \varepsilon _{0}r^{2}}}.}$

Bu önemsiz olmayan sonuç herhangi bir küresel yük dağılımının noktasal yük olarak rol oynadığını gösterir. Bu aslında Coulomb yasasının bir tanımıdır.

Silindirik Yüzey

Silindirik yüzey, aşağıdakilerden herhangi biri tarafından üretilen akıyı ve elektrik alanı bulabilmek için kullanılan bir Gauss yüzeyidir:^[3]

• aynı yükteki sonsuz bir uzunluğun
• aynı yükteki sonsuz bir yüzeyin
• aynı yükte sonsuz uzunluktaki bir silindirin

Örnek olarak, sonsuz çizgi yüküne yakın olan alan aşağıda verilmiştir. P noktası üzerinde yük yoğunluğuna (yük bölü birim uzunluk) λ sahip sonsuz çizgisinden r kadar uzaklıkta bir yük düşünelim. Silindir formunda kapalı bir yüzey hayal ettiğimizde, yüzeyin dönme ekseni yük hattıdır. Silindirin boyu h ise, silindiri kuşatan yük :

${\displaystyle q=\lambda h}$,

Burada q Gauss yüzeyini kuşatan yüktür. Şekilde a, b and c olarak gösterilen üç yüzey bulunmaktadır. diferansiyel vektör alanı dA, her bir yüzey üzerinde a, b and c.

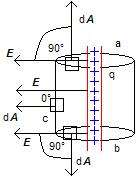
Bu üç parçanın birleşiminden geçen akı

${\displaystyle \Phi _{E}=\,\!}$

${\displaystyle \mathbf {E} \cdot d\mathbf {A} =\int \!\!\!\!\int _{a}\mathbf {E} \cdot d\mathbf {A} +\int \!\!\!\!\int _{b}\mathbf {E} \cdot d\mathbf {A} +\int \!\!\!\!\int _{c}\mathbf {E} \cdot d\mathbf {A} }$

a ve b yüzeyleri için, E ve dA dik olacaktır. c yüzeyi için, E ve dA paralel olacaktır, şekilde gösterildiği gibi.

${\displaystyle {\begin{aligned}\Phi _{E}&=\int \!\!\!\!\int _{a}EdA\cos 90^{\circ }+\int \!\!\!\!\int _{b}EdA\cos 90^{\circ }+\int \!\!\!\!\int _{c}EdA\cos 0^{\circ }\\&=E\int \!\!\!\!\int _{c}dA\\\end{aligned}}}$

Silindirin yüzey alanı

${\displaystyle \int \!\!\!\!\int _{c}dA=2\pi rh}$

Bunu tanımlar

${\displaystyle \Phi _{E}=E2\pi rh}$

Gauss yasasına göre

${\displaystyle \Phi _{E}={\frac {q}{\varepsilon _{0}}}}$

Φ_E için eşitlik sağlanır

${\displaystyle E2\pi rh={\frac {\lambda h}{\varepsilon _{0}}}\quad \Rightarrow \quad E={\frac {\lambda }{2\pi \varepsilon _{0}r}}}$

Gauss kutusu

Aynı yük yoğunluğuyla sonsuz bir yük katmanından oluşan ya da sonlu kalınlıktaki yük levhasından oluşan elektrik alana karar vermek için çoğunlukla bu yüzey kullanılır. Bu kutu silindirik bir şekle sahiptir, üç bileşene sahipmiş gibi de düşünülebilir. Silindirin bir sonundaki diskin alanı πR²,diğer bir sonundaki diskin alanı da bu alana eşittir. Gauss yasası’na göre; yüzeyin bütün bileşenlerine doğru olan elektriksel akı kutuyu kuşatan yükle orantılıdır. Çünkü katmana yakın olan alan neredeyse sabittir.

Ayrıca bakınız

• Area
• Surface area
• Vector calculus
• Integration
• Divergence theorem
• Faraday cage
• Field theory
• Field line

Referanslar

1. Essential Principles of Physics, P.M. Whelan, M.J. Hodgeson, 2nd Edition, 1978, John Murray, ISBN 0-7195-3382-1
2. Introduction to electrodynamics By: Griffiths D.J
3. Physics for Scientists and Engineers - with Modern Physics (6th Edition), P. A. Tipler, G. Mosca, Freeman, 2008, ISBN 0-7167-8964-7

• Purcell, Edward M. (1985). Electricity and Magnetism. McGraw-Hill. ISBN 0-07-004908-4. 
• Jackson, John D. (1998). Classical Electrodynamics (3rd ed.). Wiley. ISBN 0-471-30932-X. 

Ek okuma

• Electromagnetism (2nd Edition), I.S. Grant, W.R. Phillips, Manchester Physics, John Wiley & Sons, 2008, ISBN 978-0-471-92712-9

Dış bağlantılar

• Fields - a chapter from an online textbook