Histogram
Histogram, sayısal verilerin dağılımının grafiksel bir sunumudur. İlk olarak Karl Pearson [1] tarafından tanımlanan histogram, sürekli değişkenin (niceliksel değişken) olasılık dağılımının bir tahminidir. Bir histogram oluşturmak için, ilk adım, değer aralığını belirlemek (tüm değer aralığını bir dizi aralığa bölmek) ve daha sonra, her aralığa kaç değer düştüğünü saymaktır. Kutular genellikle değişkenlerin ardışık, birbiriyle örtüşmeyen aralıkları olarak belirlenir. Depolar (aralıklar) bitişik olmalı ve sıklıkla (eşit olması gerekmez) eşit büyüklükte olmalıdır. [2]
Depolar eşit boyutta ise, dolabın üzerine, frekansla orantılı olarak bir dikdörtgen (-her kutudaki vaka sayısını belirtir) dikilir. Bir histogram’da "göreceli" frekansları görüntülemek için normalleştirilebilir. Ardından, yüksekliklerinin toplamı 1'e eşit olarak, çeşitli kategorilerin her birine düşen vakaların oranını gösterir.
Bununla birlikte kutuların eşit genişlikte olması gerekmez, bu durumda dikilmiş dikdörtgen alanı, alanın kutudaki kutup sayısı ile orantılı olarak tanımlanır [3] Dikey eksen frekansı değil frekans yoğunluğunu belirtir, yatay eksende değişkenin birim başına vaka sayısıdır. Değişken depo genişliği örnekleri aşağıda Sayım Bürosu verilerinde gösterilmektedir.
Bitişik kutular boşluk bırakmadığından, histogramın dikdörtgenleri, orijinal değişkenin sürekli olduğunu belirtmek için birbirine dokunur.[1]
Histogramlar, verilerin altında yatan dağılımın yoğunluğu ve çoğunlukla yoğunluk tahmini için kaba bir anlam taşır: Altta yatan değişkenin olasılık yoğunluk fonksiyonunu tahmin etme. Olasılık yoğunluğu için kullanılan bir histogramın toplam alanı daima 1'e normalleştirilir. X ekseni üzerindeki aralıkların uzunluğu 1 ise, histogram, göreceli frekans arsasıyla aynıdır.
Bir histogram, kutular üzerindeki frekansları yumuşatmak için bir çekirdek kullanan basit bir çekirdek yoğunluk tahmini olarak düşünülebilir. Bu genel olarak daha altta yatan değişken dağılımını yansıtacak daha yumuşak bir olasılık yoğunluk fonksiyonu üretir. Yoğunluk tahmini, histograma bir alternatif olarak çizilebilir ve genellikle bir kutu kümesi yerine bir eğri olarak çizilir.
Bir diğer alternatif olan ortalama kaymış histogram ise, çekirdeği kullanmadan yoğunluğun yumuşak bir eğri tahminini verir.
Histogram, kalite kontrolünün yedi temel aracından biridir.
Histogramlar bazen çubuk grafiklerle karıştırılır. Bir çubuk grafikte kategorik değişkenlerin bir arsa olduğu kabul edilirken, histogram'da sürekli veriler için kutular veri aralıklarını temsil eder. Bazı yazarlar, çubuk grafiklerinde, ayırımı netleştirmek için dikdörtgenler arasında boşluklar bulunmasını önermektedir.
Kökeni
Histogram kelimesinin kökeni belirsizdir. Bazen Antik Yunan’da ἱστός (histos) (bir şeyin dikilmesi-bir geminin direkleri, bir tezgâhın çubuğu veya bir histogramın dikey çubukları) veya γράμμα (gramma)(Çizim, kaydetme, yazma) kelimesinden türetildiği söylenir. 1891'de terimi tanıtan Karl PEARSON'un histogramı tarihsel diyagram’dan türettiği de söylenmektedir.[2]
Örnekler
Bu oyuncak bir örnektir:
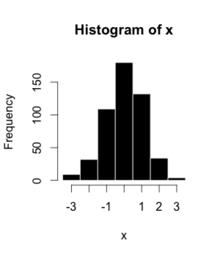
| Kutu | Sayısı |
|---|---|
| -3.5 | 23 |
| -2,5 | 32 |
| -1,5 | 109 |
| 0,5 | 180 |
| 0.5 | 132 |
| 1.5 | 34 |
| 2.5 | 4 |
| 3.5 | 90 |
Histogramlar, desenlerini tanımlamak için kullanılan kelimelerle sınıflandırılır. Çeşitleri şunlardır: "simetrik", "sola eğik" veya "sağa", "tek yönlü", "çift yönlü" ya da "çok yönlü".
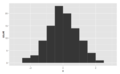 Simetrik, unimodal
Simetrik, unimodal Çarpık değil
Çarpık değil Çarpık sol
Çarpık sol Çift yönlü
Çift yönlü Taşıyıcı
Taşıyıcı Simetrik
Simetrik
Bu konuda daha fazla bilgi edinmek için birkaç farklı kutu genişlikleri kullanarak verileri çizmek için iyi bir fikirdir. Verilen ipuçlarına bir örnek bir restoran.
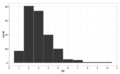 1 $bin genişliğini kullanarak ipuçları doğru çarpık, unimodal
1 $bin genişliğini kullanarak ipuçları doğru çarpık, unimodal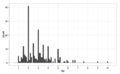 10 bin genişliğini kullanarak, ipuçları hala 50c $ ve miktarda modu ile değil de, herhangi bir çarpık, yuvarlama gösterir, ayrıca biraz aykırı
10 bin genişliğini kullanarak, ipuçları hala 50c $ ve miktarda modu ile değil de, herhangi bir çarpık, yuvarlama gösterir, ayrıca biraz aykırı
İşte birkaç tane daha örnek:
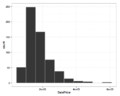 Ames 2009 sergiler satılan evlerin fiyatlarının doğru eğ
Ames 2009 sergiler satılan evlerin fiyatlarının doğru eğ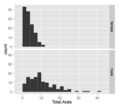 Grand slam tenis turnuvasında oyuncular tarafından aslar, cinsiyete göre küt. Orada daha fazla ACE erkekler oyun.
Grand slam tenis turnuvasında oyuncular tarafından aslar, cinsiyete göre küt. Orada daha fazla ACE erkekler oyun.
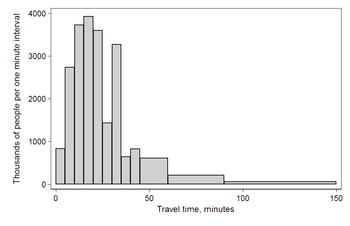
ABD Sayım Bürosu, evlerinin dışında çalışan 124 milyon insanın bulunduğunu tespit etti.[3] Aşağıdaki tabloda, yolculukların işe koyduğu zamana ilişkin verileri kullanıldığında, seyahat süresi "en az 30 fakat 35 dakikadan az" ile yanıt verenlerin mutlak sayıları yukarıdaki ve aşağıdaki kategorilerin sayısından daha yüksektir. Bunun nedeni büyük olasılıkla bildirilen yolculuk süresini yuvarlayan kişilerdir. Değerlerin keyfi olarak yuvarlak rakamlarla bildirilmesi sorunu, insanlardan veri toplarken sık görülen bir durumdur.
-
Mutlak sayılara göre veri Aralık Genişlik Miktar Miktar/genişlik 0 5 4180 836 5 5 13687 2737 10 5 18618 3723 15 5 19634 3926 20 5 17981 3596 25 5 7190 1438 30 5 16369 3273 35 5 3212 642 40 5 4122 824 45 15 9200 613 60 30 6461 215 90 60 3435 57
Bu histogram, her bir bloğun alanı, anketteki kategorisine giren ankette bulunan kişiye eşit olacak şekilde, birim aralık başına vaka sayısını her bir bloğun yüksekliği olarak gösterir. Eğri altındaki alan toplam vakaların sayısını (124 milyon) temsil etmektedir. Bu tür histogram mutlak sayıları gösterir; Q, binlercesindedir.
-
Orana göre veriler Aralık Genişlik Miktar (Q) Q/toplam/genişlik 0 5 4180 0.0067 5 5 13687 0.0221 10 5 18618 0.0300 15 5 19634 0.0316 20 5 17981 0.0290 25 5 7190 0.0116 30 5 16369 0.0264 35 5 3212 0.0052 40 5 4122 0.0066 45 15 9200 0.0049 60 30 6461 0.0017 90 60 3435 0.0005
Bu histogram yalnızca dikey ölçekte birinciden farklıdır. Her bloğun alanı, her kategorinin temsil ettiği toplamın fraksiyonudur ve tüm çubukların toplam alanı 1'e eşittir ("all" anlamına gelen kesir). Gösterilen eğri basit bir yoğunluk tahmini. Bu sürüm orantıları gösterir ve birim alan histogramı olarak da bilinir.
Diğer bir deyişle, bir histogram, genişlikleri sınıf aralıklarını temsil eden ve alanları ilgili frekanslarla orantılı olan dikdörtgenler vasıtasıyla bir frekans dağılımını temsil eder: her birinin yüksekliği, aralık için ortalama frekans yoğunluğudur. Aralıklar, histogram tarafından temsil edilen verilerin, özel iken, aynı zamanda bitişik olduğunu göstermek için bir araya getirilir. (Örneğin, bir histogramda 10.5-20.5 ve 20.5-33.5 arası iki bağlantı aralığına sahip olmak mümkündür ancak 10.5-20.5 ve 22.5-32.5 arası iki bağlantı aralığında bulunmak mümkün değildir Boş aralıklar boş olarak gösterilir ve atlanmazlar.)[4]
Matematiksel tanım
Daha genel matematiksel bir anlamda, bir histogram, ayrık kategorilerin her birine (kutular olarak bilinir) düşen gözlem sayısını sayan bir işlev "mi" olurken, bir histogramın grafiği, bir histogramı temsil etmek için sadece bir yoldur. Böylece, toplam gözlem sayısı ve "k" nin toplam kutu sayısı olmasına izin verilirse, histogram "mi" aşağıdaki koşulları karşılar:
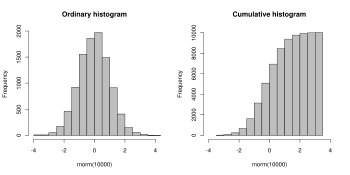
Birikmiş histogram
Birikimli histogram, belirtilen kutuya kadar tüm kutulardaki gözlem sayısını sayan bir haritalandırmadır. Yani, bir histogramın mj kümülatif histogramı Mi şu şekilde tanımlanır:
Depo sayısı ve genişliği
"En iyi" sayıda kutu yoktur ve farklı kutular boyutu verilerin farklı özelliklerini ortaya çıkarabilir. Veri gruplama en azından 17. yüzyılda Graunt'un çalışmaları kadar eskidir ancak[5] Sturges'in 1926'da çalışmasına kadar hiçbir sistematik yönerge verilmemiştir.[6]
Yoğunluğun düşük olduğu kutuları daha geniş kullanırsanız, örnekleme rasgeleliği nedeniyle gürültüyü azaltır; Yoğunluğun yüksek olduğu (dolayısıyla sinyal gürültüyü bastıran) daha dar bölmeleri kullanarak yoğunluk tahmini için daha fazla hassasiyet sağlanır. Dolayısıyla, bir histogram içindeki bölme genişliğini değiştirmek yararlı olabilir. Bununla birlikte, eşit genişlikteki kutular yaygın olarak kullanılmaktadır.
Bazı teorisyenler, en uygun kutu sayısını belirlemeye çalıştı ancak bu yöntemler genelde dağılım şekli hakkında güçlü varsayımlar yapıyor. Gerçek veri dağıtımına ve analizin hedeflerine bağlı olarak, farklı bidon genişlikleri uygun olabilir, bu nedenle uygun bir genişliği belirlemek için deney yapılmalıdır. Bununla birlikte, çeşitli faydalı yönerge ve başparmak kuralları vardır.[7]
Depo sayısı k doğrudan atanabilir veya önerilen kutu genişliği h olarak hesaplanabilir:
Ayraçlar, tavan fonksiyonunu belirtir.
- Kare-Kök seçimi
(Excel histogramları ve diğerleri tarafından kullanılan) örneklemdeki veri noktalarının sayısının karekökünü alır.[8]
- Sturges formülü
Sturges formülü[6] binom dağılımından türemiştir ve örtük olarak yaklaşık normal bir dağılım var sayar.
Depo boyutlarını veri aralığında örtülü olarak temel alır ve n <30 olduğunda, depoların sayısı -yedi'den küçük olacak- ve verilerin iyi eğilimler gösterme ihtimali düşüktür. Veriler normal olarak dağıtılmadığında kötü performans gösterebilir.
- Pirinç Kuralı
Pirinç Kuralı[9], Sturges'in kuralına basit bir alternatif olarak sunulmaktadır.
- Doane formülü
Doane formülü[10] normal olmayan verilerle performansını arttırmaya çalışan Sturges formülünün bir modifikasyonudur.
Burada g_ {1} dağılımın tahmini 3.-moment-çarpıklığıdır ve
- Scott'ın normal referans kuralı
Burada örneklem standart sapmasıdır. Scott'ın normal referans kuralı,[11] normal dağılımlı verilerin rasgele örneklerinde, yoğunluk tahmininin karmaşık karesini en aza indirgediği için en uygun çözümdür.[5]
Bütünleştirilmiş ortalama karesel hatayı asgariye indirmenin bu yaklaşımı Normal dağılımların ötesinde genelleştirilebilir:[12]
Burada, depodaki veri noktalarının sayısıdır ve J'nin en küçük olduğu h değerinin seçilmesi, toplam karesel ortalama karesini en aza indirir.
- Freedman–Diaconis seçimi
Freedman-Diaconis kuralı şöyledir:[13]
Bu da IQR ile ifade edilen çeyrekler arası aralığa dayanmaktadır. Scott'ın kuralının 3.5σ'ının, verilerdeki belirsizlikler için standart sapmadan daha az hassas olan 2 IQR ile değiştirilir.
- Tahmini L2[14] risk fonksiyonunun küçültülmesine dayalı bir seçim
Burada ve bir histogramın ortalama ve ön yargılı varyansı, kutu genişliği ve .
- Açıklama
Kutuların sayısının ile ters orantılı olması için iyi bir neden şudur: verilerin pürüzsüz yoğunluklu sınırlanmış bir olasılık dağılımının bağımsız gerçeklemeleri olarak elde edildiğini varsayalım. Sonrasında sonsuzluk eğilimi gösterdiği için histogram eşit derecede "engebeli" kalır. Eğer dağılımın "genişliği" ise (örneğin, standart sapma veya dörtlüler arası aralık), bir bölmedeki birim sayısı (frekans) olarak ve bağıl standart hata düzeni . Bir sonraki kutuya kıyasla, yoğunluğun türevinin sıfır olmaması koşuluyla frekansın göreli değişimi düzeyindedir. böylece .
Bu basit kübik kök seçeneği, sabit genişlikte olmayan kutulara da uygulanabilir.
Başvurular
- ↑ Charles Stangor (2011) "Research Methods For The Behavioral Sciences".
- ↑ M. Eileen Magnello (December 2006). "Karl Pearson and the Origins of Modern Statistics: An Elastician becomes a Statistician". The New Zealand Journal for the History and Philosophy of Science and Technology 1 volume. OCLC 682200824. http://www.rutherfordjournal.org/article010107.html.
- ↑ US 2000 census.
- ↑ Dean, S., & Illowsky, B. (2009, February 19).
- 1 2 Scott, David W. (1992). Multivariate Density Estimation: Theory, Practice, and Visualization. New York: John Wiley.
- 1 2 Sturges, H. A. (1926). "The choice of a class interval". Journal of the American Statistical Association: 65–66. DOI:10.1080/01621459.1926.10502161. JSTOR 2965501.
- ↑ e.g. § 5.6 "Density Estimation", W. N. Venables and B. D. Ripley, Modern Applied Statistics with S (2002), Springer, 4th edition.
- ↑ EXCEL 2007: Histogram
- ↑ Online Statistics Education: A Multimedia Course of Study (http://onlinestatbook.com/).
- ↑ Doane DP (1976) Aesthetic frequency classification.
- ↑ Scott, David W. (1979). "On optimal and data-based histograms". Biometrika 66 (3): 605–610. DOI:10.1093/biomet/66.3.605.
- ↑ https://maikolsolis.wordpress.com/2014/04/26/optimizing-histogram-cross-validation/
- ↑ Freedman, David; Diaconis, P. (1981). "On the histogram as a density estimator: L2 theory". Zeitschrift für Wahrscheinlichkeitstheorie und verwandte Gebiete 57 (4): 453–476. DOI:10.1007/BF01025868.
- ↑ Shimazaki, H.; Shinomoto, S. (2007). "A method for selecting the bin size of a time histogram". Neural Computation 19 (6): 1503–1527. DOI:10.1162/neco.2007.19.6.1503. PMID 17444758. http://www.mitpressjournals.org/doi/abs/10.1162/neco.2007.19.6.1503.
Daha fazla okuma
- Lancaster, H. O. Giriş için Sağlık İstatistikleri. John Wiley ve Oğulları. 1974. ISBN 0-471-51250-8