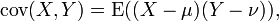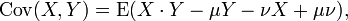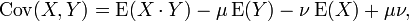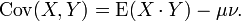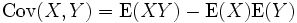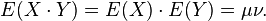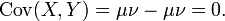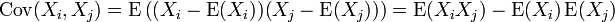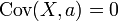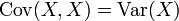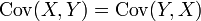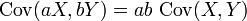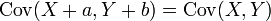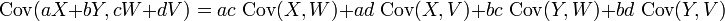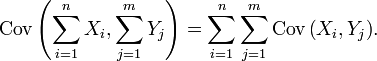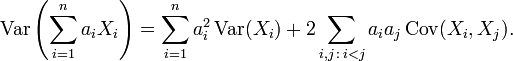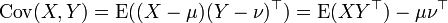Kovaryans

Olasılık teorisi ve istatistikte, kovaryans iki değişkenin birlikte ne kadar değiştiklerinin ölçüsüdür. Kovaryans, iki rastgele değişkenin beraber değişimlerini inceleyen bir istatistiktir. (Özel bir hal olarak iki değişken birbirine özdeşlerse kovaryans o tek özdeş değişkenin varyansı olur.)

Tanımlama

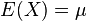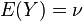Kovaryans, beklenen değerleri $E(X)=\mu$ ve $E(Y)=\nu$ olan X ve Y olarak tanımlanmış iki gerçel değerli rassal değişken arasındaki ilişki tanımlanır:

$\operatorname{cov}(X, Y) = \operatorname{E}((X - \mu) (Y - \nu)), \,$

Burada E, beklenen değeri temsil etmektedir. Bu tanınım alternatif olarak şöyle de yazılabilir:

$\operatorname{Cov}(X, Y) = \operatorname{E}(X \cdot Y - \mu Y - \nu X + \mu \nu), \,$

$\operatorname{Cov}(X, Y) = \operatorname{E}(X \cdot Y) - \mu \operatorname{E}(Y) - \nu \operatorname{E}(X) + \mu \nu, \,$

$\operatorname{Cov}(X, Y) = \operatorname{E}(X \cdot Y) - \mu \nu. \,$

$\operatorname{Cov}(X, Y) = \operatorname{E}(XY) - \operatorname{E}(X) \operatorname{E}(Y) \,$

Kovaryansı sıfır olan iki rassal değişkene korelasyonsuz değişkenler adı verilir.

Eger X ve Y bağımsızlarsa o zaman kovaryansları sıfır olur. Bu bağımsızlık halinde şu tanımsal ifadenin geçerli olmasından elde edilir:

$E(X \cdot Y)=E(X) \cdot E(Y)=\mu\nu. \,$

Kovaryans tanımı için verilen son ifade göz önüne getirilerek ve bunu uygun yere koyarak şu netice elde edilir:

$\operatorname{Cov}(X, Y) = \mu \nu - \mu \nu = 0. \,$

Fakat bunun aksi doğru değildir. Bazı değişkenler için kovaryans sıfır olmakla beraber, bunlar bağımsız değildirler. Ancak kovaryansın sıfır olması yanında bazı diğer özel koşulların da konulması ile (örneğin çokdeğişirli normal dağılımları göstermeleri koşulu) sıfır değerde kovaryans bağımsızlık ifade eder.

Kovaryans Cov(X, Y) ölçümünün birimi X çarpı Y sonucunun ölçüm birimidir. Buna karşılık, kovaryans kavramından ortaya çıkarılan, doğrusal bağımlılık ölçüsü olan korelasyon'un ölçü birimi boyutsuzdur.

Kovaryansın hesaplanması küçük parçalar haline hesaba konulan değerlerle yapılabilir ve bu süreç şu formüle göre yapılabilir:

$\operatorname{Cov}(X_i, X_j) = \operatorname{E}\left((X_i-\operatorname{E}(X_i))(X_j-\operatorname{E}(X_j))\right) = \operatorname{E}(X_iX_j) -\operatorname{E}(X_i)\operatorname{E}(X_j)$

Bu formül kovaryans hesaplama formülü olarak da anılır.

Özellikler

Eğer X, Y, W ve V gerçel değerli rassal değişkenlerse ve a, b, c ve d sabit iseler (bu halde sabit kavramı rastsal olmama anlamındadır) aşağıdaki ifadeler, kovaryansın tanımından elde edilebilir:

$\operatorname{Cov}(X, a) = 0 \,$

$\operatorname{Cov}(X, X) = \operatorname{Var}(X)\,$

$\operatorname{Cov}(X, Y) = \operatorname{Cov}(Y, X)\,$

$\operatorname{Cov}(aX, bY) = ab\, \operatorname{Cov}(X, Y)\,$

$\operatorname{Cov}(X+a, Y+b) = \operatorname{Cov}(X, Y)\,$

$\operatorname{Cov}(aX+bY, cW+dV) = ac\,\operatorname{Cov}(X,W)+ad\,\operatorname{Cov}(X,V)+bc\,\operatorname{Cov}(Y,W)+bd\,\operatorname{Cov}(Y,V)\,$

Bir seri değişkenler X₁, ..., X_n ve Y₁, ..., Y_m rastsal değişkenler ise şu ifade ortaya çıkartılabilir:

$\operatorname{Cov}\left(\sum_{i=1}^n {X_i}, \sum_{j=1}^m{Y_j}\right) = \sum_{i=1}^n{\sum_{j=1}^m{\operatorname{Cov}\left(X_i, Y_j\right)}}.\,$

Bir seri rastsal değişken X₁, ..., X_n ve sabitler 'a₁, ..., an için şu ifade bulunabilir:

$\operatorname{Var}\left(\sum_{i=1}^n a_iX_i \right) = \sum_{i=1}^n a_i^2\operatorname{Var}(X_i) + 2\sum_{i,j\,:\,i<j} a_ia_j\operatorname{Cov}(X_i,X_j).$

Çoklu-değişirli vektör-değişkenleri halleri ve kovaryans matrisi

Eğer X ve Y çoklu-değişirli vektör rastsal değişkenler ise; m-değişirli (yani m-sütunlu) X vektör-değerli rastsal değişken ile n-değişirli (n-sütunlu) vektör değişken Y arasındaki kovaryans matrisi X matris-bekleme değerleri μ=E(X) ve Y matris bekleme değerleri ν=E(Y) ile şöyle tanımlanır:

$\operatorname{Cov}(X, Y) = \operatorname{E}((X-\mu)(Y-\nu)^{\top}) = \operatorname{E}(X Y^{\top}) - \mu \nu^{\top}\,$

Burada "kovaryans matrisi" m-satırlı ve n-sütunlu (m×n) matrisle ifade edilir ve bu matrisin i satırı ve j sütunu şu kovaryansı verir:

Cov(x_i, y_j)

ve burada 'x_i Xin iinci skaler elemanını ve 'y_j Ynin jinci skaler elemanını gösterir. Bu nedenle Cov(X, Y) ve Cov(Y, X) matrisleri birbirlerinin transpozlarıdır.

Bunu Hilbert uzayında inceleyerek daha genelleştirmek mümkündür.

Ayrıca bakınız

• Korelasyon
• Kovaryans fonksiyonu
• Kovaryans matrisi
• Toplam kovaryans yasası
• Otokovaryans
• Kovaryans analizi
• Örneklem ortalaması ve örneklem kovaryansı
• Varyans