Monte Carlo benzetimi

Rastgele üretilen sayılardan faydalanılarak istatistiksel simülasyonlar Monte Carlo metoduyla yapılır. Monte-Carlo Nicholas Constantine Metropolis (1915-1999) tarafından bulunmuştur ve Atom bombasının geliştirildiği Los Alamos Ulusal Labratuvarında, bombanın patlamasından sonra dağılan nötronlara karşı kalkan modellemek için Stanislaw Ulam tarafından günümüze taşınmıştır.

Deney girdileri belirli olmayan, kesin olmayan bir şekilde gelmesi bekleniyorsa ve dağılım bir fonksiyonla hesaplanabilecekse kullanılır. Monte Carlo, rastgele sayıları baz alarak tahmini sistemleri modeller. Hücre Similasyonu, Borsa Modelleri, Dağılım Fonksiyonları, Sayısal Analiz, Doğal olayların simülasyonu, Atom ve Molekül Fiziği, Nükleer Fizik ve Yüksek Enerji Fiziği modellerini test eden simülasyonlar, Deneylerde kullanılan aletlerin simülasyonu (Örneğin bir madde içerisinde x ışınlarının dağılımı).

Yukarıdaki modellerde tahminler yapabilmek için; Rastgele sayı üretilir, bunun için programlama bilgisi gerekmektedir.

1. Programlama: Temel düzeyde Monte Carlo programları öğrenildikten sonra, Monte Carlo üreteçlerini oluşturabilmek gerekmektedir. Teorik eğitimin yanında örneğin C, C++ gibi bilimsel çalışmalarda sıklıkla kullanılan programları iyi derecede bilmek gerekmektedir.
2. Teorik: Programlama aşamasına geçmeden önce problemi ya da deney sistemimizin teorisini çok iyi oluşturmamız gerekmektedir.

Aşağıda Pi sayısının Monte Carlo Yöntemi ile hesaplanması örneği C++ kodları ile verilmiştir.

#include <iostream>
#include <stdlib.h>
#include <time.h> 
using namespace std;
class _pi{
        double pi,x,y;
        double say, atis;
        public:
        void pi_bul();
};

void _pi::pi_bul(){
        say=0.0, atis=10000000;
        cout<<"10000000 icin pi sayisi\n";
        srand((unsigned) time (NULL));
        for (double i=0; i < 10000000 ; i++) {
                x = (double)rand( ) / RAND_MAX;
                y = (double)rand( ) / RAND_MAX;

                if ((x*x) + (y*y)<=1) say++;
        }
        cout<<"pi="<<(double)say/atis*4<<endl;
}

int main(){
        _pi ob;
        ob.pi_bul();
}

Çıktısı:
10000000 icin pi sayisi
pi=3.14132

Monte Carlo Benzetimi, fiziksel ve matematiksel bazı sistemlerin benzetiminde kullanılır. Genelde raslantısal (random) değişkenlerin sisteme etkisinin incelenmesi için kullanılır. Genelde raslantısal değişkenler için rastgele sayılar üreten bir algoritma ile çalışır.

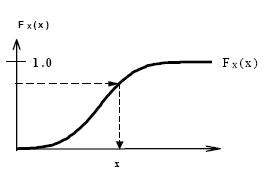
Monte Carlo Benzetimi yapılacak değişkenler belli bir istatistiksel dağılıma uyacak şekilde üretilebilir. Bunun için olasılık dağılım fonksiyonunun (CDF) tersi kullanılır. Bilgisayar tarafından belirli bir aralıkta [0 - 1] düzenli (uniform) olarak üretilen rastgele sayılar olasılık dağılım fonksiyonlarının tersi kullanılarak kolaylıkla herhangi bir dağılıma dönüştürülebilir.

Örneğin iki rassal değişkene (${\displaystyle X_{1}}$, ${\displaystyle X_{2}}$) bağlı olan Y değişkeninin bu değişkenlerle olan ilişkisi f fonksiyonuyla tanımlanmış olsun.

${\displaystyle Y=f(X_{1},X_{2})}$

Eğer ${\displaystyle X_{1}}$ ve ${\displaystyle X_{2}}$ değişkenlerinin dağılımı belliyse (örneğin: Normal Dağılım) ve aynı zamanda dağılım özellikleri de biliniyorsa (μ_x : Ortalama ve σ_x : Standart sapma) X değerleri için defalarca rastgele sayılar üretilerek f fonksiyonuyla Y değerleri hesaplanabilir. Buradan da Y ile ilgili istatistiksel bilgilere ulaşılabilir. Ne kadar çok örnekleme yapılırsa o kadar iyi sonuçlar elde edilir.

Kaynakça

• Bozkaya K: A study on the reliability analysis during preliminary design - A rocket motor example. MS Tez. ODTÜ. Eylül 2006