N-küre hacminin türevi
Geometri'de,bir küre'nin hacmi için bir özel durum n-boyutlu Euclid uzayı içindeki bir kürenin n-boyutlu hacmidir .
n-kürenin hacimlerinin türevleri
Genel form (özyineleme formu)
n-kürenin yarıçapı r. olmak üzere V(n)[r] , n-küre
hacmi
Çünkü bu yarıçapın iki katı uzunlukta düz bir çizgidir i.e.
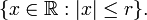
n ≥ 1 için:
ninci kuvvetten yarıçaplı hacim
ninci kuvvetten yarıçaplı n-küre'nin hacmini indüksiyon yoluyla gösterebiliriz .Tek boyutludan yararlanmak n boyutlu çıkarımlar için destek olur:
Buradan:
Biz şimdi bütün n ≥ 1,için ninci kuvvetten yarıçap uzunlukluklu n-kürenin hacmini; birim kürenin hacmini n-kürenin 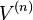 ile gösterirsek:
ile gösterirsek:
İlk birkaç adım
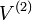 durumunda
durumunda
birim çember bölgesinden,son türevler(çıkarımlar)'la,birim küre hacmi, kolayca:
Genel Durum
Genlleştirilmiş herhangi boyutta bir türevlerini denemek için:
Burada integrandın davranışını grafik yoluyla kolayca görselleştirebiliriz:
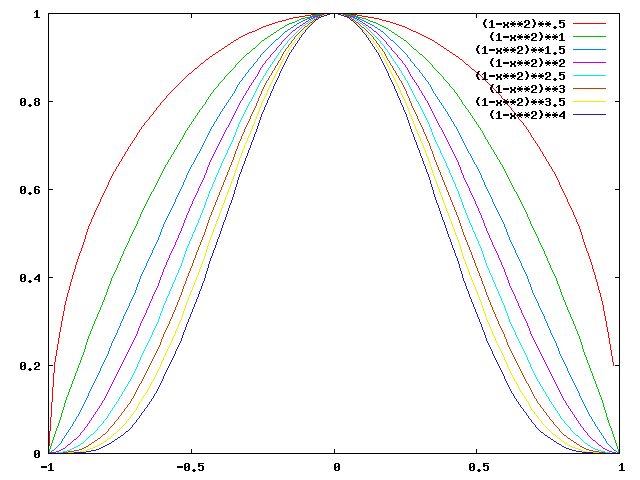
Görüldüğü gibi,hiperküre boyut sayısı arttıkça sıkıştıkça sıkışır.
u değişken değiştirmesi koyarak = 1 − x2 :
integral'in sağı beta fonksiyonu olarak bilinir:
gama fonksiyonu terimleri ilede gösterilebilir:
Bütün l n ≥ 1 için
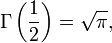 den dolayı induksiyon'la kolayca doğrulanabilir:
den dolayı induksiyon'la kolayca doğrulanabilir:
Genel form ve yüzey alanı
n-kürenin "yüzey alanı" ("n" − 1)-boyutlu (n − 1)-kürenin hacim ölçümü ,n-küre hacimli kürenin yarıçapı ile kolayca bulunabilir .
Bu nedenle n-küre yarıçapı r ile gösterirsek
Buradan "yüzey alanı"
İleri genelleme
p ≠ 2 üzerindeki durumlarda integrasyon metodu,Lp uzay kürelere taşınmalıdır göründüğü gibi sorun pek kolay değil,bu problemin bilgi teorisi ve kodlama teorisi için çok büyük önemi vardır. Nükleer patlamalarda atomaltı kuvvetlerin kuvvetlerin simülasyonunda saçılma kesrinin Çok boyutlu hiperküre hacminin doğru ve titiz hesaplanmasıyla alakalıdır. Ayrıca, başlangıç ifadeler (n) karmaşık analitik sürekli oldukları için boyutsal düzenleme'de ve standart model'de temel parçacıklarla ilgili hesaplamalarda temel bir adım olarak kullanılır.
Kaynakça
bakınız
- n-küre
ileri kaynak
- http://mathworld.wolfram.com/Hypersphere.html
- http://www-staff.lboro.ac.uk/~coael/hypersphere.pdf
- http://www.mathreference.com/ca-int,hsp.html
![V^{(1)}[r]=2r \,](../I/m/21af33fe426700b6e8c7c57f9d1a302a.png)
![V^{(n+1)}[r] = \int_{-r}^r V^{(n)}\left[\sqrt{r^2-x^2}\,\right]\,dx.](../I/m/24101fc7bc5f8f30f7363b549ef934ba.png)
![V^{(n)}[r] = r^nV^{(n)}[1]. \,](../I/m/9c0569d86880d25cf00e38f123ed7e88.png)
![V^{(n+1)}[r] = \int_{-r}^r V^{(n)}\left[\sqrt{r^2-x^2}\,\right] dx,](../I/m/5325d809f0dfa84b9a568a356f17a496.png)
![V^{(n+1)}[r] = r \int_{-1}^1 V^{(n)}\left[\sqrt{r^2-(rx)^2}\,\right] \, dx,](../I/m/d6d1b80d035f6abb3951fb90b00c20ad.png)
![V^{(n+1)}[r] = r \int_{-1}^1 V^{(n)}\left[r\sqrt{(1-x^2)}\,\right] dx,](../I/m/2cdb4a246c540afad5caa5d5389945b3.png)
![V^{(n+1)}[r] = r \int_{-1}^1 r^n V^{(n)}\left[\sqrt{(1-x^2)}\,\right] dx = r^{n+1}V^{(n+1)}[1].](../I/m/0816080823723688725cf2664ecf27c0.png)
![V^{(n)}[r] = r^nV^{(n)}, \,](../I/m/168b835e7e2c4fc6da888ac07c36a4f6.png)
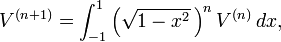
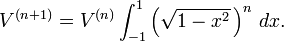
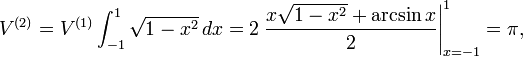
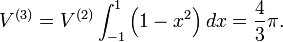
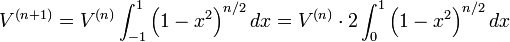
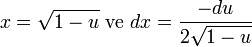
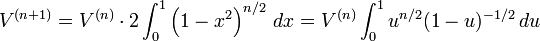
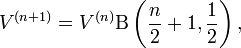
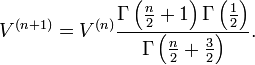
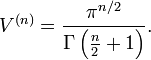
![V^{(n)}[r] = \frac {\pi^{n/2} r^n}{\Gamma\left(\frac n 2 + 1 \right)},](../I/m/681f4f8f88532115c9ad30bce4cb9e86.png)
![S^{(n-1)}[r] = \frac \partial{\partial r} V^{(n)}[r] = \frac {\pi^{n/2} nr^{n-1}}{\Gamma\left(\frac n 2 + 1 \right)}
= \frac {2\pi^{n/2}r^{n-1}}{\Gamma\left( \frac n 2 \right)}.](../I/m/c2b64193c8e15664bfe5f3e8d2d5c101.png)