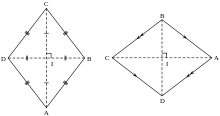
Eşkenar dörtgen

Eşkenar dörtgen

İki eşkenar dörtgen
Tip	dörtgen
Kenarlar ve Köşeler	4
Simetri grubu	D2, [2], (*22)
Alan	${\displaystyle {\tfrac {pq}{2}}}$
Eşlek çokgen	dikdörtgen
Özellikler	konveks, isotoksal

Geometride bir eşkenar dörtgen (baklava dilimi, rhombus veya rombus da denir), dört kenarı eşit uzunlukta bir dörtgendir. Oyun kağıtlarında görülen eşkenar dörtgene karo, bu şekle sahip olan haplara lozanj, bu şekle sahip olan beyzbol oyun sahasına diamond (elmas) denir.

Her eşkenar dörtgen bir paralel kenardır ve dik açılı olanı bir karedir. Öklid'in özgün rhombus tanımı kareyi dışlar ama modern matematikçiler kareyi de kapsayan tanımı tercih ederler.^[1] Rhombus, Eski Yunanca topaç anlamına gelen ῥόμβος (rhombos) sözcüğünden gelir.

Özellikleri

Her eşkenar dörtgende köşeleri birleştiren iki çift paralel kenar ve iki köşegen vardır. Eşleşik (benzer) üçgenler kullanılarak, eşkenar dörtgenin bu köşegenlerin her birine göre simetrik olduğu ispatlanabilir. Dolayısıyla her eşkenar dörtgen aşağıdaki özellikleri taşır:

1. Karşı açılar eşittir.
2. Köşegenler birbirine diktir; yani eşkenar dörtgen bir dikköşegenli dörtgendir.
3. Köşegenler açıortaydır.
4. Köşegenleri birbirini ortalar.

İlk özellik, her eşkenar dörtgenin bir paralelkenar olduğu anlamına gelir. Eşkenar dörtgen dolayısıyla bir paralel kenarın tüm özelliklerine sahiptir: örneğin, karşı kenarlar paraleldir; bitişik açılar bütünlerdir; iki köşegen birbirini ikiye böler; orta noktadan geçen herhangi bir doğru, alanı ikiye böler; ve kenar uzunluklarının karelerinin toplamı köşegenlerin karelerinin toplamına eşittir (yani, ortak kenar uzunluğuna a ve köşegen uzunluklarına d₁ ve d₂ denirse, 4a² = d₁² + d₂²).

Her paralelkenar bir eşkenar dörtgen değildir ama paralel köşegenleri olan her paralelkenar (ikinci özellik) bir eşkenar paralelkenardır. Genelde, (biri bir simetri ekseni olan) birbirine dik köşegenli her dörtgen bir uçurtmadır. Her eşkenar dörtgen bir uçurtmadır ve hem uçurtma hem paralelkenar olan bir dörtgen bir eşkenar dörtgendir.

Eşkenar dörtgen bir teğetsel dörtgendir.^[2] Yani, dört kenarına da teğet olan bir dış teğet çember vardır.

Köken

Öklid'in eşkenar dörtgen için kullandığı rhombus sözcüğü Yunanca fırıldamak anlamına gelen ρέμβω (rhembo) fiilinden türetmiştir.^[3][4] Arşimet, tabanları ortak iki dik huni için "katı rhombus" terimini kullanmıştır.^[5]

Matematikte

• Bir eşkenar dörtgenin çokgen eşleği (dual polygon) bir dikdörtgendir.
• İki boyutlu örgü (latis) tiplerinden biri rombik örgüdür, ortalanmış dikdörtgenel örgü olarak da adlandırılır.
• Birbirinin aynı eşkenar dörtgenler 2 boyultlu düzlemi üç farklı şekilde döşeyebilirler. 60°'li rombus durumunda ayrıca Rombil döşeme de mümkündür.
• Eşkenar dörtgenin üç boyutlu benzerleri arasında ikipiramit (bipiramit) ve ikihuni bulunur

Alan formülleri

Tüm paralelkenarlar gibi, eşkenar dörtgenin alanı, tabanı ile yüksekliğinin çarpımıdır. Taban kenar uzunluğu a, yükseklik h de komşu olmayan iki kenar arasındaki dikey uzaklık olarak tanımlanırsa, alan A:

${\displaystyle A=a\cdot h.}$

Alan, ayrıca, tabanın karesi çarpı açılardan birinin sinüsü:

${\displaystyle A=a^{2}\cdot \sin \alpha =a^{2}\cdot \sin \beta ,}$

veya köşegen uzunlukların çarpımının yarısı:

${\displaystyle A={\frac {AC\cdot BD}{2}},}$

veya yarıçevre uzunluğu çarpı dışteğet çemberin yarıçapı

${\displaystyle A=2a\cdot r.}$

olarak da ifade edilebilir.

Kaynakça

1. Eric W. Weisstein, Square (MathWorld) inclusive usage
2. Eric W. Weisstein, Rhombus (MathWorld)
3. Rhombos, "A Greek-English Lexicon", Liddel and Scott, at Perseus
4. Rhembo, "A Greek-English Lexicon", Liddel and Scott, at Perseus
5. http://www.pballew.net/rhomb.

Dış bağlantılar

• Parallelogram and Rhombus - Animasyonlu ders (Çizim, Çevre, Alan)
• Rhombus tanımı. Math Open Reference enteraktif uygulamacık.
• Rhombus alanı. Math Open Reference enteraktif uygulamacık kullanarak bir rhombusun alanının hesaplamanın üç farklı yolunu gösterir.