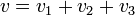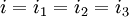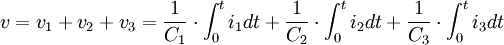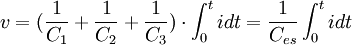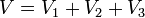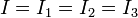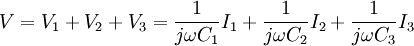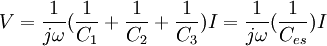Seri bağlama
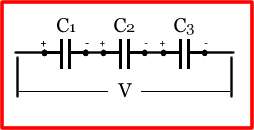
Seri bağlanmış kondansatörler
Elektriksel elemanların seri bağlanmasında önemli olan elemanlarının birbirine bağlı uçlarının işaretidir. Her bir elemanın (-) ucu sonraki kondansatörün (+) ucuna bağlandığında seri bağlama sağlanmış olur. Yandaki resimde düzgün olarak seri bağlanmış 3 adet kondansatör bulunmaktadır. Seri bağlı elemanların her birinden geçen akım aynıdır. Her bir elemanın uçları arasındaki gerilimin toplamı ise o elemanlara uygulanan toplam gerilimi verir.
Kondansatör
Kondansatörler seri bağlandığı zaman, kaynak akımı her bir kondansatörden geçen akıma eşit olur, kaynak gerilimi ise her bir kondansatörün gerilimlerinin toplamı olur.
Zaman domeninde hesap
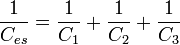 |
Frekans domeninde hesap
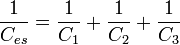 |
This article is issued from Vikipedi - version of the 5/2/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.