Sonlu farklar yöntemi
Sonlu farklar yöntemi bir sayısal yöntemdir. Sonlu fark denklemlerinden faydalanır. Bu denklemler ile diferansiyel denklemlerin analitik çözümlerine yaklaşılır.
Taylor polinomundan türetilişi
n!, n'nin faktöriyelini ve Rn(x) de n. dereceden Taylor polinomu ile asıl fonksiyonun değerleri arasındaki farkı gösteren kalan terimidir. Örnek olarak f fonksiyonunun ilk türevini ele alırsak,
x0 yerine a ve (x-a) yerine h yazarsak,
Tüm terimleri h ile bölersek,
f'(a)'yı yalnız bırakırsak,
- +5154545554545445
Kalan terim göreceli olarak ufak olduğu için aşağıdaki yaklaşıma ulaşırız:
Kesinlik ve mertebe
Yöntemin oluşturduğu hata, söz konusu denklemin gerçek analitik çözümü ile bu gerçek çözüme yapılan yaklaşma (yaklaşık olarak eşit) arasındaki farka eşittir. Sonlu farklar yöntemindeki temel iki hata: yuvarlama hatası ve kesme hatasıdır. Yuvarlama hatası, bilgisayarın ondalık değerleri bir basamaktan sonra yukarı yuvarlamasından oluşur. Yuvarlama hatasına kesinliğin azalması da denebilir. Kesme hatası da, sonlu fark denkleminin gerçek çözümü ile gerçek çözüme yapılan yaklaşım arasındaki farka eşittir (Burada, yuvarlama hatası sıfır kabul edilir.)
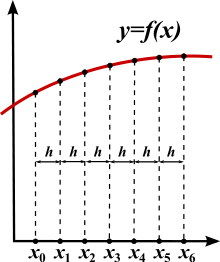
Sonlu farklar yöntemini bir problemi çözmede kullanmak için, önce problemin tanım kümesini ayrıklaştırmak gerekir. Ayrıklaştırma, genelde, tanım kümesini eşit parçalara bölerek yapılır (bir örnek için sağdaki resim).
Yerel kesme hatası