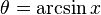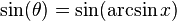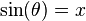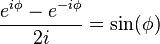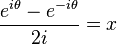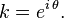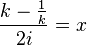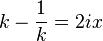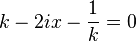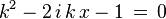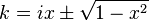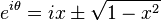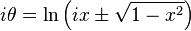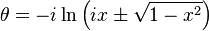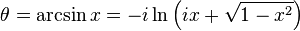Ters trigonometrik fonksiyonlar
Matematikte ters trigonometrik fonksiyonlar, tanım kümesinde bulunan trigonometrik fonksiyonların ters fonksiyonudur.
arcsin, arccos, arctan sırasıyla sin−1, cos−1, tan−1 olarak gösterilir. Fakat bu dönüşüm, sin2(x) gibi yaygın kullanılan ifadelerde karmaşaya neden olabilir. Buradaki sayısal kuvvet, ters çarpan ile ters fonksiyon arasında bir karmaşa meydana getirir.
Bilgisayar programlama dillerinde, arcsin, arccos, arctan fonksiyonları genellikle asin, acos, atan olarak adlandırılır. Çoğu programlama dili de atan2 fonksiyonunu iki argümanlı olarak kullanır ve y / x'in arctanjantını (−π, π] aralığında y ve x olarak ifade eder.
Asıl değerler
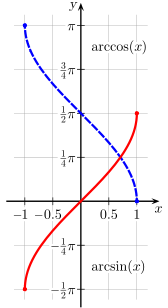
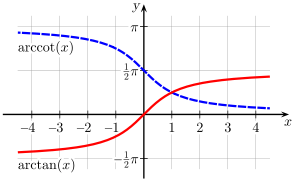
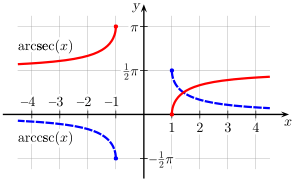
Altı trigonometrik fonksiyondan hiçbiri birebir fonksiyon değildir, terslerinin alınmasında kısıtlamalar vardır. Bu yüzden ters fonksiyonların değerleri, asıl fonksiyonların tanım kümesinin alt kümesidir
Örneğin çok değerli fonksiyonlarda, yalnızca karekök fonksiyonu 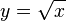 , y2 = x olarak tanımlanabilir. y = arcsin(x) fonksiyonu sin(y) = x olarak ifade edilebilir. sin(y) = x'yi ifade eden birçok y sayısı vardır. Örneğin sin(0) = 0, fakat sin(π) = 0, sin(2π) = 0, vb. arcsin fonksiyonu da çok değerlidir: arcsin(0) = 0, fakat arcsin(0) = π, arcsin(0) = 2π, vb. Yalnızca tek bir değer belirtildiğinde, fonksiyon kısıtlanır. Bu kısıtlama ile, tanım kümesindeki her bir x için arcsin(x) ifadesi yalnızca tek bir değere karşılık gelir, bu da asıl değer olarak adlandırılır. Bu özellikler tüm ters trigonometrik fonksiyonlarda uygulanır.
, y2 = x olarak tanımlanabilir. y = arcsin(x) fonksiyonu sin(y) = x olarak ifade edilebilir. sin(y) = x'yi ifade eden birçok y sayısı vardır. Örneğin sin(0) = 0, fakat sin(π) = 0, sin(2π) = 0, vb. arcsin fonksiyonu da çok değerlidir: arcsin(0) = 0, fakat arcsin(0) = π, arcsin(0) = 2π, vb. Yalnızca tek bir değer belirtildiğinde, fonksiyon kısıtlanır. Bu kısıtlama ile, tanım kümesindeki her bir x için arcsin(x) ifadesi yalnızca tek bir değere karşılık gelir, bu da asıl değer olarak adlandırılır. Bu özellikler tüm ters trigonometrik fonksiyonlarda uygulanır.
Aşağıdaki tabloda ters trigonometrik fonksiyonların asılları listelenmiştir.
| Fonksiyon | Genel gösterim | İfade | x değer aralığı | Asıl değer aralığı (radyan) |
Asıl değer aralığı (derece) |
|---|---|---|---|---|---|
| arcsinüs | y = arcsin x | x = sin y | −1 ≤ x ≤ 1 | −π/2 ≤ y ≤ π/2 | −90° ≤ y ≤ 90° |
| arckosinüs | y = arccos x | x = cos y | −1 ≤ x ≤ 1 | 0 ≤ y ≤ π | 0° ≤ y ≤ 180° |
| arctanjant | y = arctan x | x = tan y | tüm reel sayılar | −π/2 < y < π/2 | −90° < y < 90° |
| arckotanjant | y = arccot x | x = cot y | tüm reel sayılar | 0 < y < π | 0° < y < 180° |
| arcsekant | y = arcsec x | x = sec y | x ≤ −1 or 1 ≤ x | 0 ≤ y < π/2 or π/2 < y ≤ π | 0° ≤ y < 90° or 90° < y ≤ 180° |
| arckosekant | y = arccsc x | x = csc y | x ≤ −1 or 1 ≤ x | −π/2 ≤ y < 0 or 0 < y ≤ π/2 | -90° ≤ y < 0° or 0° < y ≤ 90° |
Eğer x bir karmaşık sayı olursa, y değer aralığı yalnızca gerçel kısımda olur.
Ters trigonometrik fonksiyonların ilişkisi
Negatif argümanlar:
Karşıt argümanlar:
Eğer yalnızca bir sinüs tablosu varsa:
Burada bir karmaşık sayının karekökü kullanılırsa, bunun pozitif gerçel kısmı (veya kare negatif gerçel ise sanal kısım) seçilir.
Tanjant yarım açı formülünden, 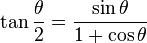 , aşağıdakiler elde edilebilir;
, aşağıdakiler elde edilebilir;
Trigonometrik fonksiyonlar ile ters trigonometrik fonksiyonlar arasındaki ilişkiler
Ters trigonometrik fonksiyonların türevleri
x in reel ve karmaşık değerlerinin türevleri şöyledir:
x in yalnızca reel değerleri şöyledir:
Örnek bir türev: eğer 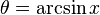 ise;
ise;
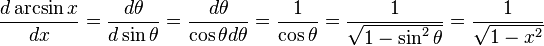 olur.
olur.
Belirli integral olarak ifadesi
Bir noktadaki türevin integrali ve sabit değeri, ters trigonometrik fonksiyonların belirli integrallarinin ifadesini verir:
x 1'e eşit olduğunda, integraller tanım kümesini belirsiz integral ile kısıtlar, fakat yine de iyi tanımlıdırlar.
Sonsuz seriler
Sinüs ve kosinüs gibi fonksiyonların ters trigonometrik fonksiyonları sonsuz seriler kullanılarak hesaplanabilir, şöyle ki:
Leonhard Euler, arctanjant için daha kullanışlı bir seri buldu:
(n = 0 için toplamdaki terimin boş çarpım (ki bu 1'dir) olduğuna dikkat edin.)
Alternatif olarak bu şöyle de ifade edilebilir;
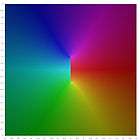
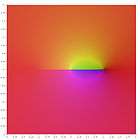
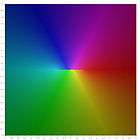
Logaritmik biçimler
Bu logaritmik biçimler karmaşık düzlemde bulunur.
Örnek ispat
Sinüsün üstel biçimi şöyledir;
Böylece ifade şöyle olur:
Burada aşağıdaki gibi bir değişken değiştirme uygulanırsa;
Eşitlik şöyle olur;
(yukarıdaki eşitliğin pozitif kısmı alınırsa)
 |
 |
 |
 |
 |
 |
 |
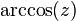 |
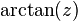 |
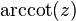 |
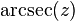 |
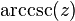 |
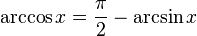
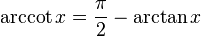
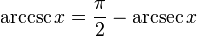
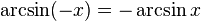
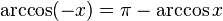
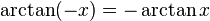
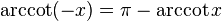
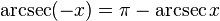
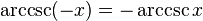
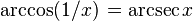
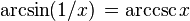
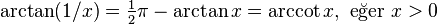
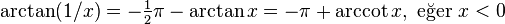
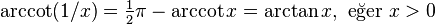
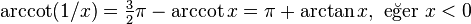
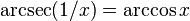
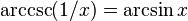
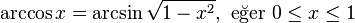
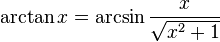
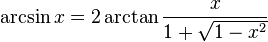
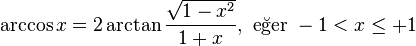
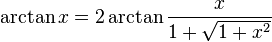
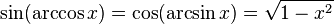
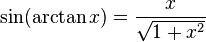
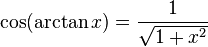
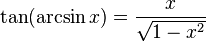
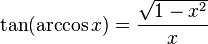
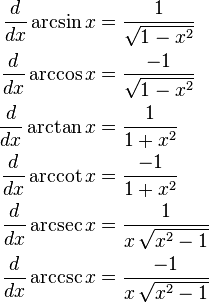
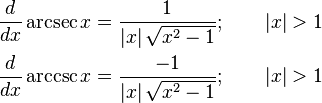
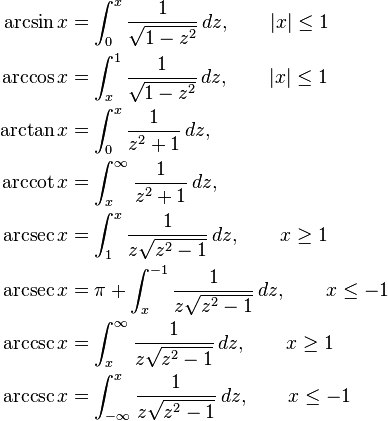
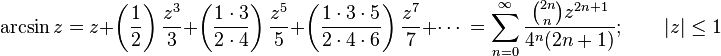
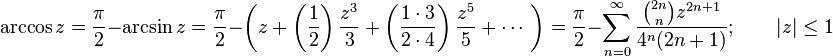
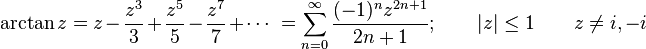
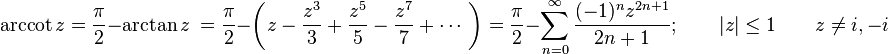
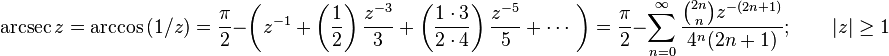
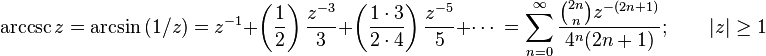
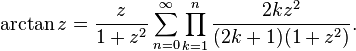
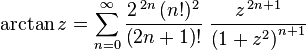
![\begin{align}
\arcsin x &{}= -i\,\ln\left(i\,x+\sqrt{1-x^2}\right) &{}= \arccsc \frac{1}{x}\\[10pt]
\arccos x &{}= -i\,\ln\left(x+i\,\sqrt{1-x^2}\right) = \frac{\pi}{2}\,+i\ln\left(i\,x+\sqrt{1-x^2}\right) = \frac{\pi}{2}-\arcsin x &{}= \arcsec \frac{1}{x}\\[10pt]
\arctan x &{}= \tfrac{1}{2}i\left(\ln\left(1-i\,x\right)-\ln\left(1+i\,x\right)\right) &{}= \arccot \frac{1}{x}\\[10pt]
\arccot x &{}= \tfrac{1}{2}i\left(\ln\left(1-\frac{i}{x}\right)-\ln\left(1+\frac{i}{x}\right)\right) &{}= \arctan \frac{1}{x}\\[10pt]
\arcsec x &{}= -i\,\ln\left(i\,\sqrt{1-\frac{1}{x^2}}+\frac{1}{x}\right) = i\,\ln\left(\sqrt{1-\frac{1}{x^2}}+\frac{i}{x}\right)+\frac{\pi}{2} = \frac{\pi}{2}-\arccsc x &{}= \arccos \frac{1}{x}\\[10pt]
\arccsc x &{}= -i\,\ln\left(\sqrt{1-\frac{1}{x^2}}+\frac{i}{x}\right) &{}= \arcsin \frac{1}{x}
\end{align}](../I/m/044252219bf972cdb8fa84958d0f49c5.png)