Ters fonksiyon

A fonksiyonu ƒ ve tersi ƒ^–1. Çünkü ƒ a yı 3'e götürür, tersi ƒ^–1 3'ü a ya götürür.

Matematikte, ters fonksiyon, bir fonksiyonun görüntü kümesinden alınan herhangi bir elemanını tanım kümesindeki aslına gönderen fonksiyona denir. Bir fonksiyonun tersi, fonksiyon birebir ve örten ise tanımlı olabilir. Ters fonksiyon ${\displaystyle f^{-1}(x)}$ ile gösterilir. Ancak ${\displaystyle f^{-1}(x)}$ yalnızca bir gösterim olup, "f(x) fonksiyonunun çarpmaya göre tersi" ile karıştırılmamalıdır.

Ters Fonksiyon Bulma

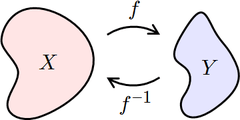
Eğer ƒ X i Y ye götürüyorsa, ƒ^–1 Y yi X e götürür.

• ${\displaystyle f(x)=ax+b}$ şeklindeki doğrusal fonksiyonların tersi ${\displaystyle f^{-1}(x)={\cfrac {x-b}{a}}}$ dır.

Örnek: ${\displaystyle f(x)=3x-2\Rightarrow f^{-1}(x)=f^{-1}(x)={\cfrac {x+2}{3}}}$

• ${\displaystyle f(x)={\cfrac {ax+b}{cx+d}}}$ fonksiyonunun tersi ${\displaystyle f^{-1}(x)={\cfrac {-dx+b}{cx-a}}}$ dır. Bir başka deyişle paydaki x'li terim ile paydadaki sabit sayının hem yerleri hem işaretleri değişir.

Örnek:${\displaystyle f(x)={\cfrac {x+6}{2x-5}}\Rightarrow f^{-1}(x)={\cfrac {5x+6}{2x-1}}}$

• ${\displaystyle f(x)=ax^{2}+bx+c}$ gibi ikinci dereceden polinom şeklindeki fonksiyonların tersini bulmak için şu yol uygulanır;

${\displaystyle f:(3,\infty )\rightarrow (4,\infty )}$

${\displaystyle f(x)=x^{2}-6x+13}$

${\displaystyle y=x^{2}-6x+13}$ (Bu aşamadan sonra x yalnız bırakılmaya çalışılacak.)

${\displaystyle y=(x^{2}-6x+9)+4}$

${\displaystyle y=(x-3)^{2}+4}$ (İfadenin bir kısmı tam kare hâline çevrildi)

${\displaystyle y-4=(x-3)^{2}}$

${\displaystyle {\sqrt {y-4}}={\sqrt {(x-3)^{2}}}}$

${\displaystyle {\sqrt {y-4}}=|x-3|}$

${\displaystyle {\sqrt {y-4}}=x-3}$ (x, 3 ten büyük olduğu için mutlak değer içi pozitiftir.)

${\displaystyle x=3+{\sqrt {y-4}}}$

${\displaystyle f^{-1}(x)=3+{\sqrt {x-4}}}$