Örten fonksiyon

Fonksiyon

x \mapsto f (x)

tanım ve değer kümesine göre

$X$	—›	$B$			$B n$	—›	$B$
$X$	—›	$Z$	—›	$X$
$X$	—›	$R$	—›	$X$	$R n$	—›	$X$
$X$	—›	$C$	—›	$X$	$C n$	—›	$X$

Sınıflar/özellikler

Sabit · Birim · Doğrusal · Polinom · Rasyonel · Cebirsel · Analitik · Yumuşak · Sürekli · Ölçülebilir · Birebir · Örten · Birebir örten

Yapılar

Kısıtlama · Bileşim · λ · Terslik

Genellemeler

Parçalı · Çokdeğerli · Kapalı

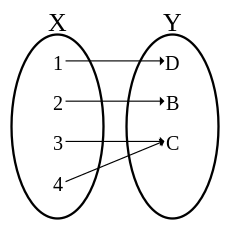
X kümesinden Y kümesine tanımlı örten bir f fonksiyonunun diyagram şeklindeki gösterimi.

Örten fonksiyon, matematikte, X kümesinden Y kümesine tanımlı bir f fonksiyonunda, X kümesindeki her x elemanı için Y kümesindeki y elemanlarının tamamının olduğu fonksiyon türü. Tanım kümesindeki elemanların tamamı, değer kümesindeki elemanların tamamıyla eşleştiği örten fonksiyonlarda, değer kümesi ile görüntü kümesi birbirine eşittir.

Fransızcada "örtenlik" anlamına gelen surjection terimi, injection ("birebirlik") ve bijection ("birebir örtenlik") terimleriyle birlikte Nicolas Bourbaki tarafından ortaya atılmıştır.^[1]

Tanımlama

Örten fonksiyon, tanım kümesindeki elemanların tamamının değer kümesindeki elemanların tamamıyla eşleştiği fonksiyonlardır. Bu durumda fonksiyonun görüntü kümesi, değer kümesine eşit olur.^[2] Fonksiyonun, X tanım kümesindeki her bir x elemanının, Y değer kümesinde en az bir karşılığı vardır ve karşılığı olmayan bir y elemanı bulunmamaktadır. Sembolik olarak bu durum şu şekilde gösterilir:

f\colon X\rightarrow Y

şeklinde tanımlı

f

fonksiyonunun örten olması için

\forall y\in Y,\,\exists x\in X,\;\;f(x)=y

olması gerekmektedir.

Örten fonksiyonlar zaman zaman, sağa bakan iki uçlu ok kullanılarak f : X ↠ Y şeklinde de gösterilebilmektedir.^[3]

Kaynakça

↑ Miller, Jeff (3 Eylül 2016). "Earliest Uses of Some of the Words of Mathematics" (İngilizce). 7 Mayıs 2016 tarihinde kaynağından arşivlendi. http://web.archive.org/web/20160507234812/http://jeff560.tripod.com/i.html.
↑ Vivaldi, Franco (2001) (İngilizce). Experimental Mathematics with Maple. CRC Press. s. 49. ISBN 1584882336. https://books.google.com.tr/books?id=dieHhxLufdcC&pg=PA49&dq=Surjective+function+%22image%22+%22domain%22&hl=tr&sa=X&ved=0ahUKEwjm4pWB9bLRAhWE7hoKHbY0B8YQ6AEIGTAA.
↑ Gorodentsev, Alexey L. (2016) (İngilizce). Algebra I: Textbook for Students of Mathematics. Springer. s. 2. ISBN 3319452851. https://books.google.com.tr/books?id=JcWWDQAAQBAJ&pg=PA2&lpg=PA2&dq=Surjective+function+two+headed+arrow&source=bl&ots=9MkH2StYNf&sig=PZAWNSye7UqQsvhNfLFgL47yruc&hl=tr&sa=X&ved=0ahUKEwio7J6d9LLRAhUJahoKHWPsCdAQ6AEILjAD#v=onepage&q=Surjective%20function%20two%20headed%20arrow&f=false.

This article is issued from Vikipedi - version of the 1/8/2017. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.