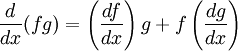Çarpma kuralı
Çarpma kuralı iki veya daha fazla fonksiyonun çarpımının türevinin hesaplanmasında kullanılan bir yöntemdir. Kuralı Gottfried Leibniz türettiği için bu kural Leibniz kuralı olarak da geçer. Kuralın matematiksel ifadesi f ve g sırasıyla f(x) ve g(x) ifadelerinin kapalı formu olmak üzere şöyle verilir:
İspat
Türevin tanımı kullanılarak iki fonksiyonun çarpımının türevine bakılırsa
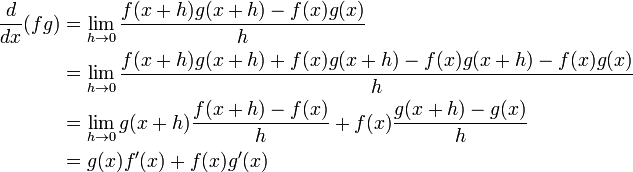
| style="border-bottom: 2px solid #303060"" | Yüksek matematik konuları |
|
Temel Teori |
| Türevleme |
|
Çarpma kuralı |
| İntegral alma |
|
İntegral tablosu |
Genelleme
F fonksiyonu N tane birbirinden farklı ancak aynı değişkene bağlı fonksiyonun çarpımı olsun.
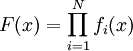
Bu ifadenin türevi yukarda yapılan ispata dayanılarak şu şekilde gösterilir:

Çarpımın ifadesindeki i, 1 'den N 'ye kadar k hariç her değeri alır.