Zincir kuralı
| style="border-bottom: 2px solid #303060"" | Yüksek matematik konuları |
|
Temel Teori |
| Türevleme |
|
Çarpma kuralı |
| İntegral alma |
|
İntegral tablosu |
Zincir kuralı bir değişkene bağlı bir fonksiyonun değişkeninin başka bir değişkene bağlı olması durumunda türevinin:
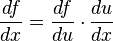 şeklinde yazılabilmesidir [
şeklinde yazılabilmesidir [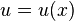 ]. Diğer gösterimleri ise
]. Diğer gösterimleri ise
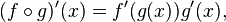 ve
ve
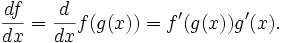 şeklindedir.
şeklindedir.
Örnekler
Örnek A
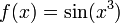 ifadesi
ifadesi 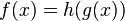 olarak yazılabilir. Burada
olarak yazılabilir. Burada 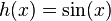 ve
ve 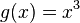 olarak tanımlıdır. Zincir kuralı uygulanırsa f fonksiyonunun türevi:
olarak tanımlıdır. Zincir kuralı uygulanırsa f fonksiyonunun türevi:
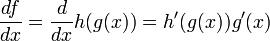 olarak yazılabilir. Türevler yerine koyulursa
olarak yazılabilir. Türevler yerine koyulursa
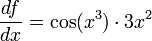 sonucu bulunur.
sonucu bulunur.
Örnek B
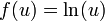 ve
ve 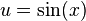 olarak verilsin. f fonksiyonunun x' e göre değişimi zincir kuralı ile
olarak verilsin. f fonksiyonunun x' e göre değişimi zincir kuralı ile
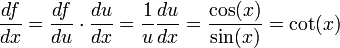 olarak bulunur.
olarak bulunur.