Ölçek değişmezi
Fizik, matematik, istatistik ve ekonomide, ölçek değişmezliği uzunluk, enerji, ya da diğer değişkenlerin ölçülerinin, bir ortak faktör ile çarpılır olup olmadığı değişmez nesneler veya yasaların bir özelliğidir. Bu dönüşüm için teknik terim (ayrıca dilatasyon olarak da bilinir) bir genişleme ve dilatasyon ayrıca daha büyük bir açı korur simetrinin bir parçasını oluşturabilir.
- Matematikte, ölçek değişmezliği genellikle bireysel işlevleri veya eğrilerinin bir değişmezliğini ifade eder. Bir yakın ilişkili kavram, bir fonksiyon ya da eğri dilatasyonları ayrık bir alt kümesi altında değişmezlik kendine benzerlik vardır. Bu rastgele süreçlerin olasılık dağılımları ölçek değişmezliği veya kendine benzerlik bu tür görüntülem için de mümkündür.
- Klasik alan kuramı, ölçek değişmezliği en yaygın dilatasyonların altında bütün bir kuram değişmezliği için de geçerlidir. Bu tür teoriler, tipik karakteristik uzunluk ölçeği ile klasik fizik işlemlerini anlatmaktadır.
- Kuantum alan kuramında, ölçek değişmezliğinin parçacık fiziği açısından bir yorumu vardır. Ölçeği değişmeyen Teorik olarak, parçacık etkileşimlerinin gücü ilgili parçacıkların enerjisine bağımlı değildir.
- Istatistiksel mekanikte, ölçek değişmezliği faz geçişlerinin bir özelliğidir.Anahtar gözlem, bir faz geçişi veya kritik noktası yakınında, dalgalanmalar bütün uzunluk ölçeklerinde oluşabilir ve böylece bir olguyu tanımlamak için açıkça değişmeyen ölçek teorisiyle bakmak gerekir. Bu tür ölçeği değişmez teorilerden istatistiksel alan teorileri vardır, ve resmen kuantum alan teorisi-değişmeyen ölçekli çok benzer.
- Evrensellik çok farklı mikroskobik sistemlerin faz geçişinde aynı davranışı gösterebilir gözlemdir. Birçok farklı sistemlerde böylece faz geçişleri aynı temel değişmeyen ölçek teorisi olarak tarif edilebilir.
- Genel olarak, boyutsuz nicelikler ölçek değişmezdir. istatistiklerde benzer kavram standartlaştırılmamış anlar değil ise , bir değişkenin ölçek değişmez istatistikleri standartlaştırılmış anlar vardır.
Ölçek-değişmez eğriliği ve kendine-benzerlik
matematikte, değişkeninin yeniden ölçeklendirilmesi altında bir fonksiyon veya eğrinin ölçek özellikleri düşünülebilir. Şöyleki bazı ölçek faktörü için ın biçimi içinde ilgilidir,bu bir uzunluk veya yenden ölçeklendirme boyutu olarak alınabilir.Genellikle için gerekli tüm yeniden ölçeklendirme altında değişmez olarak alınmıştır
üstelinin bazı seçimleri ve tüm genişlemeleri, bir homojen fonksiyon olan f için eşdeğerdir.
Ölçek-değişmez fonksiyonların örnekleri tek terimlilerdir, bunun için idi,bu açıklık
içinde
Bir ölçek-değişmez eğrinin bir örneği logaritmik spiraldir, genellikle doğal görünen eğrinin türüdür.polar koordinatların (r, θ) spiral olarak yazılabilir
eğrinin dönmeleri için izin veren, bu tüm yeniden ölçeklendirme altında değişmezdir; bu ve nın bir dönel versiyonu için özdeştir.
İzdüşümsel geometri
Bir tekterimli ölçekli değişmezliği fikri yüksek boyutlarda homojen polinom fikrine ve daha genel olarak bir homojen fonksiyona yaygınlaştırılır. Homojen fonksiyonlar yansıtmalı alan doğal yerlileriyiz ve homojen polinomlar izdüşümsel varyeteler ve izdüşümsel geometri olarak incelenmiştir. Projektif geometri matematiğin özellikle zengin bir alandır; en soyut formlarında, geometrisi şemaları, o string teorisi çeşitli konulara bağlantıları vardır.
Fraktallar
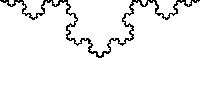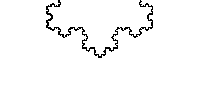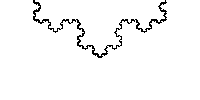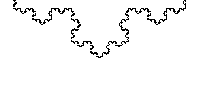
Bazen bu söylenen fraktallar ölçek-değişmezidir, daha kesin olarak , söylemek gerekir ki kendine-benzerdir. Bir fraktal tipik değerler sadece ayrı bir küme için kendisine eşittir, ve daha sonra, fraktalın kendisine bir öteleme ve dönme için eşleşme uygulanmalıdır. Böylece, ölçeği ile Koch eğrisi örneği, ama n tamsayısının değeri için yalnızca ölçek tutar. Buna ek olarak, Koch eğrisinin orijininde sadece ölçekleri değil ,ama, Belli bir anlamda, "her yerde":kendisinin minyatür kopyaları tüm eğrisinin boyunca bulunabilir.
Bazı fraktallarda aynı anda oyunda birden fazla ölçekleme faktörleri olabilir; böyle ölçeklendirmeler çoklu-fraktal analizi ile inceleniyor.
Evrensellik
Evrensellik olarak bilinen bir fenomende fiziksel sistemlerin büyük bir çeşitliliği görülmektedir. Farklı mikroskobi fiziği faz geçişinde aynı ölçekleme davranışına yol açabilir fikrini ifade eder. Evrensellik kurallı bir örnek aşağıdaki iki sistemden oluşur:
Bu iki sistemin Mikroskobik fiziği tamamen farklı olsa bile, kendi kritik üslerinin aynı olduğu ortaya çıkar. Ayrıca, aynı bir istatistiksel alan teorisi kullanarak bu üsleri hesaplayabilirsiniz.Kritik nokta dalgalanmaları bütün uzunluk ölçeklerinde oluşabilir ve böylece bir olguyu tanımlamak ve değişmeyen bir ölçek için istatistiksel alan teorisine bakmalıdır önemli gözlem, bir faz geçişi olup olmadığıdır.Bir anlamda, evrensellik nispeten birkaç tür değişmeyen ölçek teorilerinin olduğu bir gözlemdir.
Aynı ölçek değişmezliği teorisinde anlatılan farklı mikroskobik teoriler kümesi evrensellik sınıfı olarak bilinir. Bir de evrensel sınıfa ait sistemlerinin diğer örnekleri şunlardır:
- Kum yığınlarının çığları.Çığ boyutunun bir çığ olasılığı güç yasası ile orantılıdır ve çığların her büyüklükteki ölçeklerde olduğu görülmektedir.
- Internet üzerindeki ağ kesintisi sıklığı, büyüklüğü ve süresinin bir fonksiyonu olarak.
- Belirli bir yazıda atıfların sayısının bir fonksiyonu olarak, tüm yazılar arasında tüm atıfların ağı dikkate alınarak dergi makaleleri atıfının sıklığı.
- Kağıda taş ve çelik malzemenin içinde çatlak ve yırtıkların oluşumu ve yayılması,yırtılma yönünde ya da bir kırık yüzey pürüzlülüğünün varyasyonları, boyut ölçeği ile güç-kanunu orantılıdır.
- Dielektrikte çatlaklar ve yırtıklara benzeyen elektrik arızası .
- Kırık taş gibi düzensiz bir ortam ya da su yoluyla petrol veya filtre kağıdı gibi kromatografi içinden sıvıların sızması .Güç ölçeklendirme yasası kırıkların dağılımının akış hızına bağlanır.
- Çözümün içinde ve molekülün difüzyonu ve difüzyon ile sınırlı toplamanın bir fenomeni.
- (Yerçekimi kayalar üzerinde hareket ile) sarsılmış olan bir toplama karışımındaki farklı boyutlarda kayaların dağılımı.
Anahtar gözlem bu farklı sistemlerin tümü için, bir faz geçişi tutumuna benzer ve istatistiksel mekanik ve ölçek değişmeyen dili istatistiksel alan teorisi, onları tanımlamak için uygulanabilir olmasıdır.
Ölçek değişmezinin diğer örnekleri
Uygulanan kuvvetin yokluğunda Newtonyen akışkanlar mekaniği
Belirli koşullar altında,, akışkanlar mekaniği bir ölçek değişmez klasik alan teorisidir. alanlar sıvı akışının hızıdır, , sıvı yoğunluğu, , ve sıvı basıncı, . Bu alanlar Navier–Stokes denklemi ve süreklilik denkleminin herikisini karşılamalıdır.Bir Newtonyen akış için bu sıralı formlar alınır
burada dinamik kıvamdır.
Akışkan yoğunluğu için sıvı basıncı ile ölçek değişmezliğini anlamak için bu denklemler özel bir durumun denklemidir, durum denklemi akışkan tipine ve maruz kaldığı koşullara bağlıdır. Örneğin, izotermal, ideal gaz düşünürsek, bunu karşılar
burada sıvıdaki sesin hızıdır. Durumun bu denklemi göz önüne alındığında, Navier-Stokes ve süreklilik denklemi dönüşümler altında değişmez kalmaktadır
verilen çözümleridir ve ,elimizde otomatik olarak var and ayrıca çözümleridir.
Bilgisayarla görme
Bilgisayarla görme, ölçek değişmezliği görüntünün ölçeği değiştiğinde değişmez kalan yerel bir resim açıklaması anlamına gelir. Normalize türev yanıtların ölçekler üzerinden yerel maksimum algılama bu alanda ölçek değişmezliği elde etmek için genel bir çerçeve sağlar. Örnekler uygulamaları ölçek değişmezliği özellik dönüşümü yoluyla damla algılama, sırt algılama ve nesne tanıma içerir
Ayrıca bakınız
- Ölçek göreliliği, fizik
Kaynakça
Daha fazla bilgi
- Zinn-Justin, Jean (2002). Quantum Field Theory and Critical Phenomena. Oxford University Press. Extensive discussion of scale invariance in quantum and statistical field theories, applications to critical phenomena and the epsilon expansion and related topics.
- DiFrancesco, P.; Mathieu, P.; Senechal, D. (1997). Conformal Field Theory. Springer-Verlag.
- Mussardo, G. (2010). Statistical Field Theory. An Introduction to Exactly Solved Models of Statistical Physics. Oxford University Press.