5-hücre

Şablon:Infobox polychoron

Vertex figure: tetrahedron

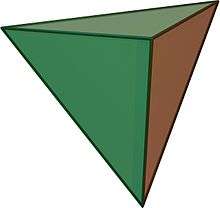
Geometride, 5-hücre 5 dörtyüzlü hücreleri tarafından sınırlanan dört-boyutlu bir nesnesidir. Ayrıca pentakoron, pentatop veya dörtyüzlü hiperpiramid olarak bilinir. Bu 4-simpleks, mümkün olan en basit dışbükey düzenli 4-politop (bir çokyüzlünün dört-boyutlu analogu), ve üç boyutta dörtyüzlü ve iki boyutta üçgen içindedir.

5-hücre düzenli dörtyüzlü ile sınırlanan ve Schläfli sembolü {3,3,3} ile temsil edilen altı düzenli disbükey polikoradan, biridir.

Geometri

5-hücre kendinden-dual, ve onun köşe figürü bir dörtyüzlüdür. 3-boyutlu uzay ile maksimal kesişim üçgen prizmadır. Bu dihedral açı cos-1 (1/4), ya da yaklaşık 75,52 ° 'dir

İnşası

5-hücresi tetrahedron tüm diğer kesişme eşit uzaklıkta olacak şekilde bir 5 köşe ekleyerek tetrahedron inşa edilebilir. (5-hücre aslında bir dörtyüzlü tabanı ile 4-boyutlu bir piramidtir.)

Bir orijin merkezli düzenli 5-hücreli kenar uzunluğu 2 olan köşe Kartezyen koordinatları

${\displaystyle \left({\frac {1}{\sqrt {10}}},\ {\frac {1}{\sqrt {6}}},\ {\frac {1}{\sqrt {3}}},\ \pm 1\right)}$

${\displaystyle \left({\frac {1}{\sqrt {10}}},\ {\frac {1}{\sqrt {6}}},\ {\frac {-2}{\sqrt {3}}},\ 0\right)}$

${\displaystyle \left({\frac {1}{\sqrt {10}}},\ -{\sqrt {\frac {3}{2}}},\ 0,\ 0\right)}$

${\displaystyle \left(-2{\sqrt {\frac {2}{5}}},\ 0,\ 0,\ 0\right)}$

4-Uzay içinde orijin-merkezli koordinatlarının diğer küme kenar uzunluğu 2√2 ile 3-boyutlu uzayda düzenli bir dörtyüzlü tabanı olan bir hiperpiramid olarak :

(1,1,1,-1), (1,-1,-1,-1), (-1,1,-1,-1), (-1,-1,1,-1), (0,0,0,√5 - 1)

Bir 4-simpleks(ile kenarı √2)in köşeleri daha basitçe bir hiperyüzey olarak 5-uzay içinde yapılabilir, (0,0,0,0,1)'ın permütasyonları olarak veya (0,1,1,1,1); in bu pozisyonlar içinde o, sırasıyla, 5-ortopleks veya doğrultulmuş penteraktın bir yönüdür

İzdüşümler

3 boyuta izdüşüm
stereografik izdüşüm tel kafes (kenar üzerine yansıtılan bir 3-küre)	5-hücre gösteriminin bir 3D izdüşümü basit bir rotasyon
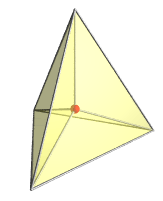3 boyuta pentachoronun  köşe-ilk izdüşümü tetrahedral bir izdüşüm zarf vardır. Burada, kırmızı ile gösterildiği gibi, tetrahedronun merkezine pentachoron izdüşümlerin yakın tepe noktasıdır. tetrahedral zarfın kendisi üzerine uzak hücre izdüşümler iken,4 basık  tetrahedral bölgeler üzerinde diğer 4 hücre izdüşümleri merkezi tepeyi çevreliyor	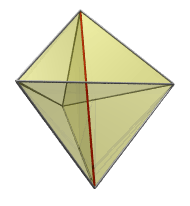3 boyuta pentachoronun kenar- ilk izdüşümü üçgen dipiramidal zarf vardır. (Burada kırmızı ile gösterilen) en yakın kenar bu birbirlerine göre 120 derecelerde bu eksen etrafında düzenlenmiş 3 tetrahedral hacimleri çevreleyen izdüşüm üç hücreler ile, dipiramit eksenine izdüşümdür. Geri kalan 2 hücreleri dipiramitin iki yarısına kadar izdüşüm ve pentatopun uzak tarafında bulunmaktadır.
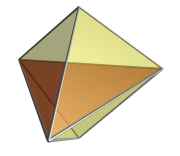3 boyuta pentachoronun yüz yakın izdüşümü aynı zamanda bir üçgen dipiramidal zarf vardır.Yakın yüz burada kırmızıyla gösterilir.Dipiramitin iki yarısına kadar bu yüz izdüşümlerde iki hücreleri buluşur.Kalan üç hücreler 4D açısından pentatopun uzak tarafında, ve netlik için görüntüden çıkarılır. Sadece kenar yakın izdüşüm deki gibi, dipiramitin merkezi ekseni etrafında düzenlenir.	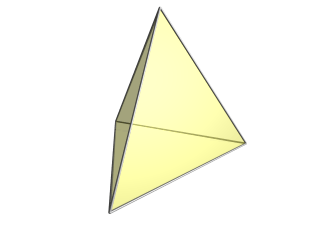3 boyuta pentachoronun hücre-yakın projeksiyonu bir tetrahedral zarf vardır.4D açısından yakın hücre tüm zarfın üzerine izdüşümler, ve, diğer 4 hücreler gizlenmektedir; dolayısıyla, burada işlenmez.

Alternative isimler

• Pentachoron
• 4-simpleks
• Pentatop
• Pentahedroid (Henry Parker Manning)
• Pen (Jonathan Bowers: for pentachoron)
• Hiperpiramid

İlişkili politoplar ve balpeteği

pentachoron (5-hücre) tektip polikoradan basitleştirilerek [3,3,3] Coxeter grubundan yapılmıştır.Şablon:Pentakoron ailesi

Şablon:1 k2 politoplar

Şablon:2 k1 politoplar

O düzenli dizisi içindedir: teserakt {4,3,3}, 120-hücre {5,3,3}, Öklid 4-uzayı, hiperbolik uzayın ve altıgen petek döşeme {6,3,3} . Tüm bu bir dörtyüzlüler bir köşe figürü vardır. Şablon:Dörtyüzlü köşe figürü teselasyonları

O üç regular polychoraya benziyor: tesserakt {4,3,3}, of Öklid 4-uzayının 600-hücre {3,3,5}, ve hiperbolik uzayın yerleşik-6 dörtyüzlü balpeteği {3,3,6}dir. Tüm bu bir dörtyüzlühücrelerde var.Şablon:Dörtyüzlü hücre teselasyonları

Diğer formlar

5-hücre bir dörtyüzlü piramid olarak düşünülebilir, bir tepe noktası hiperyüzey üzerinde ve bir 3-uzay hiperyüzey içinde bir dörtyüzlü olarak taban inşa edilebilir .Dört yan piramidin dörtyüzlü hücrelerinin yapımıdır.

Kaynakça

• T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
• H.S.M. Coxeter:
  • Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
  • H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973, p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
  • Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
    • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
    • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26. pp. 409: Hemicubes: 1_n1)
• Norman Johnson Uniform Polytopes, Manuscript (1991)
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)

Dış bağlantılar

• Eric W. Weisstein, Pentatope (MathWorld)
• Şablon:GlossaryForHyperspace
  • Şablon:PolyCell
• Şablon:KlitzingPolytopes
• Der 5-Zeller (5-cell) Marco Möller's Regular polytopes in R⁴ (German)
• Jonathan Bowers, Regular polychora
• Java3D Applets

Şablon:4D regular polytopes Şablon:Polytopes