Dört yüzlü

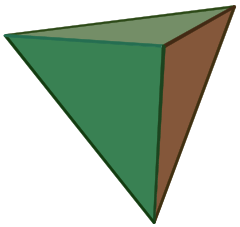
Düzgün Tetrahedron
(Dönen model animasyonu için burayı tıklayınız)
Tip	Platonik cisim
Elemanlar	F = 4, E = 6 V = 4 (χ = 2)
Yüzler	4{3}
Schläfli sembolü	{3,3} and s{2,2}
Wythoff sembolü	3 | 2 3 | 2 2 2
Coxeter-Dynkin
Simetri	Td veya (*332)
Kaynakça	U01, C15, W1
Özellikler	Düzgün konveks deltahedron
Dihedral açı	70.528779° = arccos(1/3)
3.3.3 (Köşesel şekil)	[[{{{T-çifteş}}}]] (çifteş çokyüzlü)
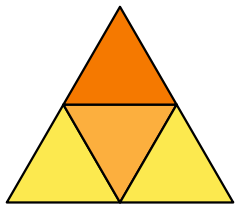Ağ

Geometride tetrahedron veya dörtyüzlü, dört üçgen yüzden oluşan bir çokyüzlüdür (polihedron), her köşesinde üç üçgen birleşir. Düzgün dörtyüzlü dört üçgenin eşkenar olduğu bir dörtyüzlüdür ve Platonik cisimlerden biridir. Dörtyüzlü, dört yüzü olan tek konveks çokyüzlüdür.^[1] Tetrahedron isminin sıfat hali (tetrahedrona ait veya tetrahedronla ilişkili anlamında) "tetrahedral"dir.

Dörtyüzlü, simpleks kavramının üç boyutlu hâlidir.

Dörtyüzlü, bir cins piramittir. Piramit, çokgen bir tabanı tek bir noktada birleştiren üçgen yüzlerden oluşur. Dörtyüzlü durumunda taban bir üçgendir (dört yüzün herhangi biri taban sayılabilir), dolayısıyla dörtyüzlü ayrıca üçgen piramit olarak da bilinir.

Tüm dışbükey (konveks) çokgenler gibi, dörtyüzlü de tek bir kağıt yaprağın katlanması ile meydana gelebilir. İki ağdan oluşur.^[1]

Her bir dörtyüzlü için öyle bir küre (çevrel küre) vardır ki dörtyüzlünün köşeleri bu kürenin yüzeyinde yer alırlar.

Düzgün dörtyüzlüler için formüller

Kenar uzunluğu $a$ olan bir düzgün dörtyüzlü için:

Taban yüzeyin yüzölçümü	${\displaystyle A_{0}={{\sqrt {3}} \over 4}a^{2}\,}$
yüzölçüm[2]	${\displaystyle A=4\,A_{0}={\sqrt {3}}a^{2}\,}$
Yükseklik[3]	${\displaystyle {\sqrt {2 \over 3}}\,a\,}$
Hacim[2]	${\displaystyle V={1 \over 3}A_{0}h={{\sqrt {2}} \over 12}a^{3}\,}$
Bir kenar ile bir yüz arasıdaki açı	${\displaystyle \arccos \left({1 \over {\sqrt {3}}}\right)=\arctan({\sqrt {2}})\,}$ (yaklaşık 54.7356°)
İki yüz arasındaki açı[2]	${\displaystyle \arccos \left({1 \over 3}\right)=\arctan(2{\sqrt {2}})\,}$ (yaklaşık 70.5288°)
Merkezi köşelere birleştiren doğrular arasındaki açı	${\displaystyle \arccos \left({-1 \over 3}\right)=2\arctan({\sqrt {2}})\,}$ (yaklaşık 109.4712°)
Karşısında bir yüz olan bir köşedeki katı açı	${\displaystyle 3\arccos \left({1 \over 3}\right)-\pi \,}$ (yaklaşık 0.55129 steradian)
Çevrel kürenin yarıçapı[2]	${\displaystyle R={\sqrt {3 \over 8}}\,a\,}$
Yüzlere teğet olan içkürenin yarıçapı[2]	${\displaystyle r={1 \over 3}R={a \over {\sqrt {24}}}\,}$
Kenarlara teğet olan ortakürenin yarıçapı[2]	${\displaystyle r_{M}={\sqrt {rR}}={a \over {\sqrt {8}}}\,}$
Dışkürelerin yarıçapları	${\displaystyle r_{E}={a \over {\sqrt {6}}}\,}$
Bir köşeden dışküre merkezine uzaklık	${\displaystyle {\sqrt {3 \over 2}}\,a\,}$

Taban yüze göre bir yüzün eğimi, bir kenarın eğiminin iki katıdır, çünkü taban üzerinde, bir kenar boyunca köşeye olan yatay uzaklık, bir yüzün kenarortayından o köşeye olan uzaklığın iki katıdır. Bir diğer deyişle, eğer C, tabanın ağırlık merkezi (ortacı) ise, C'den tabanın köşelerinden birine olan uzaklık, C'den taban kenarlarından birinin orta noktasına olan uzaklığın iki katıdır. Bunun nedeni, kenarortayların birbirini kütle merkezinde kesmeleri ve bu noktanın her bir kenarortayı uzunlukları 1:2 oranlı olan iki parçaya bölmesidir.

Hacim

Dörtyüzlünün hacmi, piramit hacim formülüdür:

${\displaystyle V={\frac {1}{3}}A_{0}\,h\,}$

burada ${\displaystyle A_{0}}$ tabanın alanı ve h tabandan tepeye olan yüksekliktir. Bu formül her yüz için geçerlidir, dolayısıyla köşelerden karşı yüzlere olan uzaklık, o yüzün alanı ile ters orantılıdır.

Aşağıdaki köşelere sahip bir dörtyüzlü için a = (a₁, a₂, a₃), b = (b₁, b₂, b₃), c = (c₁, c₂, c₃), ve d = (d₁, d₂, d₃), hacim (1/6)·|det(a−b, b−c, c−d)|. Birbirleriyle basit bir çizge oluşturan köşe çiftlerinin herhangi bir diğer kombinasyonu ile de hacmi veren bir formül oluşturulabilir. Bu formül, nokta çarpım ve çapraz çarpım kullanılarak da yazılabilir:

${\displaystyle V={\frac {|(\mathbf {a} -\mathbf {d} )\cdot ((\mathbf {b} -\mathbf {d} )\times (\mathbf {c} -\mathbf {d} ))|}{6}}.}$

Eğer koordinat sisteminin orijini d köşesine rastlayacak şekilde seçilirse, d = 0 olur, dolayısıyla

${\displaystyle V={\frac {|\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )|}{6}},}$

burada a, b ve c bir köşede kesişen üç kenara karşılık gelir ve ${\displaystyle \mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )}$ bir üçlü skaler çarpımdır. Bu formülü bir paralelyüzün hacmi ile karşılıştırınca bir dörtyüzlünün hacminin, onunla üç kesişen yüz paylaşan bir paralelyüzün hacminin 1/6'sı olduğu sonucuna varabiliriz.

Üçlü skaler çarpım aşağıdaki determinantla gösterilebilir:

${\displaystyle 6\cdot V={\begin{vmatrix}\mathbf {a} &\mathbf {b} &\mathbf {c} \end{vmatrix}}}$    veya    ${\displaystyle 6\cdot V={\begin{vmatrix}\mathbf {a} \\\mathbf {b} \\\mathbf {c} \end{vmatrix}}}$    burada    ${\displaystyle \mathbf {a} =(a_{1},a_{2},a_{3})\,}$    satır veya sütun vektör olarak gösterilebilir

Dolayısıyla

${\displaystyle 36\cdot V^{2}={\begin{vmatrix}\mathbf {a^{2}} &\mathbf {a} \cdot \mathbf {b} &\mathbf {a} \cdot \mathbf {c} \\\mathbf {a} \cdot \mathbf {b} &\mathbf {b^{2}} &\mathbf {b} \cdot \mathbf {c} \\\mathbf {a} \cdot \mathbf {c} &\mathbf {b} \cdot \mathbf {c} &\mathbf {c^{2}} \end{vmatrix}}}$    burada    ${\displaystyle \mathbf {a} \cdot \mathbf {b} =ab\cos {\gamma }}$    vb.

bunun sonucu

${\displaystyle V={\frac {abc}{6}}{\sqrt {1+2\cos {\alpha }\cos {\beta }\cos {\gamma }-\cos ^{2}{\alpha }-\cos ^{2}{\beta }-\cos ^{2}{\gamma }}}\,}$,

burada ${\displaystyle \alpha ,\beta ,\gamma \,}$, d köşesinde oluşan düzlemsel açılardır. ${\displaystyle \alpha \,}$ açısı, d köşesini b ve c köşelerine bağlayan kenarlar arasındaki açıdır. ${\displaystyle \beta \,}$ açısı a ve c köşeleri için aynı şeyi yapar, ${\displaystyle \gamma \,}$ de a ve b köşelerinin konumları ile tanımlanmıştır. Dörtyüzlünün köşeleri arasındaki uzaklıklar kullanılarak hacim hesaplamak için Cayley–Menger determinantı kullanılır:

${\displaystyle 288\cdot V^{2}={\begin{vmatrix}0&1&1&1&1\\1&0&d_{12}^{2}&d_{13}^{2}&d_{14}^{2}\\1&d_{12}^{2}&0&d_{23}^{2}&d_{24}^{2}\\1&d_{13}^{2}&d_{23}^{2}&0&d_{34}^{2}\\1&d_{14}^{2}&d_{24}^{2}&d_{34}^{2}&0\end{vmatrix}}}$

burada ${\displaystyle i,\,j\in \{1,\,2,\,3,\,4\}}$ indisleri ${\displaystyle \{\mathbf {a} ,\mathbf {b} ,\mathbf {c} ,\mathbf {d} \}}$ köşelerini temsil eder ve ${\displaystyle d_{ij}\,}$ bunlar arasındaki ikili uzaklıklardır, yani iki köşeyi birleştiren kenarın uzunluğu. Determinantın negatif değerli olması, verilen uzunluklara sahip bir dörtyüzlünün olamayacağı anlamına gelir. Bu formül, bazen Tartaglia formülü olarak da bilinir, 15. yüzyılda yaşamış ressam Piero della Francesca'dan kaynaklanır. Bir üçgenin alanını hesaplamakta kullanılan, 1. yüzyılda keşfedilmiş Heron formülü'nün üç boyuttaki karşılığıdır.^[4]

Kenarlar arasındaki uzaklık

Dörtyüzlünün iki karşı kenarı, iki aykırı doğru üzerinde yer alırlar (aykırı doğrular birbirlerine ne paralel ne de birbirini kesen doğrulardır). Bu iki doğru arasındaki en yakın noktalar kenarlara ait noktalarsa bu noktalar kenarlar arasındaki en yakın uzaklığı tanımlar; aksi halde, kenarlar arasındaki uzaklık, uç noktalar ve karşı kenar arasındaki uzaklıklardan en kısa olanıdır. a ve b-c karşı kenarlarının oluşturduğu aykırı doğrular arasındaki uzaklık ${\displaystyle d}$ olsun.^[5] Bu durumda hacim için bir diğer formül şöyledir:

${\displaystyle V={\frac {d|(\mathbf {a} \times \mathbf {(b-c)} )|}{6}}.}$

Geometrik ilişkiler

Dörtyüzlü ilüstrasyonu, yapısını vurgulamak için dört farklı yöntem kullanılmıştır: çevirme, katlanma/katlanmama, yarı şeffaflık ve En önemlisi stereogram. (50–70 cm tam çözünürlükte izlenmesi önerilir)
Animasyonu izle

Dörtyüzlü bir 3-simpleks'tir. Diğer Platonik cisimlerden farklı olarak, bir düzgün dörtyüzlünün tüm köşeleri birbirinden eşit uzaklıktadır. Köşeler, üç boyutlu uzayda dört noktanın birbirine eşit uzaklıkta olabileceği tek konumdadır.

Dörtyüzlü, üçgensel bir piramittir. Düzgün dörtyüzlü öz-çifteştir (İng. self-dual).

Düzgün bir dörtyüzlü bir küpün içine iki farklı şekilde yerleştirilebilir, her köşe küpün bir köşesi ve her kenar küpün yüzlerinden birinin çaprazı olacak şekilde. Bu yerleştirmelerden biri için, köşelerin koordinatları şöyledir:

(+1, +1, +1);

(−1, −1, +1);

(−1, +1, −1);

(+1, −1, −1).

Meydana gelen bu dörtyüzlünün orijin merkezli olup kenar uzunluğu 2√2'dir. Öbür dörtyüzlü (birincisinin öz-çifteşidir) için tüm işaretlerin tersini alın. Bu iki dörtyüzlünün köşeleri birlikte küpün köşelerini meydana getirirler. Böylece bir düzgün dörtyüzlünün bir 3-yarıküpü (3-demicube) olduğu gösterilmiş olur.

yıldızlaşmış sekizyüzlü (Stella octangula).

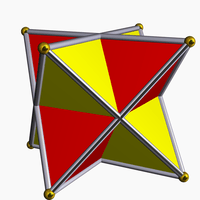
Bu dörtyüzlünün hacmi kübün hacminin 1/3'üdür. İki dörtyüzlüyü birleştirince bir birleşik çokyüzlü (aynı merkeze sahip birden çok çokyüzlü) oluşur, bunun adı iki dörtyüzlü bileşimi (compound of two tetrahedra) veya yıldızlaşmış sekizyüzlü (stellated octahedron)'dur.

Yıldızlaşmış sekizyüzlünün içi bir sekizyüzlüdür. Dolayısıyla, düzgün bir dörtyüzlüden yarım kenar uzunluğunda dört tane düzgün dörtyüzlü kesilmesinin sonucu, düzgün bir sekizyüzlüdür. Bu işleme dörtyüzlünün rektifikasyonu denir.

Küpün içine bir dörtyüzlü yerleştirince beş dörtyüzlü meydana gelir, bunlardan biri düzgündür. Bir küpü oluşturmak için gereken dörtyüzlü sayısı en az 5'tir.

Düzgün çokyüzlüler uzayı karolayamazlar. Bunun olabileceği o kadar makul görünmüştür ki Aristo bunun olabileceğini iddia etmiştir. Ancak, iki düzgün dörtyüzlü ve bir sekizyüzlü ile birleştirilerek bir eşaltıyüzlü (rhombohedron) oluşur, bununla uzay karolanabilir.

Ancak, uzayın karolayabilen en az bir düzensiz dörtyüzlü vardır. Dörtyüzlülerin hepsinin aynı boyda olması şartı esnetilirse, sadece dörtyüzlüler kullanarak uzayı kaplamak mümkündür. Örneğin bir sekizyüzlüyü dört döryüzlüye bölüp bunları iki düzgün dörtyüzlü ile birleştirilebilir (bu iki tip dörtyüzlünün hacimleri eşittir).

Düzgün çokyüzlüler arasında paralel yüzlere sahip olmayan tek cisim dörtyüzlüdür.

İlgili çokyüzlüler

• 
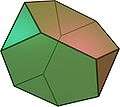  Kesik dörtyüzlü
• 
  bir küp içinde iki dörtyüzlü
• 
  Beş dörtyüzlü bileşimi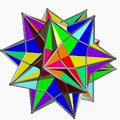
• 
  On dörtyüzlü bileşimi

Bir dörtyüzlüye uygulanacak bir kesme işlemi düzgün bir çokyüzlüler serisi meydana getirir. Kalan kenarları nokta haline getirecek şekilde kesmek, rektifiye bir dörtyüzlü olan bir sekizyüzlü oluşturur. Bu işlem devam ettirilirse sonunda ikili rektifikasyon (birectification) olur, başlangıçtaki yüzler birer noktaya indirgenir, ve öz-çifteş dörtyüzlü yeni baştan ortaya çıkar.

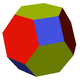
Ad	dörtyüzlü	rektifiye dörtyüzlü (sekizyüzlü)	kesik dörtyüzlü	cantellated tetrahedron (küpsekizyüzlü)	omnitruncated tetrahedron (kesik sekizyüzlü)	Snub tetrahedron (yirmiyüzlü)
Schläfli	{3,3}	t1{3,3}	t0,1{3,3}	t0,2{3,3}	t0,1,2{3,3}	s{3,3}
Coxeter-Dynkin
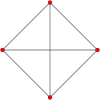
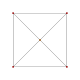
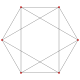
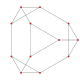
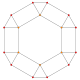
Çizge (A3)
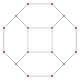Çizge (A2)
Katı
Karolama

Kesişen dörtyüzlüler

Kesişen beş tane dörtyüzlü ile ilginç bir çokyüzlü inşa edilebilir. Beş tane dörtlüden oluşan bu bileşik yüzyıllardır bilinmektedir. Origamide sık sık görülür. 20 köşenin birleştirilmesi ile bir dodekahedron (yirmiyüzlü) meydana gelir. Birbirinin ayna görüntüsü olan sağ elli ve sol elli biçimleri vardır.

Izometri

Düzgün dörtyüzlerde izometriler

Düzgün dörtyüzlülerin simetri grubunda dönme ve yansımalar

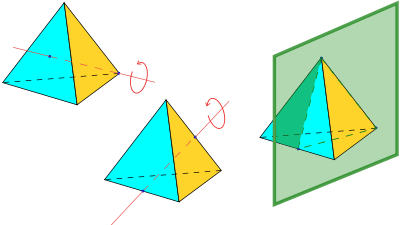
Bir küpün köşeleri, her biri bir dörtyüzlü oluşturan, dörtlü iki gruba ayrılabilir (bkz. yukarısı, ve ayrıca animasyon). Düzgün bir dörtyüzlünün simetrileri bir kübün simetrilerinin yarısına karşılık gelir: dörtyüzlüleri kendilerine dönüştürenler ve birbirine dönüştürmeyenler.

Dörtyüzlü, platonik cisimler arasında noktasal yansıma ile kendi kendine rastlamayan tek cisimdir.

Düzgün dörtyüzlünün 24 izometrisi vardır, T_d simetri grubu ve ona eşbiçimli(izomorfik) olan S₄ oluşturur. Bunlar şöyle kategorilendirilebilir:

• T, A₄ almaşık grubu (özdeşlik ve 11 dönme işlemi) ile izomorfiktir, aşağıdaki eşlenik sınıfları vardır (parantez içinde köşelerin permutasyonları ve birim kuaterniyon gösterimleri verilmiştir):
  • özdeşlik
  • bir köşeden geçen ve karşı yüze dik bir eksen etrafında ±120° dönme: 4 eksen, eksen başına 2, birlikte 8 ((1 2 3), vb.; (1 ± i ± j ± k)/2)
  • 180° bir açıyla dönme öyleki kenar karşı kenar ile çakışsın. 3 ((1 2)(3 4), vb.; i, j, k)
• bir kenara dik bir düzlemde yansıma: 6
• bir düzlemde yansıma ile o düzleme dik bir eksen etrafında 90° dönme: 3 eksen, eksen başına 2, birlikte 6; buna eşdeğer olarak, 90° dönmelerle ters dönmeler (x'in −x'e dönüşmesi) birleşimidir: dönmeler bir küpte bir yüzü öbür yüze dönüştüren dönmelere karşılık gelir.

Düzensiz dörtyüzlülerin izometrileri

Düzensiz bir dörtyüzlünün izometrileri (eşölçer dönüşümleri) dörtyüzlünün geometrisine bağlıdır, 7 durum olabilir. Her durumda bir 3-boyutlu noktalar kümesi meydana gelir.

• Eşkenar üçgen bir taban ve (eşkenar olmayan) ikizkenar üçgen kenarlar durumunda 6 izometri vardır, bunlara tabanın 6 izometrisine karşılık gelir. Köşelerin permutasyonlarına karşılık gelen bu 6 izometri şunlardır: özdeşlik 1, (123), (132), (12), (13) ve (23). Bunlar S₃ ile izomorfik olan C_3vsimetri grubunu oluşturur.
• Dört (eşkenar olmayan) ikizkenar üçgen 8 izometri verir. Eğer (1,2) ve (3,4) kenarları diğer dört kenradan farklı uzunluktaysa bu 8 izometri şunlardır: özdeşlik 1, yansımalar (12) ve (34), ve 180° dönmeler (12)(34), (13)(24), (14)(23) ve 90° dönmeleri (1234) and (1432). Bunlar D_2d simetir grubunu oluşturur.
• Dört çeşitlenar üçgen 4 izometri verir. İzometriler şunlardır: 1 ve 180° dönmeleri (12)(34), (13)(24) ve (14)(23). Bu, Klein dört-kümesi V₄ ≅ Z₂² (nokta kümesi D₂ olan).
• İki çift izomorfik (eşkenar olmayan) ikizkenar üçgen. Birbirine dik ve farklı uzunlukta (1,2) and (3,4) kenarları vardır. 4 izometeriler şunlardır: 1, yansıma (12) ve (34) ve 180° dönmeleri (12)(34). Simetri grubu C_2v'dır, V₄'e izomorfiktir.
• İki çift izomofik çeşitkenar üçgen. İki çift eşit uzunluklu kenar vardır (1,3), (2,4) ve (1,4), (2,3) ama bunlar dışında hiçbir kenar eşit değildir. Olan izometriler 1 ve (12)(34) dönmesidir. Simetri grubu C₂'dır, Z₂'e izomorfiktir.
• Ortak kenarlı iki farklı eşkenar üçgen. İki çift eşit uzunluklu kenarlar vardır (1,3), (1,4) ve (2,3), (2,4), ama bunlar dışında hiçbir kenar eşit değildir. Olan izometriler 1 ve (34) yansımasıdır. Simetri grubu C_s'dır, Z₂'e izomorfiktir.
• Hiçbir kenar birbirine eşit değildir, tek izometri özdeşliktir ve simetri grubu trivial gruptur.

Dörtyüzlüler için sinüsler kanunu ve tüm dörtyüzlü şekillerinin uzayı

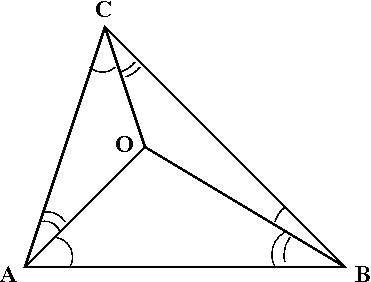
Sinüs teoreminin bir sonucu olarak, köşeleri O, A, B, C olan bir dörtyüzlüde

${\displaystyle \sin \angle OAB\cdot \sin \angle OBC\cdot \sin \angle OCA=\sin \angle OAC\cdot \sin \angle OCB\cdot \sin \angle OBA.\,}$

Bu eşitliğin iki tarafı, yüzlerin saat yönlü ve ters saat yönlü okunuşu gibi düşünülebilir.

Dört köşeden her birini O köşesi yerine koymak buna benzer dört eşitlik yaratır, ama bunların en fazla üç tanesi bağımsızdır: eğer eşitliklerin "saat yönlü" tarafları birbiriyle çarpılırsa, sonucun "ters saat yönlü" tarafların çarpımına eşit olduğu çıkarımı yapılabilir. Her iki taraftaki ortak çarpanlar atılırsa geriye kalan, dördüncü eşitliktir. Bu "bağımsızlık" ilişkisinin önemli olmasının bir nedeni şudur: üç açının bir üçgene ait olması için toplamlarının yarım çembere (180°) eşit olması gerekir. 12 açı için hangi şart bunların bir dörtyüzlüye ait olmasını sağlar? Dörtyüzlünün her bir yüzündeki açıların toplamı yarım çemberdir. Bu şekilde dört üçgen olduğuna göre açı toplamlarına etki eden dört kısıt vardır. Dolayısıyla serbestlik derecesi 12'den 8'e düşer. Bu sinüs teoreminindeki dört ilişki, serbestlik derecelerini 8'den 4'e değil, 5'e indirir, çünkü dördüncü kısıt ilk üçten bağımsız değildir. Dolayısıyla olasıl tüm dörtyüzlülerin oluşturduğu açı değerlerinin uzayı 5 boyutludur.

Uygulamalar

Ammonium+ iyonu dörtyüzlüdür

Dörtyüzlü zar

Dört yüzlü bir ışık cismi, Martina Schettina, Avusturya

Sayısal analiz

Sayısal analizde, özellikle kısmi diferansiyel denklemlerin sayısal çözümlerinde, sonlu eleman analizi için denklemler kurarken, karmaşık üç boyutlu şekiller çoğu zaman düzensiz dörtyüzlülerden oluşan bir çokgen ağ ile yaklaşıklanır. Bu yöntemler çeşitli mühendislik dallarında yaygın olarak kullanılmaktadır.

Kimya

Kimyada kuaterner faz diyagramları grafik olarak tetrahedron olarak gösterilir. (Ancak, iletişim mühendisliğinde kuaterner faz diyagramları grafik olarak iki boyutlu gösterilir.)

Elektrik ve elektronik

Eğer dört eşit rezistör birbirine bağlanarak bir tetrahedron oluşturursa, iki köşe arasındaki direnç, bir rezistörün direncinin yarısı kadardır.^[6]

Oyun

Özellikle rol oyunlarında dört-yüzlü zar sık kullanılır. Atılan sayı ya tabanın etrafında ya da üst köşede yazılı olur.

Bazı Rubik Küpü-benzeri bulmacalar dörtyüzlüdür, örneğin Pyraminx ve Pyramorphix.

Renk uzayı

Renk uzayı dönüşüm algoritmalarında, özellikle lüminans ekseni renk uzayını çapraz kestiği durumlarda (örneğin RGB, CMY), tetrahedral interpolasyon kullanılır.^[7]

Jeoloji

William Lowthian Green tarafından ilk yayımlanan ve Dünyanın oluşumunu açıklamak için^[8] öne sürülen tetrahedral hypotez, 20. yüzyılın başlarında popülerdi.^[9][10]

Doğada

Kimya

Dörtyüzlü (tetrahedron) şekli, moleküllerin kovalent bağlarında görülür. sp³-hibritlenmiş atomlara çevreleyen atomlar bir dörtyüzlünün köşelerinde yer alır, yani tetrahedral moleküler geometriye sahiptir. Örneğin, bir metan molekülü (CH₄) veya bir amonyak iyonunda (NH₄⁺), merkezdeki karbon veya azot atomu, tetrahedral simetriye sahip dört hidrojen atomu ile çevrilidir. Bu yüzden organik kimyanın önde gelen dergilerinden biri Tetrahedron olarak adlandırılmıştır.

Düzgün bir dörtyüzlünün iki köşesi arasındaki merkez açı θ = ${\displaystyle \arccos {\left(-{\tfrac {1}{3}}\right)}}$, veya yaklaşık 109.47°'dir.

Elektronikte kullanılan en yaygın yarı iletken olan silikonun değerlik sayısı dörttür. Silikon atomunun bağlarının tetrahedral şekli, silikon kristallerinin oluşumunu ve şekillerini belirler.

Kaynakça

1. Eric W. Weisstein, Tetrahedron (MathWorld)
2. Coxeter, H. S. M.: Regular Polytopes (Methuen and Co., 1948). Table I(i).
3. "Tetrahedron". 30 Mayıs 2015 tarihinde kaynağından arşivlendi. http://web.archive.org/web/20150530173116/http://www.mathematische-basteleien.de:80/tetrahedron.htm. Erişim tarihi: 2010-10-19. 
4. "Piero della Francesca's Tetrahedron Formula". http://www.mathpages.com/home/kmath424.htm. Erişim tarihi: 2010-10-19. 
5. "Skew_lines". 29 Mayıs 2015 tarihinde kaynağından arşivlendi. http://web.archive.org/web/20150529074213/https://en.wikipedia.org/wiki/Skew_lines. Erişim tarihi: 2010-10-19. 
6. Klein, Douglas J. (2002). "Resistance-Distance Sum Rules" (PDF). Croatica Chemica Acta 75 (2): 633–649. http://jagor.srce.hr/ccacaa/CCA-PDF/cca2002/v75-n2/CCA_75_2002_633_649_KLEIN.pdf. Erişim tarihi: 2006-09-15. 
7. Vondran, Gary L. (April 1998). "Radial and Pruned Tetrahedral Interpolation Techniques" (PDF). HP Technical Report HPL-98-95: 1–32. http://www.hpl.hp.com/techreports/98/HPL-98-95.pdf. 
8. William Lowthian Green (1875). Vestiges of the Molten Globe, as exhibited in the figure of the earth, volcanic action and physiography. Part I. London: E. Stanford. OCLC 3571917. http://books.google.com/books?id=9DkDAAAAQAAJ. 
9. Arthur Holmes (1965). Principles of physical geology. Nelson. s. 32. http://books.google.com/books?id=XUJRAAAAMAAJ. 
10. Charles Henry Hitchcock (January 1900). Newton Horace Winchell. ed. William Lowthian Green and his Theory of the Evolution of the Earth's Features. XXV. Geological Publishing Company. s. 1–10. http://books.google.com/books?id=_Ty8AAAAIAAJ&pg=PA1. 

Ayrıca bakınız

• Matematiksel şekillerin listesi
• Dörtyüzlüsel sayı
• Tetra Pak