Birim öğe

Matematikte birim öğe veya birim eleman ya da nötr eleman, bir kümenin özel bir öğesidir. Bir kümede herhangi bir öğeyle işleme girdiğinde yine aynı öğeyi verir. Genel olarak e ile gösterilir.

Her a 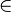$\in$ A için öyle bir e 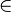$\in$ A vardır ki ea=ae=a olur.

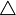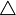A kümesinde tanımlı bir $\triangle$ işlemi için, bu kümedeki her eleman için $x \triangle e=e\triangle x=x$ olacak şekilde bir "e" elemanı varsa "e"ye $\triangle$ işleminin etkisiz elemanı (ya da birim elemanı) denir.

Örneğin, toplama işleminin etkisiz elemanı 0 iken çarpma işlemininki 1 dir. Bu öğenin kümede biricik olduğu rahatlıkla gösterilebilir:

Diyelim bu koşulu sağlayan iki birim öğe var: e ve e' . Eğer bu ikisini işleme sokarsak, e=ee'=e'e=e' olduğu görülür.

Örnekler

küme	işlem	birim
reel sayılar	+ (toplama)	0
real sayılar	· (çarpma)	1
negatif olmayan sayılar	a^b (üslü)	1 (yalnızca sağ birim)
tam sayılar (genişletilmiş rasyonellere
doğal sayılar	ortak kat	1
doğal sayılar	ortak bölen	0
m'ye-n'lik matrisler	+ (matris toplamı)	sıfır matris
n'ye n'lik kare matris	matris çarpımı	In (birim matrisii)
m'ye n'lik matrisler	$\circ$ (Hadamard çarpımı)	Jm, n (Birler matrisi)
bir M kümesindeki tüm fonksiyonlar	∘ (bileşke fonksiyon)	birim fonksiyon
bir G grubundaki tüm dağılımlar	∗ (konvolüsyon)	δ (Dirac delta fonksiyonu)
genişletilmiş reel sayılar	minimum	+∞
genişletilmiş reel sayılar	maksimum	−∞
bir M kümesinin alt kümeleri	∩ (kesişimi)	M
kümeler	∪ (birleşimi)	∅ (boş küme)
koşullar, sıralamalar	birleştirme	boş koşul, boş liste
bir boolean cebri	∧ (mantıksal kesişim)	⊤ (doğru)
bir boolean cebri	∨ (mantıksal birleşim)	⊥ (yanlış)
bir boolean cebri	⊕ (veya değil)	⊥ (yanlış)
düğümler	düğüm toplamı	düğümsüz
kapalı manifold	# (düğüm toplamı)	S^2
yalnızca {e, f}  iki ögesi	∗ şöyle tanımlanır; e ∗ e = f ∗ e = e ve f ∗ f = e ∗ f = f	hem e hem de f sol birimlerdir, fakat sağ birim yoktur iki taraflı birim yoktur