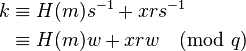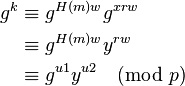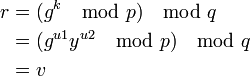Dijital İmza Algoritması
Dijital İmza Algoritması dijital imza için bir FIPS standardıdır. Ağustos 1991’de National Institute of Standards and Technology (NIST) tarafından tasarlanmıştır. Dijital imza algoritması, ElGamal İmza Algoritması'nın bir varyantıdır.
Anahtar Oluşturma
Anahtar oluşturma iki aşamadan oluşur. İlk aşama sistemdeki farklı kullanıcılar arasında paylaşılabilen “algoritma parametreleri”nin seçimiyken ikinci aşama tek bir kullanıcı için açık ve gizli anahtarların hesaplanmasıdır.
Parametre Oluşturma
- Onaylı bir kriptografik özet fonksiyon olan H'yi seç. H olarak SHA-1 kullanılırdı, fakat şu anki DSS’de SHA-1'den daha güçlü olan SHA-2 kullanılmaktadır. Özet fonksiyonun çıktısı anahtar ikilisinin boyutuna kısaltılabilir.
- Anahtar uzunluğu L ve N nin belirlenmesi. Bu, anahtarın kriptografik gücünün belirlenmesinin en önemli ölçütüdür. Orijinal Dijital İmza Standardı L’nin değerini 512 ile 1024’ün arasında 64’ün katı olarak kısıtlamıştır.
- N-bit uzunluğunda asal bir q' değeri seç. Nnin uzunluğu özet fonksiyonun çıktı değerinden kısa ya da eşit olmalıdır.
- p–1, q nun katı olacak şekilde L -bit uzunluğunda asal p modülüsünü seç.
- Çarpımsal mertebesi modulo p de q olan bir g değeri seç. Bu rastgele bir h (1 < h < p−1) değeri için g = h(p–1)/q mod p ile yapılabilir. Eğer sonuç 1 olarak gelirse farklı h değerleri için dene. hnin çoğu değeri g' olarak kullanılabilir; daha çok h=2 kullanılmaktadır.
Algoritma parametreleri olan (p, q, g) sistemdeki farklı kullanıcılar arasında paylaşılabilir.
Kullanıcı anahtarları
Parametre seti verildiğinde, ikinci aşamada tek bir kullanıcı için gizli ve açık anahtarlar üretilir:
- Rassal olarak 0 < x < q olacak şekilde birx seç .
- y = gx mod p değerini hesapla.
- Açık anahtar (p, q, g, y). Özel anahtar x.
h(p–1)/q mod p ve gx mod p, modüler üslerini almak için etkili algoritmalar mevcuttur( Exponentiation by squaring gibi).
İmzalama
H bir özet fonksiyon ve m mesaj olsun :
- 0 < k < q olacak şekilde her bir mesaj için rassal bir k değeri üret.
- r = (gk mod p) mod q değerini hesapla.
- r = 0, ise farklı rassal bir k değeri ile tekrar baştan başla
- s = (k−1(H(m) + x•r)) mod q değerini hesapla
- Eğer s = 0, ise farklı rassal bir k değeri ile tekrar baştan başla.
- İmza (r, s)
İlk iki adım kullanıcı anahtarı oluşturmaya yarar. İmzalama işleminde hesaplaması en pahalı kısım modüler üs alma işlemidir.'k'nın modüler tersinin hesaplanması −1 mod q ikinci en pahalı kısımdır. Genişletilmiş Öklid Algoritması ya da Fermat'nın son teoremi kq−2 mod q kullanılarak hesaplanabilir.
Doğrulama
- Eğer 0 < r < q ya da 0 < s < q sağlanmazsa imzayı reddet.
- w = s−1 mod q değerini hesapla.
- u1 = H(m)•w mod q değerini hesapla.
- u2 = r•w mod q değerini hesapla.
- v = ((gu1•yu2) mod p) mod q değerini hesapla
- Eğer v = r ise imza kabul edilir.
Algoritmanın Doğruluğu
Eğer doğrulayıcı gerçek imzaları her zaman kabul ediyorsa imza şeması doğrudur. Algoritmanın doğruluğu şu şekilde ispatlanabilir:
İlk olarak, eğer g g = h(p − 1)/q mod p ise Fermat'nın son teoremi ile gq ≡ hp − 1 ≡ 1 (mod p) ‘dir. g > 1 ve q asal olduğundan, g’nin mertebesi q’dur.
İmzalayan kişi
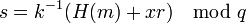 değerini hesaplar.
değerini hesaplar.
Böylece
gnin mertebesi q (mod p) q olduğundan
Sonuç olarak, Dijital İmza Algoritmasının doğruluğu aşağıdaki gibi hesaplanarak çıkar.
Duyarlılık
Dijital İmza Algoritmasında k rassal imza değerinin entropisi, gizliliği ve tek olması önemlidir. Bunlardan birinin olmaması halinde saldıran gizli anahtarı açığa çıkartabilir.Aynı değer iki kez kullanılırsa (kyı gizli tutsa bile), tahmin edilebilir bir değer kullanılarak ya da birkaç imzadaki k nın bazı bitleri sızdırılarak Dijital İmza Algoritması kırılabilir.