Fresnel integrali
.svg.png)
Fresnel integrali, S(x) ve C(x), iki transendental fonksiyon'dur. Augustin-Jean Fresnel'e atfedilmiştir ve optikte kullanılmaktadır. Yakın alan Fresnel difraksiyon fenomeninde ortaya çıkar; aşağıdaki integral gösterimi ile tanımlanırlar:
S(x) ve C(x)'in eş zamanlı parametrik çizimleri, Cornu spirali veya klotoid olarak bilinen Euler spirali'dir.
Tanım
.svg.png)
Fresnel integralinin kuvvet serisi açılımı bütün x 'ler için yakınsaktır:
ifadesi Abramowitz ve Stegun gibi bazı yazarlar (denk. 7.3.1 – 7.3.2) tarafından S(x) ve C(x)'i tanımlayan integrallerin argümenti olarak kullanılır. Bu fonksiyonların eldesi için, yukarıdaki integraller ve x argümenti ile bölünür.
Euler spirali
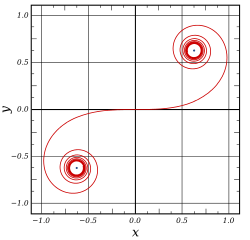
Euler spirali,aynı zamanda Cornu spirali olarak da bilinir. veya clothoid denir,S(t) ye karşı C(t) olarak bir parametrik koordinat tarafından yaratılan grafiktir.Cornu spirali Marie Alfred Cornu tarafından bilim ve mühendislikte bir nomogram olarak kırınım hesabı şeklinde yaratılmış idi. .
Fresnel integralinin tanımı,sonsuzküçük dx ve dy olmak üzere:
Böylece orijinden spiralin uzunluk ölçümü şöyle ifade edilebilir:
Bu , t parametresi orijinden (0,0) ve sonsuz uzunluğu Euler spirali idi . Spiral boyunca bu vektör [cos(t²), sin(t²)] aynı zamanda birim tanjent vektör olarak ifade edilir ,θ = t² olarak alınıyor.eğrinin uzunluğu t dir, eğrilik, olarak ifade edilebilir:
Ve eğriliğin değişim oranı ile birlikte eğrinin uzunluğu:
Euler spiralinin bir özelliği eğriliğidir.Herhangi bir noktanın orijinden ölçümü spiral boyunca mesafeyle orantılıdır. Bu özellik kullanılarak Karayolu ve demiryolu mühendisliğinde geçiş eğrisi kullanılır.
bir araç birim hızda spiral takip ediyorsa yukardaki türev içinde t aynı zamanda zamanı temsil eder.Bu aracın spiralde izleyeceği yol sabit hız sabit bir oranda açısal hız olacak.
Euler spirali bölümünden yapan adına "clothoid döngüsü olarak" roller-coaster döngüsü şeklinde bilinir
Özellikleri
- x ın fonksiyonu C(x) ve S(x) Tek fonksiyon'dur .
- C ve S Tam fonksiyondur.
- Kuvvet serisi açılımı kullanılarak,karmaşık sayı boyutuna genişletilebilir, ve kompleks değişkenlianalitik fonksiyonadını alır.Fresnel integrali hata fonksiyonu'na genişletilebilir:
- C(x) ve S(x) integrallerinin tanımı terimlerin içinde kapalı form temel fonksiyonu terimleri içinde,özel durumlar dışında geliştirilemez. Bu fonksiyonlar limit'ler x sonsuza giderken bilinebilir:
Geliştirme
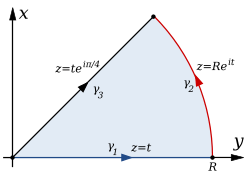
C ve Sin limiti karmaşık analiz metodu ile açısının eğimi sonsuza giderken bulunabilir. Burada kullanılan fonksiyonun kontür integrali:
karmaşık düzlem içindeki sektör-şeklindeki bölge pozitif x-ekseni tarafından , y = x, x ≥ 0,yarı-ekseni ve sınır etrafındaki orijin merkezi R yarıçaplı dairedir .
integral boyunca R sonsuza giderken, dairesel yay eğimi 0'dır, Gauss integrali'nin gerçel-eksen boyunca integral eğimi
ve sonrası rutin dönüşümleri,integral boyunca ilk çeyrek açıortayı Fresnel integralinin limiti ile ilişkili olabilir.
Genelleme
Fresnel integrali aşağıdaki fonksiyon tarafından genelleştirilebilir.
bununla birlikte sol-yanda a>1 için yakınsak ve sağ-yanda tüm düzlemin 'nın yalancı kutuplarının analitik uzantıları daha az olacaktır
Ayrıca bakınız
- Matematiksel fonksiyonların listesi
- Augustin-Jean Fresnel
- Fresnel bölgesi
- Tam geçiş eğrisi
- Euler spirali
- Bölge yüzeyi
Kaynakça
- Eric W. Weisstein, Fresnel Integrals (MathWorld)
- Eric W. Weisstein, Cornu Spiral (MathWorld)
- R. Nave, The Cornu spiral, Hyperphysics (2002) (Uses πt²/2 instead of t².)
- Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972. (See Chapter 7)
- "Roller Coaster Loop Shapes". 23 Eylül 2008 tarihinde kaynağından arşivlendi. http://web.archive.org/web/20080923190052/http://fy.chalmers.se:80/LISEBERG/eng/loop_pe.html. Erişim tarihi: 2008-08-13.