Optik

Optik, ışığın dağılımını da inceler

Optik
Işığın doğası
Işık
Işık hızı
Huygens ilkesi
Fermat ilkesi
Optik aygıtlar
Ayna
Mercek
Prizma
Büyüteç
Kamera
Mikroskop
Teleskop
Lazer
Göz
Olaylar
Yansıma
Toplam iç yansıma
Kırılma
Saçılma
Girişim
Kırınım
Kutuplanma

Optik, ışığın davranışını, özelliklerini, madde ile etkileşimini inceleyen; ışığı kullanan, tespit eden optik aygıt yapımında yararlanılan fiziğin alt dalı.^[1] Optik genellikle görünür, morötesi ve kızılötesi ışığın hareketini inceler. Çünkü ışık bir Elektromanyetik dalgadır ve diğer elektromanyetik dalga türleri(X-ray, mikrodalga, radyo dalgaları gibi) ile benzer özellikler gösterir.^[1]

Çoğu optik olay ışığın klasik elektromanyetizma tanımı ile açıklanabilmektedir. Işığın elektromanyetik tanımlarını tam anlamıyla pratikte kullanmak zordur. Pratik (uygulanabilir) optikte genelde basitleştirilmiş modeller kullanılır. Bu modellerin en yaygını olan geometrik optik; ışığı bir demet olarak ele alır ve ışığı yüzeylerden yansırken, geçerken bükülen bir çizgi varsayar. Fiziksel optik ise ışığın daha kapsamlı bir modelidir. Geometrik optikle açıklanamayan dalga, kırınım, girişim olaylarını barındırır. Tarihsel olarak ışığın demet temelli modeli dalga modelinden önce geliştirilmiştir. 19. yüzyılda elektromanyetik teorideki gelişim ışık dalgalarının aslında elektromanyetik dalga olduğunu göstermiştir.

Bazı optik fenomenleri dalga parçacık ikiliğini ortaya çıkarır. Bu etkiler kuantum mekaniği ile açıklanır. Işığın parçacık modeli söz konusu olduğunda ışık foton adı verilen parçacıkların birleşimi olarak modellenir. Kuantum optiği, kuantum mekaniğini optik sistemlerine uyarlar.

Optik bilimi; astronomi, mühendislik türleri, fotoğrafçılık, tıp (Ağırlıklı olarak Oftalmoloji ve Optometri) gibi alanlarla ilişkilidir ve bu alanlarla ortak çalışır. Optiğin günlük hayatta ve teknolojide uygulaması çok fazladır: ayna, mercek, teleskop, mikroskop, lazer, fiberoptik gibi günlük eşyalarda optik biliminden yararlanılır.

Tarihçe

British Museum'da bulunan Nimrud Merceği (Nemrut Merceği)

Optiğin tarihi Antik Mısır ve Mezopotamya uygarlıklarının merceği geliştirmesiyle başlar. Bilinen ilk mercekler M.Ö. 700'lerde Asurlular tarafından cilalı kristalden, genellikle Kuartz, yapılmıştır. Layard/Nimrud Merceği bunun bir örneğidir.^{[2] [3]} Antik Romalılar, cam kürelere su doldurup mercek olarak kullanmışlardır. Optik alanında gelişmeler ışık teorilerinin ve Yunan, Hint filozoflarının görme teorilerinin gelişmesini beraberinde getirdi. Bu ilerlemeler Greko-Romen kültüründe geometrik optiğin gelişimini sağladı. "Optik" sözcüğü Yunanca görünüş, görünüm anlamına gelen "ὀπτική" sözcüğünden türemiştir.^[3]

Yunan felsefesi görme eyleminin nasıl gerçekleştiği konusunda iki teoriye ayrılmıştır; emisyon (yayılma) ve içe giriş teorisi.^[4] İçe giriş teorisine göre nesnelerden nesnenin kopyaları (eidola) göze gelir ve kopya göz tarafından yakalanınca görme eylemi gerçekleşir. Demokritos, Epikür, Aristoteles ve öğrencilerinin de desteklediği bu teori modern görme teorileriyle ortak yanlara sahip olsa da ortaya atıldığı dönemde hiçbir deneysel çıkarıma dayanmamaktaydı.

Platon, ilk olarak yayılma teorisinde görme olayını; maddelerden yayılan ışınların göz tarafından soğurulması olarak açıklamıştır. Platon aynı zamanda Timaeus'da aynaların dönüşümçarpanına değinmiştir.^[5] Birkaç yüzyıl sonra Öklid Optik tezi yazdı. Bu tezinde görme olayını geometriyle birleştirdi ve "Geometrik Optik"i geliştirdi.^[6] Her ne kadar gözden çıkan ışının her göz kırpmada gözde parlamalara sebep olması gerektiğini sorgulasa da Öklid bu çalışmasını Platon'un perspektifin matematiksel kurallarını ve kırılımın etkilerini nitel olarak açıkladığı yayılım teorisini baz alarak yaptı.^[7] Batlamyus, Optik tezinde içe-dışa yayma teorisini düzenledi: gözden gelen ışınlar (ya da akı) koni şeklini alır, tepesi göze girer ve taban görüş alanını belirtir. Işınlar hassastı, gözlemcinin beynine mesafe ve yüzeyin yönü hakkında bilgi iletiyordu. Aslında Öklid'i özetlemiştir ve ışınla geliş açısı arasındaki ampirik ilişkiyi farkedememiş, kırılma açısını ölçmek için yöntem aramıştır.^[8]

Ibn Sahl'ın el yazısı ile kırılmayı (Şimdiki adıyla Snell yasası) anlatan sayfa

Orta Çağ'da Yunanların optik hakkındaki görüşleri Müslüman dünyası bilim adamları tarafından yeniden gündeme getirilip, geliştirildi. Bu bilim adamlarının öncülerinden olan Kindi, Aristotesyen ve Öklidyen optiğin yararlarını yazmış, optik fenomeni daha iyi açıkladığını düşündüğü için yayılım teorisini benimsemiştir.^[9] 984 yılında İranlı matematikçi Ibn Sahl, "Yanan (Parlayan) aynalar ve mercekler" üzerine bir tez yazdı. Şimdiki adıyla Snell yasası'nı yani ışığın kırılımını açıklamıştır.^[10] Ve bu yasayı merceklerin ve küresel aynaların optimum eğriliğini hesaplamak için kullandı. 11. yüzyılın başlarında, İbn-i Heysem Optik Kitabı'nı (Kitab al-manazir) yazdı. Bu kitapta yansıma ve kırılmayı açıkladı. Aynı kitapta görme olayını ve ışığı açıklamak için gözlem ve deneye dayalı yeni bir sistem önerdi.^{[11][12][13][14][15]} Batlamyus'un ışınların gözden emildiğini söyleyen optik yayılma teorisini reddetti. Bunun yerine ışığın tüm yönlerden, düz çizgiler halinde gözlenen nesnenin her noktasından yansıyıp göze girdiğini öne sürdü. Fakat gözün ışınları nasıl yakaladığını açıklayamadı.^[16] İbn-i Heysem'in çalışması Arap dünyasında görmezden gelinse de 1200 yılında anonim bir yazar tarafından Latince'ye çevrildi. Daha sonra Polonyalı Witelo adlı bir keşiş tarafından özetlendi ve genişletildi. Bu metin 400 yıl boyunca Avrupa'da optik üzerine literatür kitap olarak kullanıldı.^[17]

13. yüzyıl Ortaçağ Avrupasında İngiliz piskopos Robert Grosseteste, ışıkla ilgili bilimsel konuları Aristo'nun ve Platon'un çalışmalarından yola çıkarak geniş bir şekilde, 4 farklı perspektifle ele aldı: epistemolojik, metafiziksel veya kozmogoniksel, etiyolojik veya fiziksel ve teolojik.^[18] Grosseteste'nin en tanınmış öğrencisi, Roger Bacon; İbn-i Heysem, Aristo, İbn-i Sina, İbn Rüşd, Öklid, Kindi, Batlamyus, Tideus, Constantinus Africanus gibi bilim insanlarının yakın zamanda çevrilmiş optik ve felsefe konulu eserlerinden alıntılar ile bir çalışma yaptı. Bacon cam küre parçalarını büyüteç gibi kullanarak ışığın nesnelerden kaynaklanmadığını, nesnelerden yansıdığını ortaya koydu.

İlk takılabilir gözlük 1286 yılı civarında İtalya'da icat edildi.^[19] Bu icat mercekleri bileyerek ve cilalayarak gözlük yapılmasını sağlayan optik endüstrisinin başlangıcıydı. İlk olarak Venedik ve Floransa'da 13. yüzyılda başlamış^[20] daha sonra Hollanda ve Almanya'da da gözlük merceği yapım atölyeleri açılmıştır.^[21] Gözlük yapımcıları görüşü düzeltmek için zamanın optik teorisinden (merceklerin nasıl çalıştığını açıklayamıyordu) edindikleri bilgilerle değil merceklerin etkilerini inceleyerek öğrendikleri bilgilerle farklı mercek tipleri geliştirdiler.^[22][23] Mercek alanındaki gelişmeler, ustalaşma ve deneyler; 1595'de bileşik ışık mikroskobunun, 1608'de refrakter teleskopun Hollanda'daki mercek atölyelerinde icat edilmesini sağladı.^[24][25]

17. yüzyılın başlarında Johannes Kepler geometrik optikte ilerleme kaydetmiştir. Kepler mercekleri, düz ve küresel aynalarda yansımayı, iğne deliği kameranın çalışma prensibini, ışığın yoğunluğunun ters kare yasası ile ilişkisini, Ay ve Güneş tutulmasını, ıraklık açısını açıklamıştır. Aynı zamanda retinanın görüntüleri kaydetme rolü olduğunu anlamış ve mercek yapımcılarının 300 yıllık gözlemlerinin ardından değişik mercek çeşitlerinin etkileri bilimsel olarak ölçülmüştür.^[26] Teleskobun icadından sonra Kepler; teleskobun çalışma prensibinin teorik temellerini oluşturmuş; teleskoplar için Kepler teleskobu olarak bilinen ve büyütmeyi arttırmak için iki dışbükey mercek kullanan daha iyi bir yöntem geliştirmiştir.^[27]

Newton'un kitabı Opticks'in ilk baskısının (1704) kapağı

Optik teori 17. yüzyılın ortalarında René Descartes'ın The World adlı eserinde bulunan tezlerle ilerleme kaydetti. Bu tezlerde yansıma ve kırılma ,ışığın onu üreten nesneler tarafından emildiği varsayılarak, açıklandı.^[28] Bu antik Yunan yayılma teorisinden çok farklıydı. 1660'ların sonlarına doğru, Newton Descartes'in fikrini Işığın Tanecik Kuramı'na dönüştürdü. Bu kurama göre beyaz ışık bir prizma aracılığıyla içeriğindeki renklere ayrılabilen birçok rengin karışımıydı. 1690'da Christiaan Huygens, 1664'te Robert Hooke tarafından yapılan çıkarımlara dayanarak dalga teorisini önerdi. Hooke, Newton'ın ışık teorilerini halka açık bir şekilde eleştirdi. İkisi arasındaki anlaşmazlık Hooke'un ölümüne kadar sürdü. 1704 yılında Newton, Opticks'i yayınladı. Fiziğin diğer alanlarındaki başarısı sebebiyle yaşadığı dönemde ışığın doğası tartışmasının galibi olarak düşünülüyordu.^[28]

Newtonyen optik 19. yüzyılın başlarına kadar kabul gördü ta ki Thomas Young ve Augustin-Jean Fresnel'in girişim deneyleri ile ışığın dalga modelini yayınlamasına kadar. Young'ın meşhur çift yarık deneyi ışığın süperpozisyon ilkesine uyduğunu gösterdi. Bu durum Newton'ın parçacık teorisinde öngörülmemişti. Bu çalışma ışığın kırınım teorisine yönlendirdi ve fiziksel optikte yeni bir çalışma alanı yarattı.^[29] 1860'larda dalga optiği James Clerk Maxwell tarafından elektromanyetik teori ile başarıyla birleştirildi.^[30]

Optik teorideki bir sonraki gelişme 1899 Max Planck'ın siyah cisim ışımasını doğru olarak modellemesi oldu. Bu modelde Planck madde ile ışık arasındaki enerji değişimlerinin sadece kuanta adını verdiği belirli enerji düzeylerinde gerçekleşebildiği varsaydı.^[31][32] 1905'de Albert Einstein kuantizasyonun ışığın kendisinden kaynaklandığını açıklayan fotoelektrik etki teorisini yayınladı.^[33][34] 1913'de Niels Bohr atomların sadece belirli ve kesikli enerji düzeylerinde enerji yayıldığını gösterdi. Bu keşif emisyon ve absorpsiyon spektroskopisindeki kesikli çizgileri açıkladı.^[35] Işık ve madde arasındaki etkileşimin anlaşılması kuantum optiğinin temelini atmasının yanı sıra kuantum mekaniğinin bir bütün olarak geliştirilmesinde önemli bir rol oynadı. Sonuç olarak; kuantum elektrodinamiği tüm optik ve elektromanyetik süreci sanal ve gerçek fotonların değişimi olarak açıkladı.^[36]

Kuantum optiği 1953'de maserin, 1960'da lazerin icadıyla günlük hayatta kullanım bakımından önem kazandı.^[37] Paul Dirac'ın kuantum alan kuramı üzerine çalışması ve George Sudarshan, Roy J. Glauber, Leonard Mandel'in katkıları 1950 ve 1960'larda fotodedektör, istatiksel mekanik alanlarında daha fazla bilgi edinmek için kuantum teorisinin elektromanyetik alana uygulanmasını sağladı.

Klasik optik

Klasik optik iki ana dala ayrılır: geometrik optik ve fiziksel optik. Geometrik optikte, ya da ışın optiği, ışığın düz çizgiler üzerinde yol aldığı varsayılır. Fiziksel optikte, ya da dalga optiği, ışık elektromanyetik bir dalga olarak düşünülür.

Geometrik optik, dalgaboyu optik elemanlar ve modellenen sistem için çok küçükse fiziksel optiğin indirgenmiş hali olarak düşünülebilir.

Geometrik optik

Işık ışınlarının yansıması ve kırılması

Geometrik optik ya da ışın optiği, ışığın dalga olarak yayılmasını farklı ortamlara geçerken yansıma veya kırılma yasalarıyla düz yolda ilerleyen ışınlar şeklinde gösterir.^[38] Bu yasaların ampirik keşfi 984 yıllarına kadar uzanır.^[10] Bu süreç içinde optik cihaz ve araç tasarımında bu yasalar kullanılmıştır. Yasalar şu şekilde özetlenebilir:

Işık ışını iki geçirgen yüzey arasından geçerken yansıyan ve kırılan ışınlar olmak üzere ikiye ayrılır.

Yansıma yasasına göre yansıyan ışın aynı düzlemde kalır ve ışığın yansıma açısı gelme açısına eşittir.

Kırılma yasasına göre kırılan ışın aynı düzlemde kalır ve kırılma açısının sinüsünün gelme açısının sinüsüne oranı sabit bir sayıdır.

${\displaystyle {\frac {\sin {\theta _{1}}}{\sin {\theta _{2}}}}=n}$

n herhangi iki sayı için değişkendir ve ışığın rengini verir. Kırılma indisi olarak bilinir.

Yansıma ve kırılım yasaları Fermat ilkesinden çıkarılabilir. Bu ilkeye göre: bir ışık ışını herhangi iki nokta arasında ilerlerken, izlediği yol en az zamanı gerektiren yoldur.^[39]

Yaklaşımlar

Geometrik optik genellikle paraksiyal yaklaşım ya da "küçük açı yaklaşımı" ile basitleştirilir. Bunun sonucunda matematiksel işlemler doğrusal olur. Böylece optik bileşenler ve sistemler basit matrislerle açıklanabilir. Bu Gaussyan optiğin temelidir ve paraksiyal ışın izleme ile birlikte bir optik sistemin resim ve nesnenin yaklaşık konumu, büyütme gibi temel özelliklerini bulmada kullanılır.^[40]

Yansıma

Yansımalar ikiye ayrılır: düzgün yansıma ve dağınık yansıma. Düzgün yansıma, ışığın ayna gibi parlak yüzeylerden basitçe ve öngörülebilir bir şekilde yansımasıdır. Düzgün yansımada yansıyan görüntünün konumu gerçek olabileceği gibi sanal da olup uzayda tahmin edilebilir bir konumda olabilir. Dağınık yansıma; opak, berrak olmayan, kağıt ve kaya gibi nesnelerin yüzeyinde gerçekleşen yansımadır. Bu yüzeylerdeki yansımalar, yansıyan ışığın ,kaynak yüzeydeki materyalin mikroskobik yapısına bağlı olarak, tam dağlımı ile sadece istatistiksel olarak belirlenebilir. Birçok dağınık yansıtıcının özelliği Lambert Kosinüs Yasası ile açıklanır ya da tahmin edilir. Bu yasa herhangi bir açıdan bakıldığında aynı parlaklığı veren yüzeylerde kullanılır. Parlak yüzeylerde hem dağınık hem de düzgün yansıma görülebilir.

Düzgün yansımada yansıyan ışının yönü, gelen ışının yüzey normali (ışının yüzeye değdiği noktadan çizilen dikme) ile yaptığı açıya göre belirlenir. Gelen ışın, yansıyan ışın ve normal aynı düzlemdedir. Gelen ışının normalle yaptığı açı yansıyan ışının normalle yaptığı açıya eşittir.^[41] Bu aynı zamanda Yansıma Yasası olarak da bilinir.

Düzlem aynalarda yansıma yasasına göre nesnenin görüntüsü, nesnenin aynaya uzaklığına eşit mesafede düz ve aynanın arkasında oluşur. Nesne ile görüntünün boyu eşittir. Yasa aynı zamanda ayna görüntüsünü dönüşümçarpanı ile sağ-sol farkına sebep olduğunu da ifade eder. İki (ya da herhangi bir çift sayı) defa yansımaya uğramış bir nesnenin görüntüsünde dönüşüm (sağ-sol farkı) yoktur. Köşe yansıtıcılar ışının izlediği yoldan geri dönmesini sağlar.^[41]

Yüzeyleri kavisli olan aynalar ışın izleme ile ve yüzeyinin her noktasında yansıma yasası kullanılarak modellenebilir. Parabolik yüzeye sahip aynalarda ise birbirine paralel ışınlar aynadan yansır ve ortak bir odakta birleşirler. Diğer kavisli yüzeyler de ışığı odaklayabilir fakat ışınlar ıraksak şekle sahip aynalarda saparak sonsuzda odaklanır. Özellikle küresel aynalar, küresel sapmaya neden olur. Kavisli aynalar görüntüyü büyütebilir ve küçültebilir ya da büyütme negatif olur. Büyütmenin negatif olması görüntünün ters döndüğünü işaret eder. Düzgün görüntüler sanal, ters görüntüler ise gerçek görüntülerdir. Bu sayede ters görüntüler bir ekrana aktarılabilir.^[41]

Kırınım

Snell Yasası'nı gösteren diyagram. (n₁ < n₂, hava/su gibi)

Kırınım ışık kırılma indisi farklı bir ortama geçerken gerçekleşir. Bu prensip sayesinde mercekler ışığı odaklayabilmektedir. En basit şekilde kırılma; ışık kırılma indisi ${\displaystyle n_{1}}$ olan bir ortamdan kırılma indisi ${\displaystyle n_{2}}$ olan bir ortama geçerken gözlenir. Bu gibi durumlarda Snell yasası ışık ışının sapma miktarını hesaplar:

${\displaystyle n_{1}\sin \theta _{1}=n_{2}\sin \theta _{2}\ }$

burada ${\displaystyle \theta _{1}}$ ve ${\displaystyle \theta _{2}}$ sırasıyla gelen ve kırılan ışının (dalganın) normalle yaptığı açıdır. Bu durum aynı zamanda ortam değişirken ışık hızının da değişimini hesaplamak için de kullanılabilir.

${\displaystyle v_{1}\sin \theta _{2}\ =v_{2}\sin \theta _{1}}$

burada ${\displaystyle v_{1}}$ ve ${\displaystyle v_{2}}$ ilgili ortamdaki dalga hızlarıdır.^[41]

Snell Yasası'nın birçok sonucundan biri de ışık ışınlarının yüksek kırıcılık indisi olan maddeden düşük kırıcılık indisi olan maddeye doğru gitmesidir. Arayüzle temas sonucu tüm ışının yansıyıp hiçbir kısmının emilmemesi de olasıdır. Bu olaya tam yansıma denir ve Fiber optik teknoloji bu mantıkla çalışır. Işık sinyalleri fiber optik kabloda ilerlerken tam yansımaya uğrar bu sayede kablo boyunca ışık kaybı olmaz. Aynı zamanda yansıma ve kırılma kullanarak polarize ışık ışınları elde etmek mümkündür. Kırılan ve yansıyan ışın dik açıyla gelirse yansıyan ışın "düzlemsel (lineer) polarizasyon" özelliği kazanır. Bu gibi durumların gerçekleşmesi için gereken gelme açısına Brewster açısı denir.^[41]

Snell Yasası, ortam doğru ışık ışınlarının kırılma indisi ve geometrisi bilinen "lineer ortam"da sapma miktarlarını ölçmek için kullanılabilir. Örneğin ışığın bir prizmadan geçmesi sonucu ışınların sapması ve yayılması prizmanın şekline ve konumuna bağlıdır. Ek olarak çoğu maddede farklı frekanstaki ışıkların farklı kırılma indisi olduğu için kırılma gök kuşağındaki gibi ışık tayfı üretebilir. Bu olayın keşfi Isaac Newton'a mal edilir.^[41]

Işığı kırabilen maddelerde kırınım indisi pozisyonla aşamalı olarak değişir ve böylece ışık ışınları düz çizgiler halinde değil bükülmüş olarak yol alır. Bu etki; sıcak havalarda havanın kırılma indisinin değişerek ışık ışınlarının bükülmesine ve uzaktaki nesnelerin çeşitli şekillerde (havuz yüzeyinde olduğu gibi) algılanmasına sebep olur. Serap olayı buradan kaynaklanır. Birden fazla kırılma indisine sahip maddelere değişken-indisli (GRIN) maddeler denir. Bu maddeler modern optikte fotokopi makinesi ve tarayıcı gibi cihazların yapımında olduğu gibi birçok alanda kullanılmaktadır. Bu olay Değişken indis optiği alanında incelenir.^[42]

İnce kenarlı mercekte görüntü ve nesne

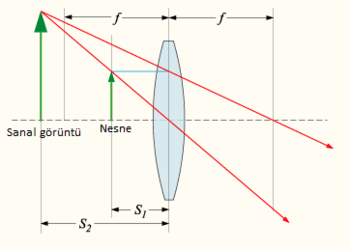
Kırılma ile ışınları birleştiren ya da ayıran cihazlara mercek (lens) adı verilir. İnce mercekler, merceğin iki tarafında da odak noktası oluşturabilirler. Bu noktalar Lensmaker denklemi ile modellenebilir.^[43] Genel olarak iki tip mercek vardır: paralel ışınları birleştiren konveks (dışbükey, ince kenarlı ya da yakınsak) mercek ve paralel ışınları ayıran konkav (içbükey, kalın kenarlı ya da ıraksak) mercek. Merceklerin oluşturduğu görüntünün ayrıntılı tahmini için küresel aynalarda kullanılan ışın izleme yöntemi kullanılabilir. Küresel aynalarda olduğu gibi ince merceklerde de verilen odak noktasının uzunluğu (${\displaystyle f}$) ve nesne uzaklığı (${\displaystyle S_{1}}$) kullanılarak basit bir denklem ile cismin görüntüsünün nerede olduğu belirlenebilir:

${\displaystyle {\frac {1}{S_{1}}}+{\frac {1}{S_{2}}}={\frac {1}{f}}}$

Bu denklemde ${\displaystyle S_{2}}$ görüntünün mesafesini ifade eder ve görüntü ile nesne aynı tarafta ise negatif; farklı tarafta ise pozitif kabul edilir.^[43] Odak uzaklığı ${\displaystyle f}$ konkav merceklerde negatif alınır.

İnce kenarlı mercek şemasal gösterimi

Paralel gelen ışınlar ince kenarlı (konveks) mercek tarafından, merceğin uzak tarafında odaklandırılarak bir odak uzaklığı mesafede ters bir şekilde gerçek görüntüye dönüştürülürler. Sonlu bir mesafedeki nesneden gelen ışınlar odak noktasından daha öte bir noktada odaklanırlar; nesne merceğe yaklaştıkça görüntü mercekten uzaklaşır. Kalın kenarlı (konkav merceklerde), paralel gelen ışınlar mercekten geçtikten sonra mercekten bir odak uzunluğu mesafede, paralel ışınların geldiği mercek tarafındaki düz bir sanal görüntüden kaynaklanmışçasına dağılırlar. Sonlu mesafedeki bir nesneden gelen ışınlar, merceğe odak noktasından daha yakın, nesne ile aynı tarafta olan bir sanal görüntü ile ilişkilendirilirler. Nesne merceğe yaklaştıkça, sanal görüntü de merceğe yaklaşır.

Aynı şekilde, bir merceğin büyütmesi ise aşağıda gösterildiği şekildedir:

${\displaystyle M=-{\frac {S_{2}}{S_{1}}}={\frac {f}{f-S_{1}}}}$

Bu formüldeki eksi (-), bir kongrede alınan karara göre, pozitif ise düz, negatif ise ters nesneleri belirtir. Aynalara benzer olarak, tek mercek ile oluşmuş görüntüler düz ise sanal, ters ise gerçek görüntülerdir.^[41]

Merceklerde odağı ve görüntüyü bozan optik aberasyonlar gözlemlenebilmektedir. Bu aberasyonlar (sapınçlar) geometrik kusurlardan ya da ışığın değişik dalga boyları nedeniyle ortaya çıkan kırınım indeksi değişiminden (kromatik aberasyon) kaynaklanabilmektedir.^[41]

Kaynakça

1. McGraw-Hill Encyclopedia of Science and Technology (5. bas.). McGraw-Hill. 1993. 
2. "World's oldest telescope?". BBC News. 1 Temmuz 1999. http://news.bbc.co.uk/1/hi/sci/tech/380186.stm. Erişim tarihi: 17 Temmuz 2014.  (İngilizce)
3. T. F. Hoad (1996). The Concise Oxford Dictionary of English Etymology. ISBN 0-19-283098-8. 
4. "A History of The Eye". stanford.edu. 1 Eylül 2013 tarihinde kaynağından arşivlendi. http://web.archive.org/web/20130901163402/http://www.stanford.edu/class/history13/earlysciencelab/body/eyespages/eye.html. Erişim tarihi: 17 Temmuz 2014. (İngilizce)
5. T. L. Heath (2003). A manual of greek mathematics. Courier Dover Publications. s. 181–182. ISBN 0-486-43231-9. 
6. William R. Uttal (1983). Visual Form Detection in 3-Dimensional Space. Psychology Press. s. 25–. ISBN 978-0-89859-289-4. http://books.google.com/books?id=rhVOVKp0-5wC&pg=PA25. (İngilizce)
7. Öklid (1999). Elaheh Kheirandish. ed. Öklid'in "Optik" kitabının Arapça kopyası= Kitāb Uqlīdis fī ikhtilāf al-manāẓir. New York: Springer. ISBN 0-387-98523-9. 
8. Batlamyus (1996). A. Mark Smith. ed. Ptolemy's theory of visual perception: Batlamyus'un Optik kitabının eklemelerle İngilizce çevirisi. DIANE Publishing. ISBN 0-87169-862-5. 
9. Adamson, Peter (2006). "Al-Kindi¯ and the reception of Greek philosophy". In Adamson, Peter; Taylor, R.. The Cambridge companion to Arabic philosophy. Cambridge University Press. p. 45. ISBN 978-0-521-52069-0.
10. Rashed, Roshdi (1990). "A pioneer in anaclastics: Ibn Sahl on burning mirrors and lenses". Isis 81 (3): 464–491. DOI:10.1086/355456. JSTOR 233423. 
11. A. I. Sabra and J. P. Hogendijk (2003). The Enterprise of Science in Islam: New Perspectives. MIT Press. s. 85–118. ISBN 0-262-19482-1. OCLC 50252039 237875424 50252039. 
12. G. Hatfield (1996). "Was the Scientific Revolution Really a Revolution in Science?". F. J. Ragep, P. Sally, S. J. Livesey. Tradition, Transmission, Transformation: Proceedings of Two Conferences on Pre-modern Science held at the University of Oklahoma. Brill Publishers. s. 500. ISBN 9004101195. http://books.google.com/books?id=Kl1COWj9ubAC&pg=PA489. 
13. Nader El-Bizri (2005). "A Philosophical Perspective on Alhazen's Optics". Arabic Sciences and Philosophy 15: 189–218. DOI:10.1017/S0957423905000172. 
14. Nader El-Bizri (2007). "In Defence of the Sovereignty of Philosophy: al-Baghdadi's Critique of Ibn al-Haytham's Geometrisation of Place". Arabic Sciences and Philosophy 17: 57–80. DOI:10.1017/S0957423907000367. 
15. G. Simon (2006). "The Gaze in Ibn al-Haytham". The Medieval History Journal 9: 89. DOI:10.1177/097194580500900105. 
16. Ian P. Howard; Brian J. Rogers (1995). Binocular Vision and Stereopsis. Oxford University Press. s. 7. ISBN 978-0-19-508476-4. http://books.google.com/books?id=I8vqITdETe0C&pg=PA7. 
17. Elena Agazzi; Enrico Giannetto; Franco Giudice (2010). Representing Light Across Arts and Sciences: Theories and Practices. V&R unipress GmbH. s. 42. ISBN 978-3-89971-735-8. http://books.google.com/books?id=ipyT7askd8EC&pg=PA42. 
18. Lindberg, D. C. (1976). Theories of Vision from al-Kindi to Kepler. Chicago: Univ. of Chicago Pr.. s. 94–99. 
19. Vincent, Ilardi (2007). Renaissance Vision from Spectacles to Telescopes. Philadelphia, PA: American Philosophical Society. s. 4–5. ISBN 9780871692597. 
20. Helden, Al Van. "The Telescope". The Galileo Project. Galileo.rice.edu. 2 Haziran 2016 tarihinde kaynağından arşivlendi. http://web.archive.org/web/20160602002803/http://galileo.rice.edu/sci/instruments/telescope.html. Erişim tarihi: 22 Temmuz 2014. 
21. Henry C. King (2003). The History of the Telescope. Courier Dover Publications. s. 27. ISBN 978-0-486-43265-6. http://books.google.com/books?id=KAWwzHlDVksC&pg=PR1. 
22. Paul S. Agutter; Denys N. Wheatley (2008). Thinking about Life: The History and Philosophy of Biology and Other Sciences. Springer. s. 17. ISBN 978-1-4020-8865-0. http://books.google.com/books?id=Gm4bqeBMR8cC&pg=PA17. 
23. Vincent Ilardi (2007). Renaissance Vision from Spectacles to Telescopes. American Philosophical Society. s. 210. ISBN 978-0-87169-259-7. http://books.google.com/books?id=peIL7hVQUmwC&pg=PA210. 
24. "Time Line". Nobel Foundation. 9 Ocak 2010 tarihinde kaynağından arşivlendi. http://web.archive.org/web/20100109122901/http://nobelprize.org:80/educational_games/physics/microscopes/timeline/index.html. Erişim tarihi: 22 Temmuz 2014. 
25. Fred Watson (2007). Stargazer: The Life and Times of the Telescope. Allen & Unwin. s. 55. ISBN 978-1-74175-383-7. http://books.google.com/books?id=2LZZginzib4C&pg=PA55. 
26. Vincent Ilardi (2007). Renaissance Vision from Spectacles to Telescopes. American Philosophical Society. s. 244. ISBN 978-0-87169-259-7. http://books.google.com/books?id=peIL7hVQUmwC&pg=PA244. 
27. Casper, Max (1993). Kepler. Courier Dover Publications. s. 198-202. ISBN 0486676056. http://books.google.com/books?id=0r68pggBSbgC&pg=PA198. 
28. A. I. Sabra (1981). Theories of light, from Descartes to Newton. CUP Archive. ISBN 0-521-28436-8. 
29. W. F. Magie (1935). A Source Book in Physics. Harvard University Press. s. 309. 
30. J. C. Maxwell (1865). "A Dynamical Theory of the Electromagnetic Field". Philosophical Transactions of the Royal Society of London 155: 459. Bibcode 1865RSPT..155..459C. DOI:10.1098/rstl.1865.0008. 
31. Planck'ın kuantumun karmaşıklığına entelektüel yaklaşımı katıdır çünkü Planck kuantum etkilerini tam anlamıyla kabul etmemiştir.
32. Kragh, H. (1 Aralık 2000). "Max Planck: the reluctant revolutionary". Physics World. 30 Mayıs 2015 tarihinde kaynağından arşivlendi. http://web.archive.org/web/20150530041012/http://physicsworld.com:80/cws/article/print/2000/dec/01/max-planck-the-reluctant-revolutionary. Erişim tarihi: 23 Temmuz 2014. 
33. Einstein, A. (1967). "On a heuristic viewpoint concerning the production and transformation of light". Ter Haar, D.. The Old Quantum Theory. Pergamon. s. 91–107. http://wien.cs.jhu.edu/AnnusMirabilis/AeReserveArticles/eins_lq.pdf. Erişim tarihi: March 18, 2010. 
34. Einstein, A. (1905). "Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt [On a heuristic viewpoint concerning the production and transformation of light]" (German). Annalen der Physik 322 (6): 132–148. Bibcode 1905AnP...322..132E. DOI:10.1002/andp.19053220607. 
35. "On the Constitution of Atoms and Molecules". Philosophical Magazine 26, Series 6: 1–25. 1913. http://web.archive.org/web/20070704225134/http://dbhs.wvusd.k12.ca.us/webdocs/Chem-History/Bohr/Bohr-1913a.html.  Bohr atom modeli ve Kovalent bağın açıklandığı makale
36. R. Feynman (1985). "Chapter 1". QED: The Strange Theory of Light and Matter. Princeton University Press. s. 6. ISBN 0-691-08388-6. 
37. N. Taylor (2000). LASER: The inventor, the Nobel laureate, and the thirty-year patent war. New York: Simon & Schuster. ISBN 0-684-83515-0. 
38. Ariel Lipson; Stephen G. Lipson; Henry Lipson (28 October 2010). Optical Physics. Cambridge University Press. s. 48. ISBN 978-0-521-49345-1. http://books.google.com/books?id=aow3o0dhyjYC&pg=PA48. Erişim tarihi: 12 July 2012. 
39. Sir Arthur Schuster (1904). An Introduction to the Theory of Optics. E. Arnold. s. 41. http://books.google.com/books?id=X0AcBd-bcCwC&pg=PA41. 
40. J. E. Greivenkamp (2004). Field Guide to Geometrical Optics. SPIE Field Guides vol. FG01. SPIE. s. 19–20. ISBN 0-8194-5294-7. 
41. H. D. Young (1992). "35". University Physics 8e. Addison-Wesley. ISBN 0-201-52981-5. 
42. Marchand, E.W. (1978). Gradient Index Optics. New York: Academic Press. 
43. E. Hecht (1987). Optics (2. bas.). Addison Wesley. ISBN 0-201-11609-X.  Bölüm 5 & 6.