Kepler üçgeni

Alanları, aralarında altın oran bulunacak şekilde, geometrik dizi oluşturan üç karenin oluşturduğu bir Kepler üçgeni.

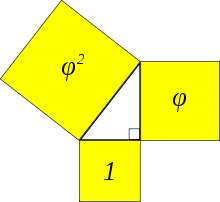
Kepler üçgeni, kenarları geometrik dizi oluşturan bir dik üçgen. Kepler üçgeninin kenarları altın oranla

${\displaystyle \varphi ={1+{\sqrt {5}} \over 2}}$

ilişkilidir; kenar uzunlukları ${\displaystyle 1:{\sqrt {\varphi }}:\varphi }$ ya da yaklaşık olarak 1 : 1,272 : 1,618 ile orantılıdır.^[1] Kenar uzunluklarının kareleri (şekilde gösterildiği gibi), aralarında altın oran bulunacak şekilde, geometrik dizi oluşturur.

Bu orana sahip üçgenler adını, üçgenin kısa kenarıyla hipotenüsü arasında altın oran olduğunu tespit ederek, özelliklerini tanımlayan ilk isim olan Alman matematikçi Johannes Kepler'den almıştır.^[2] İki matematiksel yapıyı, Pisagor teoremi ile altın oran, birleştiren Kepler üçgeni Johannes Kepler'i çok etkilemiştir; Alman matematikçi durumu

Geometride iki büyük hazine vardır: biri Pisagor teoremi, diğeri bir doğrunun sıra dışı ve ortalama (altın) oranla bölünmesi. İlkine bir külçe altın dersek, ikincisine eşsiz, kıymetli, mücevher diyebiliriz.^[3]

—  Johannes Kepler

Bazı kaynaklara göre, Keops Piramidi'nde ölçüleri Kepler üçgenine çok yakın bir üçgen vardır.^[4][5]

Bir Kepler üçgeninin çizimi

Bir altın dikdörtgen kullanılarak Kepler üçgeni çizme yöntemi

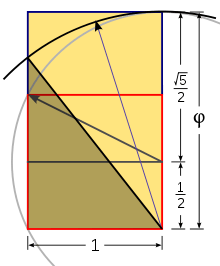
Kepler üçgeni ancak pergel ve cetvel kullanılarak, altın dikdörtgen yardımıyla çizilebilir:

1. Basit bir kare çizilir
2. Karenin bir kenarının orta noktası karşı köşelerden biriyle birleştirilir
3. Oluşan doğru yarıçap kabul edilerek çizilecek çember yayıyla dikdörtgenin yüksekliği oluşturulur
4. Altın dikdörtgen çizimi tamamlanır
5. Altın dikdörtgenin uzun kenarı yarıçap olacak ve dikdörtgenin diğer kenarı kesilecek şekilde bir çember yayı daha çizilerek Kepler üçgeninin hipotenüsü elde edilir

Ayrıca bakınız

• Altın üçgen
• Özel dik üçgenler

Kaynakça

1. Roger Herz-Fischler (2000). The Shape of the Great Pyramid. Wilfrid Laurier University Press. ISBN 0889203245. http://books.google.com/books?id=066T3YLuhA0C&pg=PA81&dq=kepler-triangle+geometric&ei=ux77Ro6sGKjA7gLzrdjlDQ&sig=bngzcQrK9nHOkfZTo5O0ieNdtUs. 
2. Livio, Mario (2002). The Golden Ratio: The Story of Phi, The World's Most Astonishing Number. New York: Broadway Books. s. 149. ISBN 0-7679-0815-5. 
3. Karl Fink, Wooster Woodruff Beman ve David Eugene Smith (1903). A Brief History of Mathematics: An Authorized Translation of Dr. Karl Fink's Geschichte der Elementar-Mathematik (2nd ed. bas.). Chicago: Open Court Publishing Co. http://books.google.com/books?id=3hkPAAAAIAAJ&pg=PA223&dq=%22Geometry+has+two+great+treasures%22&lr=&as_brr=1&ei=sQ1GSI_KH4fstgO_rvCpDQ. 
4. The Best of Astraea: 17 Articles on Science, History and Philosophy. Astrea Web Radio. 2006. ISBN 1425970400. http://books.google.com/books?id=LDTPvbXLxgQC&pg=PA93&dq=kepler-triangle&ei=vCH7RuG7O4H87gLJ56XlDQ&sig=6n43Hhu5pE3TN5BW18tbQJGRHTQ. 
5. Squaring the circle, Paul Calter