Sarmal

Sağ ve sol-elli sarmallar

Sarmal yapılı bir molekülün kristal yapısı (Jean-Marie Lehn ve arkadaşları, Helv. Chim. Acta., 2003, 86, 1598-1624).

Sol-elli sarmal olarak büyüyen bir sarmaşık.

Cedar Point (Ohio, ABD) lunaparkındaki "Corkscrew" eğlence treninin rayı konik sarmal olarak sonlanmaktadır.

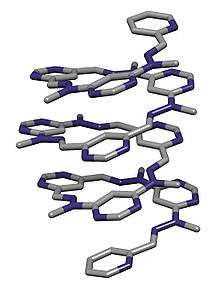
Sarmal (helis, heliks veya helezon), burgu şekilli, üç boyutlu bir şekildir. Sarmal şekilli gündelik nesnelere örnek olarak silindirik yay, vida, ve minare merdiveni gösterilebilir.^[1][2] Sarmallar biyolojide de yer alır, DNA molekülü birbirine sarılmış iki sarmaldan oluşur, çoğu proteinde de alfa sarmal olarak adlandırılan sarmal yapılar bulunur. Sıfat hali için sarmalsal (helisel, helikal, veya helezonî) kullanılır.

Tipleri

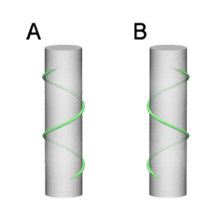
Sarmallar dönüş yönlerine göre sağ elli veya sol elli olarak nitelendirilirler. Sağ elli bir sarmal şöyle tanımlanabilir: hayalinizde sarmalı sağ elinizle tutun, baş parmağınız sarmalın eksenine paralel yönde olsun, diğer parmaklarınızı da sarmalın oyuklarının içine yerleşsin. Eğer parmaklarınızın uçları başparmağınıza doğru yönlenmişse sarmal sağ ellidir. Yoksa, sol elli.

Bir diğer tanıma göre, sarmalın ekseni boyunca baktığınızda sarmalın saat yönünde dönmesi, sarmalın sizden uzaklaşıyor gibi görünmesine neden oluyorsa sarmal sağ ellidir, yoksa sol elli.

Ellilik (veya kirallik) sarmalın bir özelliğidir, bakış açısına göre değişmez: sağ-elli bir sarmal döndürülerek veya çevrilerek sol-elli olamaz, ancak aynadan yansıması ile sol elli görülür (keza, sol-elli sarmal da sağ-elli olamaz).

Çoğu vida sağ-elli sarmal şekillidir. Biyolojideki alfa sarmal, DNA'nın A ve B halleri de sağ-elli sarmallardır. DNA'nın Z hali sol-ellidir.

Bir çift sarmal, geometrik anlamda, aynı eksene sahip iki eşleşik sarmaldır, bunlardan biri ötekinin eksen boyunca ötelenmiş halidir.^[3]

Konik sarmal, bir konik yüzey üzerindeki sarmaldır, koninin tepesine olan uzaklık eksene göre olan açının üssel bir fonksiyonudur.

Dairesel bir sarmalın sabit eğriliği ve torsiyonu olur. Sarmalın hatvesi, sarmal ekseni boyunca ölçülen, sarmalın bir tam dönüşünün genişliğidir.

Bir eğrinin teğetinin bir doğruyla yaptığı açı sabitse, bu eğriye genel sarmal denir.

Matematik

Matematikte sarmal, 3 boyutlu uzayda bir eğri tipidir. Kartezyen koordinat sisteminde aşağıdaki üç denklem bir sarmalı tanımlar^[4]:

${\displaystyle x=\cos(t),\,}$

${\displaystyle y=\sin(t),\,}$

${\displaystyle z=t.\,}$

Sağ-elli bir koordinat sisteminde, t paramatresi artarken, (x,y,z) noktası sağ-elli bir sarmal çizer, bunun çapı 1, z-ekseni boyunca hatvesi 2π'dir.

Silindirik koordinat sisteminde (r, θ, h), aynı sarmal şöyle tanımlanır:

${\displaystyle r=1,\,}$

${\displaystyle \theta =t,\,}$

${\displaystyle h=t.\,}$

Çapı a, hatvesi 2πb olan bir sarmal bu denklemlerle tanımlanır:

${\displaystyle x=a\cos(t),\,}$

${\displaystyle y=a\sin(t),\,}$

${\displaystyle z=bt.\,}$

Bir sarmalı matematiksel olarak oluşturmanın bir diğer yolu, sanal argümanlar kullanan kompleks değerli üssel bir fonksiyonun (e^xi) grafiğini çizmektir (bkz. Euler formülü)

Döndürme, öteleme ve ölçeklemeler dışında, tüm sağ-elli sarmallar yukarda tanımlanan sarmala eşdeğerdir. Eşdeğer sol-elli sarmal birkaç yoldan oluşturulabilir, en kolayı x, y veya z bileşenlerinden birinin negatifini almaktır.

Kartezyen koordinatlarla

${\displaystyle t\mapsto (a\cos t,a\sin t,bt),t\in [0,T]}$a

olarak ifade edilen, a çaplı ve 2πb havleli bir dairesel sarmalın uzunluğu ${\displaystyle T\cdot {\sqrt {a^{2}+b^{2}}}}$, eğriliği ${\displaystyle {\frac {|a|}{a^{2}+b^{2}}}}$ ve torsiyonu ${\displaystyle {\frac {b}{a^{2}+b^{2}}}'dir.}$

Kaynaklar

1. "Helices" by Sándor Kabai, The Wolfram Demonstrations Project.
2. "Helical Staircase" by Sándor Kabai, The Wolfram Demonstrations Project.
3. "Double Helix" by Sándor Kabai, The Wolfram Demonstrations Project.
4. Eric W. Weisstein, Helix (MathWorld)