Zipf yasası

Zipf yasası

Olasılık kütle fonksiyonu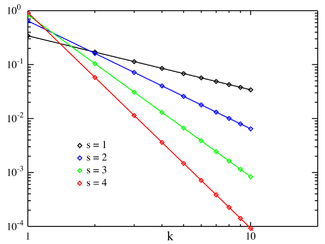 ;;N=10 için Zipf OKF log–log ıskalası üzerindedir. Yatay eksen k endeksidir. (Fonksiyonun k nin sadece tamsayı değerleri ile tanımlandığına dikkat etmek gerekmektedir. Grafikteki noktaların birbirlerine doğrular parçaları ile bağlanmaları devamlılık ifade etmemelidir.) )
Yığmalı dağılım fonksiyonu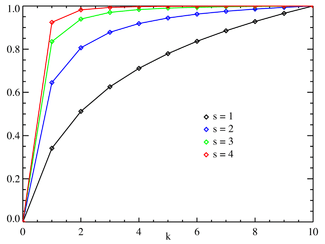 Fonksiyonun k nin sadece tamsayı değerleri ile tanımlandığına dikkat etmek gerekmektedir. Grafikteki noktaların birbirlerine doğrular parçaları ile bağlanmaları devamlılık ifade etmemelidir. )
Parametreler	${\displaystyle s>0\,}$ (reel) ${\displaystyle N\in \{1,2,3\ldots \}}$ (tamsayı)
Destek	${\displaystyle k\in \{1,2,\ldots ,N\}}$
Olasılık kütle fonksiyonu (OYF)	${\displaystyle {\frac {1/k^{s}}{H_{N,s}}}}$
Yığmalı dağılım fonksiyonu (YDF)	${\displaystyle {\frac {H_{k,s}}{H_{N,s}}}}$
Ortalama	${\displaystyle {\frac {H_{N,s-1}}{H_{N,s}}}}$
Medyan
Mod	${\displaystyle 1\,}$
Varyans
Çarpıklık
Fazladan basıklık
Entropi	${\displaystyle {\frac {s}{H_{N,s}}}\sum _{k=1}^{N}{\frac {\ln(k)}{k^{s}}}+\ln(H_{N,s})}$
Moment üreten fonksiyon (mf)	${\displaystyle {\frac {1}{H_{N,s}}}\sum _{n=1}^{N}{\frac {e^{nt}}{n^{s}}}}$
Karakteristik fonksiyon	${\displaystyle {\frac {1}{H_{N,s}}}\sum _{n=1}^{N}{\frac {e^{int}}{n^{s}}}}$

Zipf yasası matematiksel istatistik bilimi kullanılarak ortaya çıkartılan bir empirik yasa olarak formüle edilmiştir. Yasaya ad olarak, 1930'da Amerika'da Harvard Üniversitesi'nde dilbilim profesörü olan George Kingsley Zipf tarafından yayımlanması üzerine, onun adı verilmiştir.^[1][2] Bu empirik yasa herhangi bir insan dili ile yazılmış bir metinde bulunan sözcüklerin sıklılıkları hakkındadır.

Bu yasa daha önce de Alman Felix Auerbach tarafından 1913'de yayımlanmıştır. Ama bu yayımda yapılan sıralama dünya șehirlerinin nüfus itibarıyla sıralanması idi.^[3] Fransız stenografi uzmanı Jean-Baptiste Estoup (1868-1950) de metinlerde bulunan sözcüklerinin sistemik sıklıkları hakkında Zipf'den önce yayım yapmıştır.^[4] Bu sıralamalar şirket büyüklükleri sıralamaları, gelir sıralamaları vb. için de uygulanmıştır. Benoît Mandelbrot bu yasayı genelleştirmiştir.

Zipf yasasının niçin insan dillerinin çoğunda uygulanabileceği bilinmemektedir.^[5]

Basit tanımlama ve örnekler

Dilbilimde bu yasaya göre herhangi bir yazılı metinde geçen sözcükler azalan sıklığa göre (yani en çok kullanılandan en az kullanılana doğru) sıralanırsa, elde edilen sıralama listesindeki tek bir sözcüğün sıra numarası ile o sözcüğün sıklık sayısı her zaman sabit bir sayı olur. Bu daha kolayca, sıra numarası N olan bir sözcük için sıklığın 1/N olması şeklinde ifade edilebilir. Böylece en fazla sıklıkla kullanılan sözcük ikinci sırada sıklıkla kullanılan sözcükten 2 misli daha fazla, üçüncü sıradaki sözcükten 3 misli daha fazla kullanılır.

Bir diğer örnek olarak 10 sözcükten oluşan bir metin dili ele alındığı kabul edilsin ve bu metin dilinde hazırlanan tüm metinlerde en fazla sayda kullanılan sözcüğün 100 defa kullanıldığı kabul edilsin; bu halde yapılan en sık kullanılandan az sık kullanılan sözcüğe göre yapılan sözcük sıralaması (Zipf yasası'na göre) şöyle olacaktır:
1. sözcük => 100/1 = 100
2. sözcük => 100/2 = 50
3. sözcük => 100/3 = 33,3
4. sözcük => 100/4 = 25
5. sözcük => 100/5 = 20
6. sözcük => 100/6 = 16,6
7. sözcük => 100/7 = 14,3
8. sözcük => 100/8 = 12,5
9. sözcük => 100/9 = 11,1
10. sözcük => 100/10= 10

Bu örnekte görüldüğü gibi sıralamadaki ilk sözcüklerin sıklığı diğerlerine göre çok daha fazla olarak gözlenmekte, diğer tüm sözcükler gittikçe azalan sayılarda gözlenmektedir.

İrlanda'lı yazar James Joyce'un "Ulyses" adlı İngilizce romanının ana metinindeki sözcüklerin sıklılıklarının sıralanması.

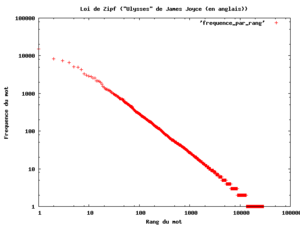
George Kingsley Zipf, İrlandalı yazar James Joyce'un 2 Şubat 1922'de yayınlanan Ulysses adlı romanını ayrıntılı incelemiş ve bu romanda bulunan sözcüklerin sıklığını ve bu sıklığın sıralanmasını bulmuştur. Bu araştırmaya göre

• en fazla sıklıkla kullanılan sözcük 8.000 defa kullanılmış;
• sıklık sıralamasında 10. olan sözcük 800 defa kullanılmış;
• sıklık sıralamasında 100. olan sözcük 80 defa kullanılmış;
• sıklık sıralamasında 1000. olan sözcük 8 defa kullanılmıştır.

Günümüzde bilgisayarlar kullanılarak eldeki en büyük yazılı metinlerde bile sözcük sıralama araştırması birkaç saniyeyi aşmamaktadır ve bunlardan genelleme yapılırsa herhangi bir yazılı metinde gözlenmektedir ki sırası N olan bir sözcük için sıralama fonksiyonu f(N) şu Zipf yasasına uymaktadır:
${\displaystyle f(n)={\frac {K}{n}}}$ burada K bir sabittir.

Zipf yasasının uygulanması en kolay bir şekilde sıralama sıklıklar verisinin bir log-log eksenli grafikte gösterilmesi ve bu verilere doğrusal regresyon tatbiki olmaktadır. Herhangi değişken bir sıralama verisi için; R=sıralama sayıları; N: sıralama sıklığı ve a ve b doğrusal regresyon katsayıları olup
log R = a - b log N
Regresyon doğrusu uygulanırsa ve eğer b=1 bulunursa, verilerin Zipf yasasına uygunluğu kabul edilmesi gerekir.

2004'te yapılan ve dünya şehrilerinin nüfusları sıralamasına uygulanan bir araştırmada genel olarak b = 1.07 bulunmuştur.^[6] Tüm dağılımın log-normal dağılımın uygunluğu ve üst kuyruk verilerinin ise Zipf yasasına uyduğu görülmüştür. Bu çalışmaya göre "the" sözcüğü için
x = log(1) ve y = log(69971).

Teorik gelişme

Bu yasaya göre fiziksel bilimler ve sosyal bilimlerde incelenen verilerin çoğunluğu ayrık üstel yasa olasılık dağılımına ilişkili olan bir Zipf dağılımı yaklaşık olarak ifade edilir. Formel olarak; şu ifadeleri kullanalım:

• N elemanlar sayısı;
• k elemanların sıralaması;
• s dağılımı karakterize eden üssel değer

Zipf yasası N sayıda elemanı bulunan bir ana kitle için, k sıralama numarası gösteren elemanların dağılımını f(k;s,N) fonksiyonu şöyle ifade eder:

${\displaystyle f(k;s,N)={\frac {1/k^{s}}{\sum _{n=1}^{N}(1/n^{s})}}.}$

Eğer her elemanın ortaya çıkma sıklığı da sayıları birbirinden bağımsız ve bir üstel yasa dağılımı, yani
${\displaystyle p(f){=}\alpha f^{-1-1/s}.}$
, gösteren birbiryle tüm olarak aynı olan dağılım gösteren rassal değişkenler ise Zipf yasası geçerlidir.^[7]

İngilizce dilinde bulunan sözcükler örneğine göre N İngilizce dilinde bulunan sözcük sayısı olursa ve klasik Zipf yasası kullanılırsa s in üssel değeri 1 olur. O zaman f(k; s,N) en çok kullanılan sözcüğün kullanılma oranını ifade eder.

Zipf yasası şu şekilde de ifade edilebilir:

${\displaystyle f(k;s,N)={\frac {1}{k^{s}H_{N,s}}}}$

burada H_N,s Ninci genelleştirilmiş harmonik sayı olur.

İstatistiksel açıklama

Wentian Li bu yasanın rassal olarak yaratılmış olan metinlerin istatistiksel analizi ile de kısmen açıklanabileceğini iddia etmektedir. Bir ayrık tekdüze dağılım gösteren alfabede bulunan her harfi (ve boşluk ifade eden karakteri) kapsayan bir kütleden rassal olarak seçilen her bir karakteri ihtiva eden bir metinde bulunan sözcüklerin (yaklaşık olarak log-log eksenli bir grafikte yaklaşık olarak doğrusal görünerek) Zipf yasasına uygunluklarını göstermiştir.^[8]

Vitold Belevitch ise çok sayıda iyice belirtilebilen istatistiksel dağılımı (sadece normal dağılımı değil) ele alıp bunların bir sıralamasını yapmıştır. Sonra her bir ifadeyi bir Taylor serisi olarak genişletmiştir. Çok dikkat çekici bir sonuç olarak incelendiği her halde elde edilen Taylor serisinin birinci-sıra kesiminin Zipf Yasası'na ve ikinci-sıra kesiminin ise Zipf-Mandelbrot Yasası'na uygun oldukları görülmektedir.^[9][10]

Zipf'in şahsi açıklaması belirlenmiş bir insan dilini konuşanların ve bu dille yazarların ifade ettiklerinin anlaşılabilmesi için yaklaşık olarak eşit dağılımlı efor sarf etmekten fazla uğraşmaktan sakınmaktadırlar. Bu gereken eforun fazlasından kaçınmak Zipf Yasası'nın gözlenmesine neden olmaktadır.^[11]

Ayrıca bakınız

• Bradford yasası
• Demographic gravitation
• Sıklılık listesi
• Heaps yasası
• Lorenz eğrisi
• Lotka yasasi
• Pareto dağılımı
• Pareto prensibi, yani, "80-20 kuralı"
• Sıralama büyüklüğü dağılımı

Notlar

1. Zipf George K. (1935). The psychology of language.Cambridge, Mass.: Houghton-Mifflin.
2. Zipf George K. (1949). Human behavior and the principle of least effort. Addison-Wesley.
3. Auerbach F (1913) Das Gesetz der Bevölkerungskonzentration. Petermanns Geogr Mitt 59: 74–76
4. Christopher D. Manning, Hinrich Schütze Foundations of Statistical Natural Language Processing, MIT Press (1999), ISBN 978-0-262-13360-9, say. 24
5. Brillouin, Léon [1959] 2004. La science et la théorie de l'information.
6. Eeckhout J. (2004), "Gibrat's law for (All) Cities." American Economic Review C.94(5), say.1429-1451.
7. Adamic, Lada A. "Zıpf, Üstel-yasalar ve Pareto - bir sıralama ders notu"
8. Li, Wentian (1992). "Random Texts Exhibit Zıpf's-Law-Like Word Frequency Distribution". İEEE Transactions on Information Theory 38: 1842–1845. DOI:10.1109/18.165464. 
9. Belevitch, Vitold (1959), "On the statistical laws of linguistic distributions", Annales de la Soçiété Scientifique de Bruxelles C.73 seri İ say.310-326.
10. "Statistical metalinguistics and Zıpf/Pareto/Mandelbrot" SRİ International Computer Science Laboratory, erişim: archived 29 Mayıs 2011.
11. Zıpf, George K. 1969) Human Behavior and the Principle of Least Effort", Cambridge, Mass, Addison-Wesley,s.1

Dış bağlantılar

• Zipf, George K. (1949) Human Behavior and the Principle of Least Effort. Cambridge, Mass.:Addison-Wesley. (İngilizce)
• Zipf, George K. (1935) The Psychobiology of Language. Houghton-Mifflin. (İngilizce)
• Gutenberg projesi için İngilizce, Fransizca, İspanyolca, İtalyanca, Isveçce, Izlandaca, Latince, Portekizce ve Fince dilleri için Zipf semantik derinlik listesi. Herhangi bir yazılı metin için "online" hesaplama programı
• Zipf yasası için kapsamlı bibliyografya
• Zipf yasası için PlanetMath maddesi
• Fransizca sözcükler için Zipf Listesi
• Wolfram Projesi için A.B.D. şehirleri için Zipf Yasası. Hazırlayan: Fiona Maclachlan