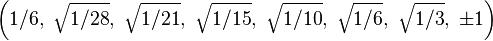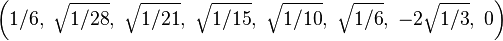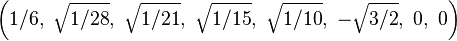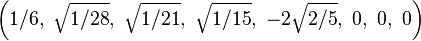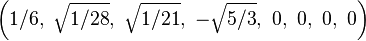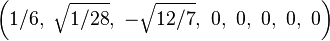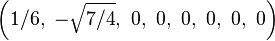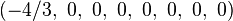8-simpleks

Düzenli enneazetton (8-simplex)
Ortogonal izdüşüm Petrie poligonu içinde
Tip	Düzenli 8-politop
Aile	simpleks
Schläfli sembolü	{3,3,3,3,3,3,3}
Coxeter-Dynkin diyagramı
7-yüzler	9 7-simpleks
6-yüzler	36 6-simpleks
5-yüzler	84 5-simpleks
4-yüzler	126 5-hücre
Hücreler	126 dörtyüzlü
Yüzler	84 üçgen
Kenarlar	36
Köşeler	9
Tepe figürü	7-simplex
Petrie poligonü	enneagon
Coxeter group	A8 [3,3,3,3,3,3,3]
Dual	Self-dual
Properties	konveks

geometride,bir 8-simpleks kendinden-dual düzenli 8-politoptur. Onun has 9 köşeleri var, 36 kenarlar, 84 üçgen yüzler, 126 dörtyüzlü hücreler, 126 5-hücre 4-yüzler, 84 5-simpleks 5-yüzler, 36 6-simpleks 6-yüzler, ve 9 7-simpleks 7-yüzler. Onu ikiyüzlü açılar is cos⁻¹(1/8)dir, veya aşağı yukarı 82.82°.

Ona bir enneazetton, veyaennea-8-topedenebilir,8-boyutlar içinde bir 9-yontulmuş politop olarak .. name enneazetton enneadan türetilmitir Grekçede dokuz yüzeyler için ve -zetta için yedi-boyutlu yüzeyler var, ve -ol.

Koordinatlar

Bir origin-merkezli köşelerinin Kartezyen koordinatları düzenli enneazetton var kenar uzunluğu length 2 dir:

$\left(1/6,\ \sqrt{1/28},\ \sqrt{1/21},\ \sqrt{1/15},\ \sqrt{1/10},\ \sqrt{1/6},\ \sqrt{1/3},\ \pm1\right)$

$\left(1/6,\ \sqrt{1/28},\ \sqrt{1/21},\ \sqrt{1/15},\ \sqrt{1/10},\ \sqrt{1/6},\ -2\sqrt{1/3},\ 0\right)$

$\left(1/6,\ \sqrt{1/28},\ \sqrt{1/21},\ \sqrt{1/15},\ \sqrt{1/10},\ -\sqrt{3/2},\ 0,\ 0\right)$

$\left(1/6,\ \sqrt{1/28},\ \sqrt{1/21},\ \sqrt{1/15},\ -2\sqrt{2/5},\ 0,\ 0,\ 0\right)$

$\left(1/6,\ \sqrt{1/28},\ \sqrt{1/21},\ -\sqrt{5/3},\ 0,\ 0,\ 0,\ 0\right)$

$\left(1/6,\ \sqrt{1/28},\ -\sqrt{12/7},\ 0,\ 0,\ 0,\ 0,\ 0\right)$

$\left(1/6,\ -\sqrt{7/4},\ 0,\ 0,\ 0,\ 0,\ 0,\ 0\right)$

$\left(-4/3,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0\right)$

Daha basitçe, 8-simpleksin köşeleri (0,0,0,0,0,0,0,0,1)ın permütasyonları olarak 9-uzay içinde pozisyon alabilir. Bu yapı 9-ortopleksin yüzeyleri olarak tabandır.

Görüntüler

Şablon:8-simplex Coxeter plane graphs

İlişkili politoplar ve balpeteği

Bu politop ve bir tektip tessellationlar içinde bir yüz: 2₅₁,ve 5₂₁ ile sıralıCoxeter-Dynkin diyagramdır:

,

Bu politop 135 tektip 8-politoplar ile A₈ simetridir. Şablon:Enneazetton family

Kaynakça

• H.S.M. Coxeter:
  • Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
  • H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973, p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
  • Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
    • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
    • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26. pp. 409: Hemicubes: 1_n1)
• Norman Johnson Uniform Polytopes, Manuscript (1991)
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
• Şablon:KlitzingPolytopes

Dış bağlantılar

• Şablon:PolyCell
• Polytopes of Various Dimensions
• Multi-dimensional Glossary

Şablon:Polytopes