Eğrisel koordinatlar

daha genel matematiksel detay için özel (ve önemli) durum için ortogonal koordinatlar, ve eğrisel koordinatlardaki tensorler'e bakınız .

eğrisel, affine, ve kartezyen iki-boyutlu uzay içideki koordinatlar

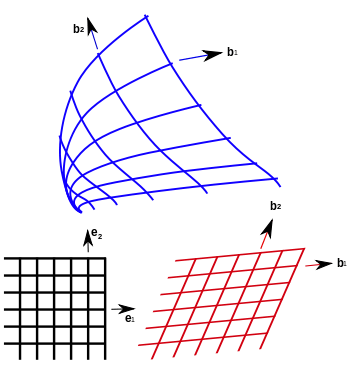
Geometride,koordinat çizgileri eğimli Öklid uzayı içinde eğrisel koordinatların olduğu bir koordinat sistemi vardır. Bu koordinatlar her noktada yerel ters bir dönüşüm ( bire-bir Harita ) kullanarak Kartezyen koordinatları bir dizi elde edilebilir . Bu biri kendi eğrisel koordinatlar ve arkasına bir Kartezyen koordinat sisteminde verilen bir nokta dönüştürmek anlamına gelir . eğrisel koordinatlar adı Fransız matematikçi Lamé tarafından icat edildi,eğrisel sistemlerinin koordinatyüzeyi kavisli olduğu gerçeğinden kaynaklanmaktadır . Üç boyutlu Öklid uzayında (R³) olarak eğrisel koordinat sistemlerinin iyi bilinen örnekleri , kartezyen, silindirik ve küresel polar koordinatlar . Bu alanda bir koordinat yüzeyi bir düzlemdir , örneğin z = 0 , x-y düzlemi tanımlar . Aynı alanda , küresel kutupsal koordinatlarda koordinat yüzey r = 1 kavisli birim küre , bir yüzeydir. Eğrisel koordinatları gösterimi standart koordinat sistemleri birleşik ve genel bir açıklama sunar . Eğrisel koordinatlar genellikle , örneğin, skaler , vektör ya da tensor olabilir fiziksel büyüklüklerin yeri veya dağıtım tanımlamak için kullanılır . vektör hesabı ve tensor analizi (such as the gradient, diverjans, curl, ve Laplasien)) bu miktarlar içeren matematiksel ifadeler skaler büyüklükler, vektörler ve tensörler için dönüşüm kurallarına göre , bir koordinat sisteminden diğerine dönüştürülebilir. Bu ifadeler daha sonra herhangi bir eğrisel koordinat sistemi için geçerli olur. Uygulamaya bağlı olarak, bir eğri şekilli koordinat sistemi Kartezyen koordinat sistemine göre kullanımı daha kolay olabilir. Örneğin,R³te, tanımlanan küresel simetri'ye genellikle Kartezyen koordinatlarındaki fiziksel(örneğin ,merkezi güç etkisi altında hareket parçacıkları ), bir sorunu küresel polar koordinat içinde çözmek için daha kolaydır. Belirli bir eğrisel koordinat sistemi için koordinat yüzeyleri takip sınır koşulları ile denklem bu sistemde çözmek daha kolay olabilir . Biri bir yörüngede bir parçacık için küresel koordinatlarda tercih ise bir örneği için , Kartezyen koordinatlarda dikdörtgen bir kutu içinde bir parçacığın hareketini tarif edersiniz . Küresel koordinatlar yer bilimleri, kartografi, and fizik ( kuantum mekaniği, görelilik) ) , ve mühendislik gibi alanlarda en çok kullanılan eğrisel koordinat sistemlerinden biridir.

3d içinde ortogonal eğrisel koordinatlar

Üç boyutlu bir kovaryant olarak oluşturma

aynı 2 boyutta olduğu gibi, b₁ gösterilebilir

${\displaystyle \mathbf {b} _{1}=p^{1}\mathbf {e} _{1}+p^{2}\mathbf {e} _{2}+p^{3}\mathbf {e} _{3}={\cfrac {\partial x_{1}}{\partial q^{1}}}\mathbf {e} _{1}+{\cfrac {\partial x_{2}}{\partial q^{1}}}\mathbf {e} _{2}+{\cfrac {\partial x_{3}}{\partial q^{1}}}\mathbf {e} _{3}}$

Benzer denklemler için b₂ ve b₃ böylece standart olarak {e₁, e₂, e₃} yerele dönüştürülür.(yerine ve normalize) taban {b₁, b₂, b₃} Aşağıdaki denklemler sistemi tarafından:

${\displaystyle {\begin{aligned}\mathbf {b} _{1}&={\cfrac {\partial x_{1}}{\partial q^{1}}}\mathbf {e} _{1}+{\cfrac {\partial x_{2}}{\partial q^{1}}}\mathbf {e} _{2}+{\cfrac {\partial x_{3}}{\partial q^{1}}}\mathbf {e} _{3}\\\mathbf {b} _{2}&={\cfrac {\partial x_{1}}{\partial q^{2}}}\mathbf {e} _{1}+{\cfrac {\partial x_{2}}{\partial q^{2}}}\mathbf {e} _{2}+{\cfrac {\partial x_{3}}{\partial q^{2}}}\mathbf {e} _{3}\\\mathbf {b} _{3}&={\cfrac {\partial x_{1}}{\partial q^{3}}}\mathbf {e} _{1}+{\cfrac {\partial x_{2}}{\partial q^{3}}}\mathbf {e} _{2}+{\cfrac {\partial x_{3}}{\partial q^{3}}}\mathbf {e} _{3}\end{aligned}}}$

Benzer akıl yürütme olarak, bir yerel bazdan, standart baza ters dönüşüm elde edebiliriz

${\displaystyle {\begin{aligned}\mathbf {e} _{1}&={\cfrac {\partial q^{1}}{\partial x_{1}}}\mathbf {b} _{1}+{\cfrac {\partial q^{2}}{\partial x_{1}}}\mathbf {b} _{2}+{\cfrac {\partial q^{3}}{\partial x_{1}}}\mathbf {b} _{3}\\\mathbf {e} _{2}&={\cfrac {\partial q^{1}}{\partial x_{2}}}\mathbf {b} _{1}+{\cfrac {\partial q^{2}}{\partial x_{2}}}\mathbf {b} _{2}+{\cfrac {\partial q^{3}}{\partial x_{2}}}\mathbf {b} _{3}\\\mathbf {e} _{3}&={\cfrac {\partial q^{1}}{\partial x_{3}}}\mathbf {b} _{1}+{\cfrac {\partial q^{2}}{\partial x_{3}}}\mathbf {b} _{2}+{\cfrac {\partial q^{3}}{\partial x_{3}}}\mathbf {b} _{3}\end{aligned}}}$

Jacobian dönüşüm

Lineer denklem sistemleri matris formunda yazılabilir

${\displaystyle {\cfrac {\partial x_{i}}{\partial q^{k}}}\mathbf {e} _{i}=\mathbf {b} _{k},\quad {\cfrac {\partial q^{i}}{\partial x_{k}}}\mathbf {b} _{i}=\mathbf {e} _{k}}$.

Bu lineer sistemin katsayı matris Jacobian matris'in (ve tersidir) dönüşümüdür.Bu denlemler bir Kartezyen tabanı bir eğrisel tabana dönüştümek için kullanılabilir, veya tam tersi.

Üç boyut içinde, bu matrislerin genişletilmiş formu

${\displaystyle \mathbf {J} ={\begin{bmatrix}{\cfrac {\partial x_{1}}{\partial q^{1}}}&{\cfrac {\partial x_{1}}{\partial q^{2}}}&{\cfrac {\partial x_{1}}{\partial q^{3}}}\\{\cfrac {\partial x_{2}}{\partial q^{1}}}&{\cfrac {\partial x_{2}}{\partial q^{2}}}&{\cfrac {\partial x_{2}}{\partial q^{3}}}\\{\cfrac {\partial x_{3}}{\partial q^{1}}}&{\cfrac {\partial x_{3}}{\partial q^{2}}}&{\cfrac {\partial x_{3}}{\partial q^{3}}}\\\end{bmatrix}},\quad \mathbf {J} ^{-1}={\begin{bmatrix}{\cfrac {\partial q^{1}}{\partial x_{1}}}&{\cfrac {\partial q^{1}}{\partial x_{2}}}&{\cfrac {\partial q^{1}}{\partial x_{3}}}\\{\cfrac {\partial q^{2}}{\partial x_{1}}}&{\cfrac {\partial q^{2}}{\partial x_{2}}}&{\cfrac {\partial q^{2}}{\partial x_{3}}}\\{\cfrac {\partial q^{3}}{\partial x_{1}}}&{\cfrac {\partial q^{3}}{\partial x_{2}}}&{\cfrac {\partial q^{3}}{\partial x_{3}}}\\\end{bmatrix}}}$

Ters dönüşüm (ikinci denklem sisteminin), bilinmeyenler eğrisel olarak vektörlerdir. Tüm noktaları için sadece bir ve temel vektörlerin yalnızca bir kümesi (başka hiçbir vektör bu noktalarda tanımlanmamış) orada var olabilir. Bu durumun lineer cebir'de tatmin edici,ancak ve ancak denklem sisteminde tek bir çözüm vardır,kendi sistemini matris belirleyicisi sıfırdan farklı ve yalnızca bir lineer denklem sistemi tek bir çözüm (Önemsiz olmayan) vardır:

${\displaystyle \det(\mathbf {J} ^{-1})\neq 0}$

arkasındaki mantığı gösteren gereksinimi ters Jacobian determinant belirliyor.

n boyutun genellemesi

Christoffel sembolü

Christoffel sembolü nün ilk türü

${\displaystyle \mathbf {b} _{i,j}={\frac {\partial \mathbf {b} _{i}}{\partial q^{j}}}=\Gamma _{ijk}\mathbf {b} ^{k}\quad \Rightarrow \quad \mathbf {b} _{i,j}\cdot \mathbf {b} _{k}=\Gamma _{ijk}}$

Burada virgül bir kısmi türev gösterir (bkz Ricci hesabı).Bunu ifade etmek için Γ_ijk içindeki terimlere g_ij dikkat edilirse

${\displaystyle {\begin{aligned}g_{ij,k}&=(\mathbf {b} _{i}\cdot \mathbf {b} _{j})_{,k}=\mathbf {b} _{i,k}\cdot \mathbf {b} _{j}+\mathbf {b} _{i}\cdot \mathbf {b} _{j,k}=\Gamma _{ikj}+\Gamma _{jki}\\g_{ik,j}&=(\mathbf {b} _{i}\cdot \mathbf {b} _{k})_{,j}=\mathbf {b} _{i,j}\cdot \mathbf {b} _{k}+\mathbf {b} _{i}\cdot \mathbf {b} _{k,j}=\Gamma _{ijk}+\Gamma _{kji}\\g_{jk,i}&=(\mathbf {b} _{j}\cdot \mathbf {b} _{k})_{,i}=\mathbf {b} _{j,i}\cdot \mathbf {b} _{k}+\mathbf {b} _{j}\cdot \mathbf {b} _{k,i}=\Gamma _{jik}+\Gamma _{kij}\end{aligned}}}$

ile

${\displaystyle \mathbf {b} _{i,j}=\mathbf {b} _{j,i}\quad \Rightarrow \quad \Gamma _{ijk}=\Gamma _{jik}}$

Yukarıdaki ilişkileri kullanarak yeniden düzenleme şunu verir

${\displaystyle \Gamma _{ijk}={\frac {1}{2}}(g_{ik,j}+g_{jk,i}-g_{ij,k})={\frac {1}{2}}[(\mathbf {b} _{i}\cdot \mathbf {b} _{k})_{,j}+(\mathbf {b} _{j}\cdot \mathbf {b} _{k})_{,i}-(\mathbf {b} _{i}\cdot \mathbf {b} _{j})_{,k}]}$

Christoffel sembolü'nün ikinci türü

${\displaystyle \Gamma _{ij}{}^{k}=\Gamma _{ji}{}^{k},\quad {\cfrac {\partial \mathbf {b} _{i}}{\partial q^{j}}}=\Gamma _{ij}{}^{k}\mathbf {b} _{k}}$

Bunun anlamı

${\displaystyle \Gamma _{ij}{}^{k}={\cfrac {\partial \mathbf {b} _{i}}{\partial q^{j}}}\cdot \mathbf {b} ^{k}=-\mathbf {b} _{i}\cdot {\cfrac {\partial \mathbf {b} ^{k}}{\partial q^{j}}}}$

Diğer ilişki aşağıdadır

${\displaystyle {\cfrac {\partial \mathbf {b} ^{i}}{\partial q^{j}}}=-\Gamma ^{i}{}_{jk}\mathbf {b} ^{k},\quad {\boldsymbol {\nabla }}\mathbf {b} _{i}=\Gamma _{ij}{}^{k}\mathbf {b} _{k}\otimes \mathbf {b} ^{j},\quad {\boldsymbol {\nabla }}\mathbf {b} ^{i}=-\Gamma _{jk}{}^{i}\mathbf {b} ^{k}\otimes \mathbf {b} ^{j}}$

Bakınız

• Kovaryans ve kontrvaryans
• Eğri uzay-zamanın matematiğine Temel giriş
• Ortogonal koordinatlar
• Frenet–Serret formülü
• Kovaryant türev
• Tensör türevi(mekanik süreklilik)
• Eğrisel çerçeve
• Silindirik ve küresel koordinatlarda del

Kaynakça

Daha fazla bilgi

• Spiegel, M. R. (1959). Vector Analysis. New York: Schaum's Outline Series. ISBN 0-07-084378-3. 
• Arfken, George (1995). Mathematical Methods for Physicists. Academic Press. ISBN 0-12-059877-9. 

Dış bağlantılar

• Derivation of Unit Vectors in Curvilinear Coordinates
• MathWorld's page on Curvilinear Coordinates
• Prof. R. Brannon's E-Book on Curvilinear Coordinates
• – Wikiversity, Introduction to Elasticity/Tensors.

Şablon:Orthogonal coordinate systems